新着情報
牛深ハイヤ大橋のボーリング資料採取【科学部】
1月11日(土)、牛深支所の橋口様のご協力を得て、牛深ハイヤ大橋建設の際に掘削されたボーリングコアから試料を採取しました。
これをもとに、天草西岸の海水準変動を調査します。
天草の方々の温かいご支援を得て、研究が発展していることに、心より感謝いたします。
橋口様、ありがとうございました。

第4回天草サイエンスアカデミー開催【小中学生向け科学講座】
12月26日(木)、天草高校において第4回天草サイエンスアカデミーを開催しました。
これは、小中学生に向けた科学講座で、2年ASクラスの生徒が企画し実施するものです。
また、2年生有志が、運営をサポートしてくれました。
今回は7講座を2回ずつ開講し、200名を越える小中学生に科学の面白さを伝えました。
①キラキラ氷の結晶を作ろう!
②世界に一つだけの空気砲を作ろう!
③これで君も力持ち!? (動滑車の仕組み)
④シャボン玉のふしぎ
⑤プログラミング
⑥顕微鏡でケイソウを見てみよう!
⑦VRを体験しよう!
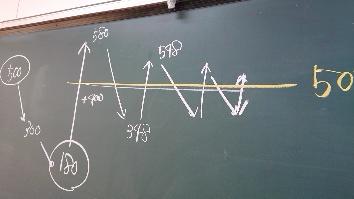
数科学探究Ⅰ 「薬の体内残量と服用量の関係②」
12月23日(月)の数科学探究Ⅰです。
前回に引き続き、薬の体内残量問題です。
一日薬を飲み忘れた人が、次の日に2倍の薬を飲んでもよいのかということを、数学的に考察し、記述文でまとめました。
テキストはこちら → https://sh.higo.ed.jp/amakusa/SSH/text
Skypeで土坪高校の日本語発表大会観覧
12月20日(金)、土坪高校の日本語発表大会をSkypeで観覧しました。
夢や愛犬、翻訳について思うこと、韓国の城の紹介など、土坪高校生が興味・関心のある話題がテーマでした。
また、天高生との交流を話してくれた生徒がいて、聞いていた生徒が感動していました。
最後に、天草高校の生徒たちから、クリスマスメドレーをプレゼントしました。

ASⅡ 研究の様子
12月19日(木)のASⅡです。
今年最後です。
それぞれの研究計画にそって、研究活動を進めました。
AMAKUSA KAERU.labの富崎様にも助言を頂きました。