【数科学探究Ⅱ】缶詰めの考察①
投稿日時 : 2021/06/24
各部担当者
各部担当者
6月24日(木)の数科学探究Ⅱです。
缶詰の容積と表面積の関係を考察します。
例えば、容量(100mlなど)の商品を、円柱状の缶詰めにして販売するとします。
そのとき、缶詰めの入れ物にかかるコストを最も安く抑えたいと思うはずです。
これを数学的に考えると、缶詰めの表面積を最小にしたいということになります。
そこで、数学Ⅲで履修した微分法を活用して、そのような条件が最適かを考察しました。
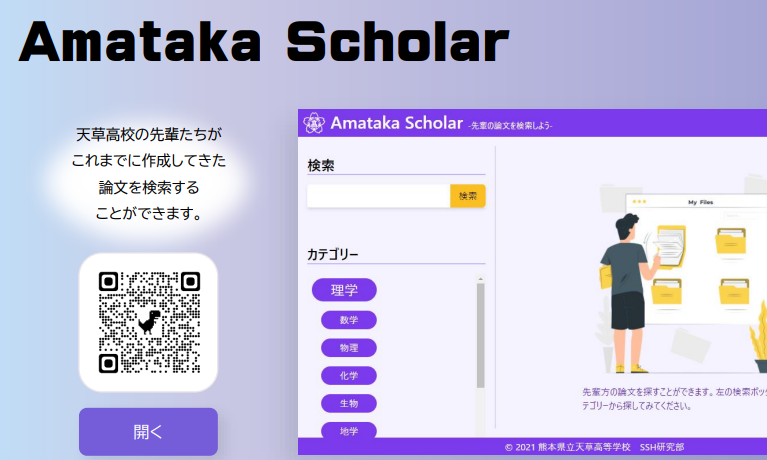
■ テキストはこちら → https://sh.higo.ed.jp/amakusa/SSH/text
