徒然雑記帖
明日から期末テスト
いつも本校のHPにお越しいただきありありがとうございます。
また月曜日が始まりました。梅雨の中休みでしょうか、朝から青空が広がって気持ちがいい一日です。

今日は私たち教職員の完全定時退勤日に合わせて、生徒の皆さんたちも部活動がない日になります。さっさと下校して、ラケットやバットを鉛筆に持ち替えて、しっかり勉強に励んでください。
勉強に疲れたら夜空を見上げてみてみるといいかもしれません。左側がちょっと欠けた大きな月がぽっかりと浮かんでいることでしょう。淡い月の光が目を優しく癒やしてくれるはずです。満月は3日後の6月28日(木)です。
ところで、「最近アクセス数を話材にした記事が最近出ていませんね」と、私自身も気にしていたことについて、何人かの先生方から声をかけていただいています。
今年、4月6日に6桁から7桁へと1桁あがり100万台になりました。100万に達した後は(およそ1週間後に110万になりそうではありますが)、なかなか興味をひく数字が出現しなかったことによるものです。
本日6月25日16時25分現在の総アクセス件数は、1095470 です。正直、食指が動く数字ではありませんが、久々にやってみます。(数字の並びをそのままにして、加減乗除等の記号を入れて、今日の日付である625を作ってみます)
1095-470=625 → 6月25日
あっという間に立式できましたが、全く面白みがありません。もう一ひねりしてみます。
(1+0!)9+5!-4-[√7]―0!=625 → 6月25日
【注】 中学生の皆さんへ !は「階乗」または「ファクトリアル」と読み、詳しいことは高校の数学で学習します。ここにある5!なら、5×4×3×2×1を計算して120になります。このようにn!なら、n×(n-1)×…×3×2×1の自然数の積を計算します。そして、0!(ゼロの階乗)は1です。これは約束(決め事)ですから、「どうしてそうなるの?」とか考えたらいけません。
この式にはもう一つ見慣れない記号([ ])があります。これはガウス記号と呼ばれ、その数を超えない最大の整数を表す記号です。私の記事では初めて登場する数学の記号になりますが、そんなに難しくはありません。例えば[3.14]=3になりますし、[-0.23]=-1となります。
従って、上の式では√7≒2.645・・・ですから、[√7]=2です。
数学の先生に聞いたところ、ガウス記号は教科書に載っていないので、本校では扱ってないそうですが、教科書に載っていなくても『実数xを超えない最大の整数を[x]と表すこととする』という注意書きを問題文に明示したうえで、大学入試には出題されていますので注意が必要です。就職試験でも前述の [-0.23] =? 程度の問題でしたが、出題されていたのを受検報告書で見た覚えがあります。
ちなみにガウスは、19世紀のドイツの超天才数学者・物理学者です。彼の業績は極めて多岐に渡り、数学や電磁気などの物理学で彼の名を冠した定理や法則が多数存在するんだそうです。
話は大きく変わって、朝のテレビで言っていたことになります。本日、6月25日は、1960年(昭和35年)の今日、自動車による交通が発達し、道路における危険の防止と交通の安全と円滑、道路交通による障害の防止を目的とした「道路交通法」が施行された日なんだそうです。
道路交通法と聞いて、私たち教職員がいつも気をつけておかなければならないことは、「第65条第1項 何人も*、酒気を帯びて車両等を運転してはならない」だと強く思っています。
* 法律解説書の注釈には、「何人」というのは、運転免許を受けている人にかかわらず、全ての人が対象で、車両等とは、自動車はもちろん、電車や軽車両等(自転車等)までを含むとありました。
先月、熊本市で自転車に乗って登校していた高校3年生の女子生徒が酒気帯び運転の人が運転するワゴン車にはねられて死亡するという大変痛ましい事故がありました。どんなに気をつけていても飲酒運転のクルマに巻き込まれたらどうしようもなく、この報に接して大きな無力感を感じました。
生徒の皆さんたちも、もうすぐクルマの運転免許証を手にするはずです。お互いに良き交通社会人でありたいものです。
【校長】
サイン・コサイン何になる・・・♪
公開授業週間の今週、2年生の各教室では、数学で三角関数の加法定理をやっています。「ここって苦労する所なんだよな・・・」と、自分自身も三角関数に手を焼いていた高校時代を思い出しました。
自分が数学教師だったら入門程度の三角関数の範囲でどんな問題を出すだろう・・・と、10問作問してみました。
生徒の皆さん、三択式ですからよかったら解いてみてください。
一部おふざけの問題も入ってますので、あくまでも暇つぶしにどうぞ。
でも、1問20秒のペースで解いていって、7問以上正解だったら、「三角関数検定3級」位の力はあるのでは?と思います。
1 三角関数で、sinは日本語で「正弦」といいますが、cosは何という?
①余接 ②正接 ③余弦
2 三角関数の主役、sinさん、cosくん、tanさんのうち、いつも自虐的にひがんでいると思われるのは誰?
①sinさん ②cosくん ③tanさん
3 アンケートで「三角関数が嫌い」と答えた日本の高校生が、その理由として挙げた中でいつも最上位にあるものは?
① 公式が多い。
② 三角関係を思い出して苦しくなるから。
③ sin、cos、tanとの出会いが「超唐突!!」で「何、コイツら?」の思いをずっと引きずってしまったから
4 三角関数のイロハともいえる三角比(三角形、特に直角三角形の辺の比を考える分野)は、いつ頃どこで産声をあげた?
① 紀元前約2000年頃のエジプト
② 紀元前約200年頃のギリシャ
③ 1740年頃のスイス
①0.016° ②0.16° ③1.6°
6 次の角度のうち、sinとcosの値が等しくなるのは?
①135° ②225° ③315°
7 sin75° と sin30°+sin45°の大小関係は?
①sin75°>(sin30°+sin45°)
②sin75°=(sin30°+sin45°)
③sin75°<(sin30°+sin45°)
8 中学校で習った「三平方の定理」というのは、【 】定理の特別な場合(θ=90°の場合)だった。
①正弦 ②余弦 ③正接
9 次の勉強嫌いの生徒のほざきに、教師になったつもりで力強く論破してください。一番説得力のあるものは?
「何でcos135°を求める必要があんの?やってる意味ねぇし、人生に三角関数なんか必要ねぇし」
① 三角関数が必要な職業が選べなくなり、人生の選択肢を狭めてしまうよ!
② 私は今その三角関数を君たちに教えることでお金をもらってま~す。
③ 「何の役に立つの?」って疑問は「そもそも何で必要なの?」って疑問なわけで、その答えは「じゃあ、あんた何で生まれたの?」に帰結するよ!
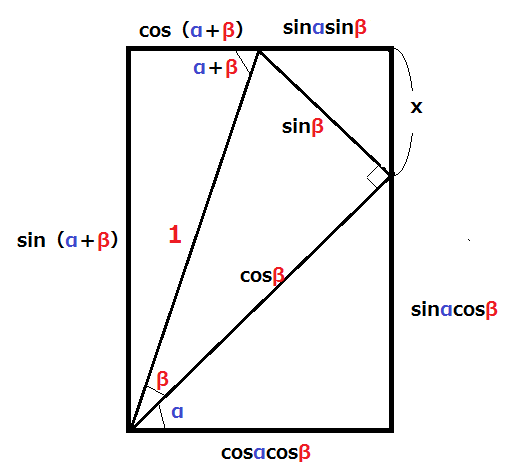
xに相当する長さは?
①cosβsinα
②sinβcosα
③cosαsinβ
【答え】
1:③ 2:③ 3:① 4:① 5:②
6:② 7:③ 8:② 9:①②③(どれを選んでも正解) 10:③
【解説】
1: 数学Ⅰの教科書で確認してください。
既に習ったように、sin(サイン)とcos(コサイン)の間には、sin2θ+cos2θ=1(サインの2乗とコサインの2乗の和は1)という強力な関係があります。その意味で「サインとコサインは一対」であると言っても過言でありません。コサインの英語表記cosineは、co+sineでco-は「~と共に」という意味を作る接頭辞です。なるほど、コサイン(cos)はサイン(sin)と常に共にあるので、この英語表記は分かりやすいです。しかし、日本語になるとcosがなぜ「余弦」と名付けられたのか?
「余」に込められた意味等を追究してみるのも一興かもしれません。
2: 次のサイトを見てみてください。tanさんの嘆きが聞こえてきそうです。
http://nlab.itmedia.co.jp/nl/articles/1710/18/news049.html
数学Ⅰでよく出題される三角関数の式の証明では、tanΘが出てきたらsinΘ/cosΘに直して計算すればうまくいくことが多いです。でも、とかく分数の計算はややっこしくなりがちで、tanΘを見ると「うわ…」と引かれる原因なのかもしれません。
A+B+C=π のとき、tanA+tanB+tanC=tanAtanBtanCなんていう美しい公式もあります。tanさんの良いところを見つけて、エールを送ってください。
3: あるアンケート(自由記述)で②の回答を見たとき笑ってしまいました。
私、三角関数ほど単純なものはなく、三角関係ほど複雑なものはないと思うのですが・・・。
皆さん方が学習してきたように、三角関数はまず直角三角形による定義をしますが、次に単位円による定義に拡張されます。その拡張された定義の元では三角関数は「円関数」と呼ばれることもあります。従って、三角関数からどうしても三角関係を連想される方は、「円関数!!」と5回ほど唱えれば邪念が払われるかもしれません?
4: これは数学史の問題です。その手の本を紐解くと、①の紀元前 2000 年頃、エジプト人がピラミッドの建設で原始的な三角比(1年の最初の頃に習った三角関数)を使っていたとあります。
そして、今2年生の皆さんが習っている三角関数や加法定理は、②の古代ギリシャ時代には確立されていたというので驚きです。
なお、③の1740年ごろというのは、オイラーが次の公式を発見した記念すべき年です。
ei x=cosx+ isinx
実数の世界では全くの無関係のように思われていた指数関数と三角関数が、複素数の世界では親戚どころか兄弟であったことを意味する重要な式です。
この式は、大学の工学部や理学部等に進学すると数学で学びます。今の段階ではこんな式があるんだ・・・という理解で十分です。オイラーはスイス生まれの数学者で、人類史上最も多くの論文を書いた数学者であったと言われています。
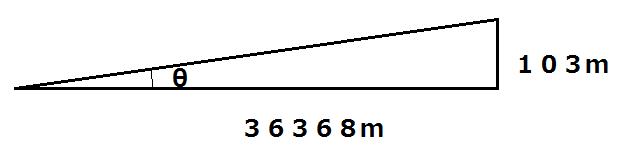
5: これは直感で正解してほしいところですが、ある意味難問かもしれません。
実際、人吉から八代方面に向かって国道219号線を車に乗っていると、道がずっとゆるやかな下り坂になっていることに気付くはずです。一体どのくらいの勾配なんでしょう?
これは、逆三角関数と呼ばれる計算をすることで求めることができます。
逆三角関数は数学では習っていないと思いますが、設計などの専門科目で学びますし、計算技術検定2級を受検した人にはおなじみのはずです。
Θ=tan-1(103/36368)を関数電卓に入れると、約0.16と表示されます。
6: 三角関数を単位円で再定義した際に、sinはy座標、cosはx座標になります。従って、第1象限と第3象限でsinとcosが等しくなることがありえます。
ちなみにこの問題は競技クイズ日本一決定戦の予選第1回戦(1問平均10秒のペースで解答する力が要求)に出題されました。
7: 頭の中に単位円を描き、30°、45°、75°それぞれのy座標をイメージしてください。30°のy座標と45°のy座標を重ね合わせた(足し合わせた)高さと75°の高さの比較になります。頭の中に図が丁寧に描ければ答は自ずと③と分かるはずです。
ここでは計算で求めてみます。
sin30°=1/2(=0.5)、sin45°=√2/2です。
ここで√2を約1.4として計算すると右辺は、
sin30°+sin45°=0.5+0.7=1.2
では、左辺のsin75°はいくらでしょう?
既に「加法定理」を学習した皆さんなら簡単です。
sin(α+β)=sinαcosβ+cosαsinβを使って
sin75°=sin(45°+30°)
=sin45°cos30°+cos45°sin30°
=(√2/2)( √3/2)+(√2/2)( 1/2)
=(√6+√2)/4
ここで、先ほどと同様に、√6を約2.4、√2を約1.4として計算すると、
sin75°=(√6 + √2)/4=(2.4+1.4)/4=3.8/4=0.95
従ってsin75°<(sin30°+sin45°)となります。
ここで覚えておいてほしいのは、
sin(α+β)=sinαcosβ+cosαsinβ
であって、
sin(α+β)=sinα+sinβ
にはならないということです。
では、この問題は加法定理を知らないと解けないのでしょうか?
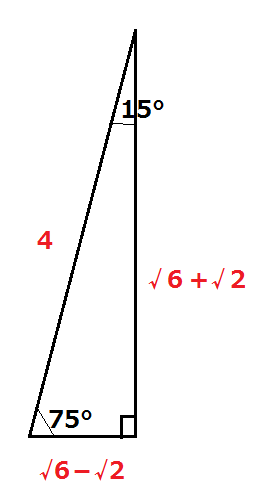
実は、75°と15°の右図のような直角三角形では、辺の比が「 4:√6 + √2:√6 - √2」というのが成り立ちます。
これを覚えておくと15°と75°について、sin、cos、tanの値が図を見ながら、sin75°=(√6 + √2)/4とか、たちどころに分かりますので非常に便利です。
某電力会社の就職試験問題で、sin75°=(□+√2)/4という穴埋め問題で、□に√6を入れさせる問題が出題されたことがあります。加法定理を万一忘れていてもこの辺の比を思い出せば楽勝です。
余談ですが、sinとcosの加法定理そのものの証明が1999年(平成11年)の東京大学の入試で出題されました。「公式は証明してから使うべき」というメッセージなんだろうか、それとも「教科書の内容すら身に付いていないのに難しい問題集を解いている受験生に対する警告」なのだろうかとか色々騒がれました。出来も非常に悪かったそうです。勿論、皆さんは習ったばかりなので証明はバッチリですよね?
8: 余弦定理とは、a2=b2+ c2-2bc・cosAという形の公式です。
今、A=90°のときcos90°=0ですから、a2=b2+ c2となり、これは中学校で習った三平方の定理そのものです。
正弦定理とは、a/sinA = b/sinB = c/sinC という形の公式です。
ちなみに、正接定理と呼ばれているものはありません。
余弦定理を用いることにより、三角形の「2辺の長さとその間の角度」から「残り1辺の長さ」を求められます。また、三角形の「3辺の長さ」が与えられた場合に、すべての角の余弦が求められ、すべての「角の大きさ」を考えることもできます。これに対して、正弦定理は三角形の「1辺の長さ」と「2つの角の大きさ」が与えられた場合に、「残りの2辺の長さ」を求めることができます。慣れるまでどちらの定理を使えばいいのか悩むことがあるかもしれません。
9: これはどれを選んでもマルにします。あなたなら先生からどう言われたいですか?私、自分で解答を作りましたが、3つともとても気にいっています。
この問題の作問のヒントになったのは、「サイン・コサイン何になる・・・♪.」と歌詞の中に出てくる『受験生ブルース』でした。日本のフォークソングの源流を作った男と言われる高石友也の代表曲で、1968年(昭和43年)に大ヒットしました。今でいう「団塊の世代」が大学受験地獄(この言葉は今、死語かも?)を経験していた頃で、当時私は小学3年(9歳)でした。テレビやラジオから毎日のように流れるその哀しい曲を何度も聞いているうちに、サイン・コサインという数学用語がしっかりインプットされました。
高校になって初めてサイン・コサインを習い、「こんなの勉強して何になる?」とその歌詞の意味するところが分かったような気が私自身しましたし、誰でも一度はそう思うのではないかとか考え込んでしまいました。
そういえば、鹿児島県の伊藤祐一郎前知事が2015年(平成27年)8月、「サイン、コサインを女の子に教えて何になる?」などと発言してちょっとした話題になったことがありました。
「いろいろな人生の問題があるため、今の均一な教育の仕組みを変えた方がいい」との思いからの発言だったと釈明されましたが、知事もきっと『受験生ブルース』を聞いて育った世代なのかな・・・と思った次第でした。
私自身も昔、生徒指導部で交通係をしていた頃、多分通学自転車のマナーの悪さに憤慨したドライバーだったんでしょう。苦情の電話の中で「アンタの高校、サイン・コサインとか難しいことを教えなくてもいいから、信号の見方をきちんと指導してくれ!」と罵声を浴びたことがあります。悲しい思い出です。
10: 三角関数はまず直角三角形による定義をします。これはまさにその範囲です。図をよく見ながら丁寧に読み解いていくと必ずわかるはずです。
私は昔からこの図を見るたびに、「本当によく出来た図だな!」と思っていました。あくまでも、α、β、α+βがいずれも鋭角という制限付きではありますが、加法定理がこんなに分かりやすく図の中に表現できるなんて、ある意味凄いです。
是非、sin(α-β)やcos(α-β)が表示できる図も考えてみてください。
【校長】
「ひよどり越え」の名前の由来を探る(その2)
中庭のあじさいの花が二輪咲いています。なぜ紫陽花と書いてアジサイと読むのか知りません。でも、この淡い紫色を見ていると夢見心地の気分にひたれます。
今朝、高校総体の行進の練習がありました。総体が終わるまで梅雨入りは待ってほしいと願っていましたが、とうとう熊本も昨日梅雨入りしてしまいました。
注:以下の記事は、昨年7月20日にアップした「アクセス数682962→鵯(ひよどり)越えの戦い)」の中編になります。(昨年7月20日の記事は→こちら)
本校生が「ひよどり越え」と呼んでいるのは、平家物語の中でも語られる平家滅亡の前兆となる戦い(一ノ谷の戦い)に出てくる呼称です。
いつ頃誰が列車通学生が上ってくるあの坂を「ひよどり越え」と名付けたのか、人吉市史や本校の30周年記念誌などで調べましたが結局分かりませんでした。それどころか意外なことを知りました。それは・・・
「黒坂」
昭和41年4月8日号の人吉新聞に「黒坂の登校階段完成」の見出しに続く次のような趣旨の記述があり、その当時は「黒坂」と呼ばれていたようです。
球磨工業高校通学生徒の一部父兄(主に汽車通学生から市に対し整備を陳情されていた市内城本町の西校登校道路(人吉駅裏の通称黒坂)がこのほどコンクリート階段に整備され、通学生徒をはじめ、地元の利用者は喜んでいる。
同道路は急勾配のため、整備しても一雨降ればすぐ土砂を洗い流し、路面が悪くなり地元民からも整備方が陳情されていた。昨年は悪路を通行する生徒の姿を見て、同町民政委員谷川源昨さんが老身を問わず道路整備に汗を流し生徒から感謝されたこともあったが、今回の整備で通学生も安心して通れると言っている。同道路は延長140m、巾員1mを全長階段にしている。工費は11万6千円。
一方、「大悲坂」とも

そのパンフレットには、「西暦1764年紺屋町の商人達が協力し合い、観蓮寺の観音堂に行く参道を苦労して切り拓き、その事業を後世に残そうと「大悲坂碑」(だいひさかひ)を建てています」とあります。従って、この登り坂は250年前頃は、「大悲坂」と呼ばれていたことになります。

村山観音が安置されているお堂は「大悲殿」と呼ばれているところから来ているのかもしれません。手元の国語辞典によると、「大悲」とは「他人が悲しみ苦しんでいるのをみて助けてあげたいと思う人の心」とあり、どうやら仏教用語のようです。
結局「ひよどり越え」とは?
私、赴任当初から気になっていたことがあります。それは、平家の落人伝説が色濃く残る地域に所在する学校だからある意味当然かもしれませんが、本校も色々と落人伝説と関わりがあるのでは?ということです。どんな点にそれを感じたかと言うと・・・
① 今、話題にしている平家物語にも出てくる「ひよどり越え」のネーミングがまさにそれ。
隣の人吉西小学校の先生方を含め十人近くの行き交う地元の方々に坂道の名前を尋ねてみましたが、その全員が「この坂に名前があるの?」とか「知らない」といった答えばかりでした。人吉西小学校の某先生は、「球磨工生が上がってくる坂」と呼んでいると言われ、「ナルホド!」と思いました。
また、学校評議員をお願いしている1期生の馬場上氏にも尋ねてみたところ、「当時何と呼んでいたか忘れたが、そういう(=ひよどり越え)呼び方はしていなかったはずだ。初めて聞いた」という証言をいただきました。


パンフレットには、「この中の7基の外壁に馬などの動物、武具、文様等の装飾が残っていることから、早くから学界にも注目され、大正10年(1921年)3月3日に国指定史跡となりました。昭和58年から毎年7月第4土曜日には地元城本町住民が中心となって「古墳まつり」が続いています」とありました。
この古墳に沿って、約240人の列車通学生が毎日登下校で使っている365段の階段があり、本校関係者が「ひよどり越え」と名付けているのです。

人吉市に外灯の増設を陳情しても国指定の文化財(大村横穴古墳群)だから形状の変更が難しいらしく、なかなか進んでいないのが現状です。
後編に続きます。
【校長】
Why don’t we go to see a firefly tonight?
いつも本校のHPにお越しいただきありありがとうございます。
朝夕は半袖では少し肌寒いけど、日中は汗ばむ爽やかな初夏の陽気です。そろそろ梅雨入りも気になるところですが、いかがお過ごしでしょうか。
昨日は私たち教師の「完全定時退勤日」ということで、生徒の皆さんは部活がありませんでした。嬉しそうな表情で下校する何人かに「早く帰って何するの?」と水を向けたところ、にこにこしながら異口同音に「勿論、勉強です」と。何かしら可笑しかったです。
私は昨夜8時頃、歩いてコンビニに買い物に行く途中、川べりの草むらに蛍が光を放っているのを目にしました。蛍、今年になって初めてでした。綺麗な清流に恵まれたここ人吉は蛍が舞うんですよね!
昨年、こちらに越してきて、蛍が乱舞する光景を何十年ぶりかに目にして、自然が豊かなんだと改めて驚きました。

そういえば、千年も昔に書かれた「源氏物語」にも、蛍が恋物語にふさわしい感じで描かれています。ズバリ「蛍」と名付けられた巻でです。
手元のシラバスによると、本校の国語では徒然と伊勢は学習しますが、源氏は扱わないみたいですから、生徒の皆さんの中でこのストーリーを知っている方は少ないのかもしれません。ごく大雑把にいうと、玉鬘(たまかずら)という姫君の姿を、ある男性に見せようと考えた光源氏が、暗闇のなかで蛍を放ち、その光に照らし出された姫の美しさに、男性がますます恋心を募らせていくというシチュエーションでした。

暗闇の中のロマンチックな光の明滅に癒されるかもしれません。
【校長】
五月ばかりなどに山里にありく
いつも本校のHPにお越しいただきありありがとうございます。
生徒の皆さん、連休後半をどのように過ごしましたか。
「部活三昧」と聞こえてきそうですが、1日位は休養日があったはずでは・・・?
ということで、私はこどもの日の5日、熊本市の金峰山中腹にある洞窟、霊巌洞*1まで、徒歩で往復(16キロ位)してきました。晩年の5年間を熊本で過ごした宮本武蔵が、この洞窟にこもって兵法書「五輪書(ごりんしょ)」を著したことは、あまりにも有名です。

そんなことを考えていたら、よもぎ餅を久しく口にしていないことを思い出し、どうしても食べたくなって、帰宅後近くのスーパーへ直行。
製菓・パンのコーナーに、最後の1パックが残っていました。某大手パンメーカー製のよもぎ餅大福5個パックで213円。北海道産の粒あん入りです。
そのお味は・・・?
餅の色こそヨモギ色でしたが、その香りはほとんどせず、「こんなものかな・・・」と少し残念でした。夕方のニュースでは温泉施設で「いい香り!」とか言いながら菖蒲湯につかる子どもたちの様子を報じていました。季節の匂いを楽しむ心のゆとりをいつまでも持ちたいものです。
週の初めは大雨です。連休のせいか今週は少し長く感じるかもしれません。高校総体も近づいていますが、あと10日で中間考査。特に、1年生にとっては高校で初めての定期テストになります。ぜひ、計画を立てて学習を始めてください。
*1うっそうと茂る樹木におおわれ、神秘的な霊場として知られる雲巌禅寺(うんがんぜんじ)の裏山に所在します。洞窟内には岩戸観音(いわとかんのん)の名で呼ばれる観音像が安置されています。
*2【口語訳(意訳)】車の車輪に踏まれた蓬が輪が回る時に、ふっと剥がれて車の御簾などに当たり、パシッと微かな音を立てて引っかかるのが趣(おもむき)がある。
【校長】
飛行機雲に想う
いつも本校のHPにお越しいただきありありがとうございます。
月が変わり、いよいよ平成のカウントダウンが始まりました。大型連休狭間の今日5月2日、学校では朝から進学課外の開講式、そして午後はこの春就職して帰省した卒業生を招いて機械科の生徒を対象に進路講話が行われました。
さて、いきなりですが、生徒の皆さんは飛行機に興味がありますか?
私は高校の頃、鉄研(鉄道研究同好会)に所属しており、東京あたりまでの出張なら今でも鉄道を利用するほうで、飛行機は今一つです。でも、お月様を見るのが好きなので、今日はどのあたりにいるんだろうと空を見上げた際に飛行機を見つけることが多々あり、人吉上空を飛ぶ飛行機に興味を持ちました。
多分、上空の気象条件が整った時だと思います。青空の下、一直線にくっきりと力強い雲*1を引く飛行機を目にすることがあり、嫌なことも忘れていつまでも目で追ってしまいます。そうこうしているうちに、人吉上空は、高高度を飛ぶ国際線の旅客機の航路が設定されているのでは?と思うようになりました。
はるか上空を飛ぶ機影を眺めていると、
あれはどこから飛んできてどこに向かっているんだろうとか思いませんか?
私はとても気になります。
知っている人も多いかもしれませんが、リアルタイムで世界中の飛んでいる飛行機が分かるという「Flightradar24」というスマホ用のアプリがあります。今、この瞬間飛んでいる飛行機が、どこを飛んでいて、どんなルートで、高さとスピードはどれぐらいかを地図上に表示してくれるもので、コックピットからの仮想の眺めも見ることができるというものです。(ADS-Bという航空機が現在の位置と高度を絶えず送信するシステムを使っているらしいです)無料版と有料版がありますが、無料版でもインストールしていると結構楽しめるお薦めの神アプリです。
ということで、私、飛行機を見つけると、いつもこのアプリを開いて検索してしまいます。あくまでも私が人吉の空を見上げて確認した飛行機を調べた限りの話になりますが、本市上空を飛ぶ国際線には以下の便がいました。(そのアプリの画像を貼り付けて皆さんにお見せすることができればいいのですが、著作権上その行為が許可されているのかどうか不明ですから、フリーの白地図にいくつかの路線のイメージを書き込んだものを代わりに載せておきます)
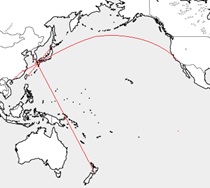
バンコク(タイ)-新千歳、台北-成田、
台北-福岡、マニラ-福岡
仁川(韓国)-グアム、仁川-ウェリントン(ニュージーランド)、
仁川-シドニー(オーストラリア)
上海-サンフランシスコ
重慶(チョンチン:中国)-サンフランシスコ
いかがでしょうか、写真にあったように、人吉上空でいくつかの航路が十字に交わっていることがどういうことかお分かりだと思います。
私は、高校・大学の頃、故城達也さんの素敵な声のナレーションで始まる「ジェットストリーム」*2という深夜ラジオの番組を聴いて育った世代です。だからでしょうか、国際線の飛行機に乗ったことこそ数回しかありませんが、翼のランプを点滅させながら夜間飛行をしている飛行機を眺めると、明日の朝どこに降り立つのだろうかと、この空のもと繋がっている異郷の街や情景を想像してしまい、一緒に乗っていきたくなります。
若葉が美しい季節、今日は八十八夜(立春から88日目)、あと3日で立夏、往く春を惜しむ頃です。生徒の皆さん、有意義な連休後半をお過ごしください。
*1飛行機雲はジェットエンジンからの排気ガスが核になり、水蒸気が凝結して生じるもので、上空の環境によってできる時とできない時があります。どんな時にできるのか調べてみて驚きました。飛行機雲が現れすぐ消えずに長時間残る時は、空気中の水蒸気が多いことを示し、何と、天気が下り坂の前兆なんだそうです。そういうこともつゆ知らず、この歳までポカンと眺めていたとは・・・!?
ちなみに「飛行機雲」は、英語でairplane cloudではなく、contrail [コントレイル]と綴るんだそうです。これは、condensation trailからできた単語でcondensationは「(気体の)凝縮・凝結」、trailは「跡」の意味です。
*2その番組のオープニングナレーションは次のとおりでした。CDまで購入して何度も聴いたので今でも諳んじて言えます。皆さんも声を出して読んでみませんか?これは「声に出して読みたい日本語」だと思います。
遠い地平線が消えて、ふかぶかとした夜の闇に心を休める時、はるか雲海の上を音もなく流れ去る気流は、たゆみない宇宙の営みを告げています。
満天の星をいただく、はてしない光の海をゆたかに流れゆく風に心を開けば、きらめく星座の物語も聞こえてくる、 夜の静寂(しじま)の何と饒舌(じょうぜつ)なことでしょうか。
光と影の境に消えていったはるかな地平線も瞼に浮かんでまいります。
日本航空があなたにお送りする音楽の定期便ジェットストリーム 、皆様の夜間飛行のお供をするパイロットは私、城達也です
【校長】
3乗の展開の公式
いつも本校のHPにお越しいただきありありがとうございます。
今日の2限目、3階の1年生の教室です。建築科や機械科ではモーメントや力の合成など専門の内容が本格的に始まっていました。また、電気科では数学で3乗の展開をやっていました。
3乗の展開とは、(a+b)3=a3+3a2b+3ab2+b3 の公式を使って(2a+3b)3などを求めるものです。
板書されたこの公式が廊下越しに見えて、自分が高校の時の数学の恩師(故人)のことを思い出してとてもノスタルジックな気持ちになりました。
その先生、中学数学で学んだ2乗の展開公式と3乗、(そして発展的に学ぶ)4乗の展開公式の中に出てくる各項の係数を抜き出して板書され「規則性を見つけてごらん」と水を向けられたのです。
どういうことかというと、
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
各項の係数を抜き出すと
121
1331
14641
なかなか見えてこないかもしれませんが、
(a+b)1=a+b
を2乗の展開公式の上段に加えて、係数の並びを少しずらすと
11
121
1331
14641
のように、綺麗な三角形の形に係数が並んでいきます。そして上の段の係数と下の段の係数の間には規則性があります。
この記事をお読みの1年生や中学生の皆さん、もう見抜けましたか?
上の段の左上の数と右上の数の和が下の段にきています!
この三角形は「パスカルの三角形」(Pascal's triangle)と呼ばれています。圧力や応力の単位[Pa]として工業で学ぶ皆さんにとってはおなじみのフランスのパスカル(1623~1662)ですが、彼が最初に気付いたからということでしょうか?名前が残っています。しかし、数学史を紐解くと、実際にはパスカルより何世紀も前の数学者たちも研究していたようです。
従って、14641の下の段の数字の並びは、1 5 10 10 5 1 となりますので、(a+b)5の展開公式は、
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5 となります。
係数の並びは分かるけどa4bとかがどういう仕組みになっているのか、こんがらがっている人がいるかもしれません。
a について見るとa5, a4, a3, a2, a1, a0(a0=1)のように次数が下がり、
b について見るとb0,b1,b2,b3,b4,b5のように次数が上がっています。ここで、aとbの次数を合わせるといつも5次(5乗)になるということは見逃さないで下さい。
まぁ、こういう公式なんて覚えていなくても、気合いで1つずつ展開すれば済む話なんです。でも、覚えていたほうが速く解けるし、計算による脳のエネルギー消費を節約することができるわけです。最後に・・・
Which do you like better, expansion or factorization?
(展開と因数分解、どちらが好きですか?)
私は断然・・・。
【校長】
初志貫徹・有言実行
いつも本校のHPにお越しいただきありありがとうございます。
ここ数日、199名の新入生が入学式の日に提出した「決意作文」を読んでいます。「精一杯」「しっかりと」「挑戦」といった言葉がちりばめられ「やる気」がビンビン伝わってくる作文がある一方、「ご指導よろしくお願い申し上げます」で締めくくられ謙虚さが感じられる作文まで色々あり、とても感銘を受けます。と同時に、私たち教職員もそれに応えるべく頑張らないといけない!という気持ちがいやがうえでも高まります。
この種の作文は就職の際にもよく書かされるもので、その時は意気込むあまり大きなことを書きすぎないのが美徳なのかもしれません。しかし、高校生の決意作文にそれは求めません。作文で綴った本校で頑張りたいという大志(これは今年度の学校テーマです)、その気持ちをいつまでも忘れないでほしいと心から願っているところです。初心忘るべからず*、初志貫徹です!
* 入学式の定番フレーズでもある「初心忘るべからず」、生徒の皆さんもきっと一度は耳にしたことがあるはずです。およそ600年前、能を大成した世阿弥(ぜあみ:多分歴史で習ったはずです)が著わした「花鏡」の中に見える言葉だそうです。
実は、私もこの言葉を引用して、今年度の入学式の式辞を作っていました。でも、長くなりそうでしたのでやめました。今日、改めて調べていたら、世阿弥がいう「初心」とは、「物事を始めたころの新鮮な気持ちや謙虚な気持ち」を指すのではなく「みじめさや未熟さ」を指していると知りました。即ち、「その心を忘れるな」ということは、「あの頃のみじめな状態には戻りたくない」という気持ちを常にもって、芸事に精進しなさいという意味らしいです。そういう隠された意味を知っていると、また違った感じに聞こえます。
では、決意作文で触れられていた本校で「頑張りたいこと」のランキング6位までと、特に印象に残った記述をいくつか紹介します。
頑張りたいこと No1・・・学習 (169名:84.9%)
No2・・・部活 (160名:80.4%)
No3・・・資格取得( 62名:31.1%)
No4・・・生活面 ( 57名:28.6%)【時間を守る等】
No5・・・学校行事( 44名:22.1%)【体育大会等】
No6・・・友達作り( 35名:17.6%)
○ 他人の意見に耳を傾け、相互が納得する意見を見つけ出すこと、そして何かを頼まれた時にその期待に近い結果を残すことに心掛け、人を愛するのはもちろん人から愛される人になりたい。
○ 私には一つの大きな目標があります。それは○○部の仲間と共に全国の舞台で活躍し、日本一になることです。
○ これからこの学校でものづくりを学ぶ中で、誠実の心を大切にしていきたいです。なぜなら、誠実さがなければ良い作品ができないからです。
○ 部活動では運動部のマネージャーになり、選手を支えながら選手と一緒に成長していけるような部活づくりをしたいと考えています。
○ 私の力で○○部を必ず全国大会に出場させます。
○ 僕の好きな諺に、「為せば成る、為さねば成らぬ何事も、成さぬは人の為さぬなりけり」とあります。この言葉の通り、強い意志を持ち、何事にも挑戦し続けていきたいです。
○ 過去の自分を一度捨て、新たに勉学に励み進化した自分を両親に見せたいです。・・・そして、今までお世話になった地域の方々、友達、家族一人一人に恩返しをしたいです。
○ 「努力は人を裏切らない」この言葉を信じ一日一日を大切にしていきたい。
○ 先輩には敬語を正しく使いたい。
○ まだ人吉球磨から甲子園に出場したことがないので、部活での練習に加え、自主トレを人一倍して県代表として甲子園に出場したい。
○ ○○に就職したいという夢を必ず叶えるためにも、高校で取れる資格を全部取るように頑張ります。資格はお金がかかると思うけど、親に感謝して一発で合格できるように頑張ります。
○ 前期試験の面接で言ったとおり、生徒会長になりたいと思っています。
○ 僕が高校で頑張りたいことは全て校訓に当てはまります。剛健誠実、自主自律、好学敬愛の三綱領はとても大事なので、三年間大切に心掛けます。
○ 将来○○関係に進みたい。そこは英語がとても大切なので英語をしっかりとまじめに取り組みたいです。
○ 中学校では給食があってバランスの取れて美味しいご飯を食べてきましたが、もうそんなのはないので、自分でバランスの取れた食事をしていきます。
○ 私が球磨工業高校で頑張りたいことは、つねに「トップ」に立つということです。
○ 最後に僕が挑戦したいことは3年間無遅刻無欠席を達成することです。
有言実行でいきましょう。頑張れ、新入生!
【校長】
spring storm
いつも本校のHPにお越しいただきありがとうございます。
一昨日午後の春の嵐、すごい強風と大雨でしたが、生徒の皆さんはどのように過ごしましたか?
私は窓を叩きつける雨を見ていて、ヘルマン・ヘッセの「春の嵐」を思い出しました。40年前、大学2年の頃に読んだ覚えがあります。確か切ない恋愛ものだったような気がしますが、内容を思い出せません。
あのころ何を考えてその小説を読んだんだろう・・・、そう思うと居ても立ってもいられなくなり近くの本屋さん(ブックオフ)に大雨の中、車を走らせました。あいにく、ありませんでした。
もう1軒行ってみました。またしても空振りでした。諦めて帰る頃は、風雨もだいぶ治まっていました。側溝の蓋には、飛び散った花びらが一杯。桜は2週間前に終わっています。何の花びらでしょう。ハナミズキ?
司書の坂口先生に伺ったところ、「『車輪の下』はあるんだけど・・・」ということでした。残念です。
【校長】
入学式、無事に終わりました。
いつも本校のHPにお越しいただきありがとうございます。
右の写真は、1年生のある教室の黒板に描いてあったメッセージです。「2時間かけて描いた」と担任の先生から伺いました。歓迎する気持ちがすごくこもっています。
改めまして、新入生の皆さん、入学誠におめでとうございます。真新しい制服やスーツに身を包んで臨んだ入学式、いかがでしたか?
実は、入学式が午後3時前に終わり物品販売等があっている中、午後4時45分からは人吉高校敷地内にある凛然寮(人吉球磨地域共同寄宿舎)で入寮式が行われました。私にとっても新入寮生にとっても大変忙しい一日でした。
入寮式も滞りなく終わり自宅に帰り、遅い夕ご飯を食べてホッとしてHPを立ち上げたら、今現在、午後10時32分現在の総アクセス件数は、1005678。
下4桁が5<6<7<8、末広がりでなかなかいい感じの数字です。
数字といえば、今日入学を許可した生徒・学生数は、本科が199名、専攻科が8名の計207名です。
合計の207は、各桁の和が9で3の倍数ですから、3で割り切れます。実際、素因数分解すると32×23となり約数は1,3,9,23,69,207の6個あります。
私としては、200に1不足している199という数字、丁度200じゃないのがとても残念なんですが、199はそれはそれで気になります。
もうお気付きと思いますが、これは素数です。しかも、各桁の数字を入れ替えてできる919,991も素数*ということで「これは一体どういうこと?」と一気にテンションがあがりました。
* 各桁の数字をどのように入れ替えても素数になる数字のことを「完全順列素数」ということを思い出しました。2桁の素数なら11,13,17,37,79の5個で、これを見つけるのは中学数学のレベルです。3桁なら199以外にどのような素数があるのか・・・?
けっこう面倒でしたが、199以外に113と337を見つけることができました。4桁ではどうなるのでしょうか・・・? 気が遠くなります。
ところで、199という素数は、各桁を循環させると991,919となり、そのいずれも素数ですので、「循環素数」でもあります。実は、199よりも2少ない197も197→971→719と各桁を循環させると、いずれも素数になりますので循環素数ですが、これは完全順列素数ではありません。(197,179,719,971は素数ですが、791が7×113、917が7×131と素因数分解されます)
最初に話題にした総アクセス件数の1005678の5,6,7,8の並びにヒントを得てごちゃごちゃやっていたら、またしても面白い性質をみつけました。何と199は、連続する6つの整数の平方の和で表されるということです。
数式で書くと 199=32+42+52+62+72+82
「美しい!」と見とれて、寝るのも忘れてしまいそうです。こうなると、専攻科の入学生の数である8にも何か意味を見出したくなります。
色々考えてみましたが、特に思いつきません。苦し紛れですが、199と8を結び付けるものとして「8n-1」ということ位でしょうか?
199=8×25-1
(あれ!、1不足が出てきました。199は、8n-1型で表される12番目の素数になります)
話は大きく変わりますが、桜が終わりハナミズキが青空に美しく映える頃となりました。右の写真は校長官舎の庭にあるものです。
歌手一青窈(ひとと よう)さんの歌でも有名なハナミズキ、図書館の植物図鑑によると、日本における植栽は、1912年に当時の東京市長だった尾崎行雄がアメリカ合衆国ワシントンD.C.へ桜(ソメイヨシノ)を贈った返礼として1915年に贈られたのが始まりとありました。日本人が桜を愛するように、アメリカではハナミズキが最も愛されるのだそうです。
明日は対面式、明後日は交歓会と、新入生を対象とした行事が続きます。
【校長】
球磨工の情報を発信中!
リンクはこちらから
学校情報
〒868‐8515
熊本県人吉市城本町800番地
TEL 0966-22-4189
FAX 0966-22-5049
E-mail
kuma-th@pref.kumamoto.lg.jp
熊本県教育情報システム
登録機関
管理責任者 校長 坂本道彦
運用担当者 ホームページ係