徒然雑記帖
平成30年度の就職試験を振り返る
就職試験ではどのような問題が出題され、面接で何が問われたのでしょうか。概要を知っておくことは学校を預かる責任者として大事なことであると思い、3年生の皆さん方が提出した受検報告書に毎年目を通しています。
集団討論で「日本食と言えば寿司か蕎麦か」というお題で議論させた企業がありました。一体どんなことが話し合われたのだろうと興味津々です。
また、計3社で「中学校で必須教科を1つだけ加えるなら何か」と面接で問い、「学校の教科で1つ増やすとすれば何か。理由も添えて述べなさい」と作文で出題していました。昨年度は、「祝日に1日付け加えるとしたら何?」とあり、「エッ?!」と思ったところでしたが、今年は「教科」です。一体どのような答を期待しているのでしょうか。もし学生時代に学び足りなかったことを聞いているのだとしたら、私なら「年金制度」と答えるかもしれません。
ということで、いくつかの問題を紹介します。(【 】内に地区と業種を示しました。3社以上で出題があった問題は【多数】と表記しています)
1、2年生の皆さん方は、このような問題に来年、再来年に直面します。今の実力でどのくらい対応できますか?
作文
・「入社3年後の目標」(「20年後の自分について」「社会人になってチャレンジしたいこと」「目標を達成するために継続して努力したこと」「社会人になるに当たっての心構え」「大工になってやってみたいこと」等も)【多数】
・「高校生活で一番困難だったこと」(「それをどう乗り越えたか」「その結果何を得たか」「それを今後どう活かすか」「今まで一番打ち込んだこと」「私が一番自信をもっていること」等も)【多数】
・「働くということはどういうことか」(「私にとって働きやすい職場とは」「仕事を通してどういう力をつけたいか」「働きながら成長するために心がけたいこと」「仕事をする上で大切なこと」等も)【多数】
・「製造業で一番必要なコンプラインアンス意識とは」【中京・製造】
・「学校の教科で1つ増やすとすれば何か。理由も添えて書きなさい」【中京・製造、中京・鉄鋼】
・「あなたを漢字1文字で表現するとしたら何か。理由も書きなさい」【中京・鉄鋼】
・「次の2つの中からあなたが修理できるものを選び、今まで学んだことを活かして修理の手順や必要な道具を詳しく書きなさい」【関東・保全】
①エアコンの効きが悪い ②パソコンでインターネットに繋がらない
・「お年寄りと関わる中で感銘を受けたこと」【熊本・介護】
集団討論
・「皆さん達4人はチームです。4人で会社を起業するとしてあなた達は何を売りますか」【中京・製造】
・「ドラえもんの四次元ポケットがあったとして、のび太君と世界を幸せにする道具をそれぞれ一つだけ選び、その理由並びにその道具の欠点を話し合ってまとめなさい」【中京・鉄鋼】
・「中学校で必須教科を一つだけ加えるとしたら何か」【中京・製造】
・「中高生のインターネットの依存の対策は」【九州・製造】
・「成功体験と失敗体験のどちらが人を成長させるか」【九州・電力】
・「KYT(危険予知訓練)活動。絵を見て危険なところを探し、安全策を5人で討論しなさい」【近畿・製造、中京・製造】
・「東京オリンピックを盛り上げるためには」【中京・製造】
・「社会のルールを守らない人はなぜ守らないのか、その解決策は」【九州・製造】
・「日本食と言えば寿司か蕎麦か」【関東・鉄道】
・「飛行機が故障して砂漠地帯に不時着した。そんな中あなた達5人は12個のアイテムを手にして逃げることになりました。12個の必要なアイテムを挙げて順位を決めなさい」【中京・製造】
・「学生と社会人の違い」【中京・製造】
・「ある企業には野球部があり、ファンクラブもある。同じように部を作るとしたら何部を作るか。チーム名、スローガン、集客方法、資金をどうするか」【関東・鉄鋼】
筆記試験(時事問題系の一般常識)
・「熊本県知事の名前をフルネームで漢字で書け」(「今の内閣総理大臣の名前」、「校長の名前」等も)【多数】
・「熊本城を建てた人は」【熊本・設備】
・「オリンピックの種目で新種目4つのうち1つ答えよ」【関東・電力】
・「自民党の総裁選挙に出馬するのは安部普三首相とあと一人は誰か」【関東・保全】
・「2018年、テニス全米オープンで優勝した選手は」【九州・建設】
・「東京オリンピック、パラリンピックのキャラクターは」【関東・製紙】
面接
・「高校時代に頑張ったこと」【多数】
・「年上の方や上司と仕事をしていくわけだが、どうすると上手く付き合っていけるか」【多数】
・「働くとはあなたにとってどういうことか」(「仕事とは何か」等も)【多数】
・「ジュニア・マイスターとは何か」【多数】
・「あなたが知っている重機の名前は」(「弊社の製品の名前は」等も)【多数】
・「弊社を漢字1文字で表すとしたら何か」(「漢字2文字なら何か」、「あなた自身を漢字1文字で表すと何か」等も)【多数】
・「あなたにとってどのようなことがストレスか。ストレス発散法は何か」【多数】
・「自分を動物に例えるなら」(「自分を車の部品に例えると何か。またその理由は何か」等も)【多数】
・「不得意な科目をどのように努力し克服したか」【中京・製造】
・「昨夜は寮に泊まってもらったが、同室4人とコミュニケーションを取ったか」【近畿・電力】
・「人の意見を聞いて動くタイプか、それとも自分で決めて行動するタイプか」【熊本・製造】
・「初任給をどう使うか」【中京・製造】
・「SNSに関してどのようなことに気をつけているか」【関東・鉄鋼】
・「あなたにとって苦手な人はどんな人か。その対処法は何か」【関東・建築】
・「あなたが住んでいる町の特徴は」【中京・建築】
・「ふりこ、ストップウォッチ、棒の3つを使って振り子の周期を確実に測定する方法は」【熊本・製造】
集団工作等
・紙20枚とはさみ、テープを使って8人で共同して高いタワーを作る。ただし、紙と紙との接合にテープを使ってはいけない。タワーの名称、工夫した点を話し合い、代表一人が発表。【中京・製造】
・ミニゴルフで得点を競う。(各班7人。まず、司会1、書記1、タイム1、応援2を選ぶ。選手と各係は重複可。各グループで「動作手順」を作成し、その手順通りに選手1人が3球ずつ打って3人の選手の合計点を班ごとに競う。その後、上手くできた点、できなかった点を面接で聞かれる)【中京・鉄鋼】
・マシュマロタワーにチャレンジ!【関東・電力】
パスタの乾麺20本、テープ90cm、たこひも90cm、マシュマロ1個(頂上につける)これらを使ってより高いタワーを4人で作りあげる。(説明5分、個人ワーク5分、作戦タイム13分、制作20分、反省10分)
まとめ
作文のお題は、毎年定番のものばかりです。面接では、社会の出来事を反映した時事問題を問う企業があるようです。グループワークや集団討論を課す企業が年々増え、採用に当たりコミュニケーション能力重視の姿勢は一貫したものを感じます。また、昨年度と同じ出題が続いている傾向が非常に顕著で、過去問をしっかり解いておく必要性を痛感します。
最後に・・・、生徒諸君が残していた感想には、「工場内は5Sが徹底していて、ゴミ、油など全く落ちていなかった」、「工場内は隅々まで掃除が行き届いており、さすがだと思った」などが沢山あり、普段から5Sを口うるさく指導している成果が出ているな・・・と嬉しく思ったところでもあります。
【校長】
追伸
・6□4□7□5=29 【多数】
□に+,-,÷,×を入れて式を完成させる問題を短時間にできるだけ沢山解くもので、SPIの常連で筆記試験でも多くの企業が出題しています。ちなみにこの答は順に+、×、-
このような算数系の問題(小町算)は、普段から私のサイトを見て数に関する感覚を磨いておくと得意になるかもしれません。
この問題を見て閃きました。今日12月19日は、今年最後の素数日*です。それを記念して日にちの数字をそのまま並べた1219をこの式で作ることができないかということです。即ち
6□4□7□5=1219
暫く考えたところ、何と全部「+」だけでできあがりました。
6!+(4!!)!!+7!!+5!!!=1219
「階乗、しかも多重階乗なんか使ってずるい」と言われそうですが、「+だけでというのが凄い偶然だ」と思わず唸ってしまいました。何かいいことがありそうです。
*素数日とは
平成30年12月19日を301219のように6桁で表すと素数になる日です。このことについては、今年1月1日の記事で一度紹介したところですが、改めて書き出すと以下の通り24日あり、今日は今年の最後の素数日になります。
300109、300119、300221、300301、300317、300319
300323、300331、300413、300427、300511、300623
300719、300721、300809、300821、300823、300929
301013、301027、301123、301127、301211、301219
西南戦争と人吉、そして村山台地
俳優の鈴木亮平さんが主演を務めるNHKの大河ドラマ「西郷どん」が昨夜とうとう終わってしまいました。最後2回は「西南戦争」での激しい戦闘の様子が圧巻でした。
言うまでもなく、西南戦争(西南の役)は、1877年(明治10年)に九州で、明治新政府に対して反感を持っていた鹿児島の士族達が西郷隆盛を盟主にして起こした武力反乱です。明治初期に起こった一連の士族反乱の中でも最大規模のもので、我が国最後で最大の内戦と言われています。
平和的な交渉を望んだのに賊軍となってしまった西郷軍、「最後の侍」として日本のために使命を全うし、こうやって歴史になっていってしまったのかと感無量の思いで見ました。
ところで、生徒の皆さんは、ここ人吉市が西南戦争の激戦地の一つだったということは大丈夫ですか。「西郷どん」では先週(第46話)、解説字幕で「人吉」という地名がほんの一瞬出ただけでしたが・・・。
そして、この戦争が献血等の際にお世話になっている日本赤十字社*発足のきっかけになったということは知っていましたか?(「西郷どん」ではこのことは扱われなかったようですが・・・。)
本校の校歌の1番は、「ふるさとの文化の朝に 風さやか村山台地♪」の出だしで始まります。本校が所在するこの村山台地こそ、西南戦争を語るうえではずせないキーワードになります。
その説明書きや史料によると、薩摩軍は、九州を北上し、熊本城を攻めますが、中々うまくいかなかったようです。1873(明治6)年3月、田原坂の戦いで敗れた薩摩軍は熊本城をあきらめ、追ってくるであろう官軍を迎え撃つために人吉にしばらくの間滞在しました。西郷隆盛は永国寺に本部(宿舎)を置いて戦争の指揮を執ることにし、球磨川南岸に兵を集結しました。
一方、薩摩藩を追って人吉に入った新政府軍は、人吉城下を一望でき見晴らしの良い村山台地に砲台を築きました。6月1日、眼下球磨川に展開する薩摩軍への総攻撃を開始。球磨川を挟んで砲火が飛び交いました。薩摩軍には人吉の士族たちも多数合流していましたので、父子、兄弟、甥と叔父が敵味方に分かれて戦ったとありました。(こういう記述は、中世の保元の乱(1156年)を彷彿させます)
薩摩軍の砲弾は、政府軍の本営まで届かず、球磨川を挟んでの攻防は官軍の圧勝で終わり、薩摩軍は、町に火を放って人吉から退却。町は、戦闘と放火により、灰燼に帰しました。それだけでなく、この人吉根拠地の期間中、薩摩軍はこの地域に苛烈な軍政を布き、政府軍と内通した容疑をかけられた住民が捕縛され、証拠も詮議も不十分なまま私刑同然に処刑する残虐が加えられているそうです。薩摩軍は総崩れとなって敗走、人吉を捨てて田代、大畑方面へ退却し、大畑に陣を敷きます。・・・以下省略します。
昨年は西南戦争後140年目に当たるということで、当時を振り返る催しが各地で行われたり、関連本も沢山出版されました。興味がある人は調べてみると、自分が住む人吉について新たな発見があるかもしれません。
また、いつの世も高台というのは戦局を有利に進めることが多いわけですが、本校はそんな悲しい歴史が残る村山台地に所在していることを知っておくことは大事なことかもしれません。
【校長】
*昨年の夏休み期間中に生徒会の生徒たちが、「青少年赤十字リーダーシップ・トレーニング」という活動に参加してきました。生徒たちがもらってきたガイドブックの中に赤十字の歴史について次のように触れてあります。以下、長くなりますが抜粋しておきます。(参考までに)
日本赤十字社もスイスで最初の赤十字が誕生した時と同じように、戦いがきっかけで誕生することになりました。戦いに大きな力をもっていた鹿児島の士族である反乱軍は熊本まで攻め上がり、熊本城や田原坂を中心に明治政府と反乱軍で激しい戦いが繰り広げられ多くの負傷兵が出ました。負傷した兵士の多くは戦場に倒れたままで、充分な看護も受けられず苦痛に耐えかね、お互い刺殺しあった者もいたと言われています。
九州での悲惨な戦いを東京の地で聞いて悲しく頭を痛めていた元老院(今の国会)議官の佐野常民は、負傷した兵士がなんの救護も受けず放っておかれていることが残念でなりませんでした。
佐野常民はこれまでにヨーロッパを旅行したことがあり、その時にヨーロッパには戦場の負傷兵を敵・味方の区別無く救護する赤十字という団体があることを知っており、日本でもそのような団体を作る必要があると考えていました。この西南戦争の時に、赤十字のような団体があれば、負傷兵の生命を救うことができると考えたのです。
そのことを友人の元老院議官の大給恒(おおきゅうゆずる)に相談したところ、大給恒も大いに賛成してくれ、2人は具体的な計画をまとめました。救護団体を作りそれを博愛社と名付け、明治政府に救護活動をするための願書(ねがいしょ)を提出しました。
しかし、願書に記されていた敵・味方の区別無く救護するという考えは当時の人々になかなか受け入れられず、明治政府は、政府に逆らう反乱軍の兵士まで救護するという趣旨のこの願書を認めませんでした。
佐野常民はあきらめませんでした。認められなかった願書を持って戦場の熊本へ向かい、熊本城で政府軍の総指揮者として反乱軍の鎮圧にあたっていた有栖川宮熾仁親王(ありすがわのみやたるひとしんのう)のもとへ、直接博愛社の設立の許可を願い出たのです。有栖川宮熾仁親王はこの願いを聞き入れ、その場で博愛社の設立を許可しました。
1877年5月1日のことです。日本赤十字社の創立記念日はこの日を記念して5月1日としました。これにより「博愛社」の救護員は直ちに現地に急行し、両軍の負傷者の救護にあたりました。この活動は、当時、敵の負傷者まで助けるという考えが理解できなかった人たちを驚かせました。
西南戦争から9年たった1886年(明治19年)、明治政府はジョネーブ条約へ加入しました。そして、博愛社は翌年の1887年(明治20年)に名前を日本赤十字社と改めることになり、ここに日本赤十字社として国際赤十字の一員に加わることになりました。
さらに1919年には、赤十字の平時活動を推進する国際赤十字・赤新月社連盟の創設に参画しました。
今日では、戦時平時の別なく幅広く赤十字の活動の推進に努めています。
長距離走大会と心拍数
いつも本校のHPにお越しいただきありがとうございます。

途中で3人がリタイアしましたが、その他の生徒たちは全員が規定時間内(2時間)に走り抜くことができました。
力強い走りでみんなを先導した男子1位の鶴田舞杜君【3MA】(43分3秒:302.0m/分)、女子1位の千代村春花さん【1A】(48分6秒:228.7m/分)をはじめ、上位15人の皆さん方を表彰しました。そして、団体の部では2MBが優勝しました。誠におめでとうございます。
沿道周辺の皆様には、今年も大変御迷惑をおかけしましたが、終始温かいご声援をいただきありがとうございました。また、保護者の皆様には豚汁を振る舞っていただき大変ありがとうございました。

1113、この数、どこかで耳にした数だな・・・と思って記憶の糸を手繰ったら・・・何と昨日、買い物をして支払ったお金でした。
1113円
ある意味、凄い偶然です。
1113は1113=3×7×53と素因数分解されるので、素数ではありませんが(約数は、1, 3, 7, 21, 53, 159, 371, 1113の8個)、今日12月13日の数字をそのまま並べた1213、こちらは素数です。
偶然といえば、凄いことが今朝起こりました。3日前(12月10日)の記事で1248421という数がアクセスカウンター以外で実際に現れるとしたらどんな場面なのかと話題にしました。
何と、それに近い数字が今朝現れたのです!
私、毎朝、手首式血圧計で血圧を測っています。最高血圧●●●mmHg、最低血圧▲▲mmHg、脈拍数★★拍/分 をそのまま並べると、●●●▲▲★★という7桁の数になります。今現在、学校のHPの総アクセス数が7桁を刻んでいますので、血圧計が表示した7桁の数とHPの総アクセス数が極々小さな確率ですが同じになる可能性があります。そういう日がいつどんな状況で現れるのか、毎日楽しみに血圧を測って、表示された数字を眺めています。

気になって心拍数が20前後の動物を検索したところ、ありました。象です。象で思い出すことがあります。生徒の皆さんは「哺乳類の心拍数と寿命は反比例し、一生の総心拍数は約20億拍で一定」という学説を聞いたことがありますか?有名ですから、耳にしたことがある人は多いかもしれません。
それによると、象(20拍/分)の寿命は、20億÷(20×60×24×365)を計算しておよそ70年、ちなみに人(70拍/分)は、20億÷(70×60×24×365)で、およそ54歳になります。(現在、人の平均寿命は男女とも80歳を越えていますが、医療と食生活の進歩によるものと考えられているようです)
とにかく、体が大きい(体重が重い)動物ほど1分間の心拍数が少なく長生きで、体が小さい(体重が軽い)動物ほど心拍数が多く寿命が短いという「心拍数と寿命の間の反比例の法則」そして、「哺乳類の心臓は総心拍数が20億回で打ち止め仕様」、どちらも味わい深い説です。
心拍数が少ないほど長生きできるというのなら、中・高校生の時にしっかり運動をして心肺機能を高めておき、平常時には70拍/分よりも低い、例えば60、50拍/分といった心拍数で動く強靱な心臓を作っておけば長生きできるということでしょうか?それとも、運動をやっていると、その分当然心拍数の増加を伴うので、やっただけ寿命が短くなるということでしょうか?
若い時に作った身体で残りの人生を生きていくというのは確かですが、こういうことが運動生理学などに無知の私にはよく分かりません。
ちなみに本日の長距離走大会でこんな計算をしてみました。もし、最大心拍数200拍/分で1時間半ずっと走っていたとすると、その間に心臓は1,8000回(200×90)打っていたことになります。これは生涯の総心拍数20億回に対してどのくらいの割合になるかというと、0.000009即ち9ppm*になります。この数字、一体どう捉えればいいのでしょう?
今日の長距離走大会、どのくらいまで心拍数が上がったか脈を取った人はいますか?身長や体重だけでなく、心拍数や血圧といった内臓機能についても、自分の身体のスペックとして時には気にしてみましょう。
【校長】
ppm*(パーツ・パー・ミリオン)について
ppmは、「parts per million」の頭文字をとったもので、100万分の1の意味。主に二酸化窒素などの大気汚染物質をはじめとする公害分野や、食品添加物などの濃度、岩石中の微量元素の組成、半導体中の不純物量を示す目的などでよく用いられるが、不良品発生率などの確率を表すこともある。
拵える、誂える、設える

見事な西高東低の気圧配置となり寒い週末でしたが、生徒の皆さんはどのようにお過ごしでしたか?
私は京都の同志社大学に行っていました。京都検定を受験しにです。
2,3年生の皆さんは、昨年2学期の終業式で次のような話をしたことを覚えているかもしれません。
「私、せっかく人吉の地に赴任したから、地元をよく知るためにも『人吉球磨検定』を受けようと決心した。・・・テキストを買って勉強してきたが、願書請求の段階になって実施してないことを知った。・・・受験生が集まらず3年前から休止になっているらしい。・・・ここ人吉は京都と雰囲気が似ていることから『小京都』と呼ばれているが、雪辱を果たすためにも本物の京都検定を受けたい。・・・」と。
一時期ブームになっていたご当地検定、その嵐も過ぎ去り東京の「大江戸検定」、奈良の「奈良まほろばソムリエ検定」、京都の「京都観光文化検定」(これが正式名称)の3つがいまだに沢山の受験生を集めており、その中でも絶大な人気があるのが通称「京都検定」のようです。
私、検定試験を受けるのはおよそ10年前の技能検定以来久々です。この京都検定、今の学校教育で育むことが重要視されている思考力・判断力・表現力等とは(論文が課せられる1級は別として少なくとも2級・3級では)無縁の世界です。ひたすら暗記力だけの勝負で、そういう意味では潔い試験と言ってもいいかもしれません。京都に行ったことは高校の修学旅行を含めわずか3回しかありません。地図を広げ碁盤目状の道路配置を頭に叩き込んだうえで、数多ある寺社を始め色々なことを全て一から覚えていきました。
とは言っても、この歳になると記憶は忘却との闘いです。今日10覚えても次の日には9忘れているといった状態が続き、途中何度か断念しようと弱気になりました。くじけそうになるモチベーションを奮い立たせてくれたのが、主催者が公表しているデータです。それによると、1級~3級のどの級も受験生が一番多い層が50歳~60歳(H28年度)ということで、記憶力の減退に苦しんでいる同志がきっと沢山いるはず?・・・、そのことだけが心の支えでした。
そういうことで、試験勉強では公式テキストに加えて市立図書館や県立図書館にある京都本を読み漁(あさ)りました。特にものづくり関係の本を中心に。そして気付いたことがあります。今日のタイトルにある「拵える、誂える、設える」という動詞です。順に「こしらえる、あつらえる、しつらえる」と読むようです。
京都のものづくり(伝統工芸)については、公式テキストブックの中に次の一節があります。
京都の伝統工芸の「匠の技」は朝廷、巨大社寺、貴族らがスポンサーとなり一流の審美眼で京の伝統工芸にさらなる技芸の精進を促し、これに応える十分な職人芸が発達した。・・・(途中略)・・・宗教都市であり、文化都市でもある京都は、現代でも工芸美術品の需要があり、それが重層的に影響しあいながら類いまれな「手の匠」を生み出しており、国の伝産法(伝統的工芸品産業の振興に関する法律)に基づいて、経済産業大臣が指定する伝統的工芸品に京都府内の17品目が指定を受けている。・・・
これら3つの大和言葉風の響きをもつ動詞、京のものづくりを語る本の中になぜか高い頻度で出てきます。私自身はこれまで稀に耳にしたことはありますが、いずれも自分が普段使う語彙ではありません。それだけにすごく目についたのかもしれません。意味も曖昧でしたから、念のために辞書で調べてみました。
●「拵(こしら)える」とは、ある材料を用いて、形の整ったものやある機能をもったものを作り上げること。
●「誂(あつら)える」とは、自分の思いどおりに作らせる。注文して作らせること。
●「設(しつら)える」とは、ある目的のための設備をある場所に設けること。
語義を読んでも、日常使わない言葉だけに分かったような、分からないような変な気分です。「誂える」は、お金を払って自分ではない他の人(専門家)に頼むニュアンスが強いから、ものづくり系の動詞にも拘わらず「手偏」ではなく「言偏」なのかなぁ・・・?とか思いつつ、このような小難しい動詞が似合う京の一流の職人たちによるものづくりの奥深さに思いを巡らしたところです。
こうした言葉で語られる伝統工芸に限らず、寺社や史跡・名勝から建築、庭園、美術、芸能に至るまで広く(浅く)触れたことで、日本の政治文化の中心であった京都の奥深い魅力を新たに発見しました。その意味で京都検定、私にとってはとても有益でした。また、知識が増えていく楽しみが記憶力低下の厳しい現実を突きつけられる辛さを凌駕してワクワクしたことも実感です。

この数、右から読んでも左から読んでも同じになる回文数です。それに加え、上4桁の1248は初項1、公比2の等比数列をなし、下4桁の8421は初項8、公比(1/2)の等比数列になっているという点でも面白い数です。ちなみに素因数分解すると、素数2つの積になる「半素数」でした。
1248421=29×43049
ですから、その約数は1,29, 43049, 1248421の4個になります。
ちなみに1248421という数がアクセスカウンター以外で実際に現れるとしたらどんな場面でしょう?私、超々気になって検索をかけてみました。
ありました。今、お茶の間の話題をさらっている某自動車メーカーがpdfで公表している売り上げ報告書の中に、次の表記を見つけました。こういう偶然ってあるんですね!
・・・販売台数は、前年比9.4%増の1,248,421台となりました。・・・
最後に、今日取り上げた1248421について、数字の並びをそのままにして、加減乗除等の記号を入れて、この数字が現れた日にちであり、開戦記念日でもある12月8日をそのまま並べた128を拵えてみます。
-1+24+84+21=128
1+2+4×8×4-2-1=128
(124+8-4)×(2-1)=128
1×2×4×8×4÷2×1=128
124+(8÷4+2)×1=128
1+248÷√4+2+1=128
{12√4-(8+4×2)}×1=128
1×2×√4×8!!!!×(4-2-1)=128
12×4!!+8!!!!+√4-2×1=128
{12÷4×8!!!!+(4!!)!!!!}×(2-1)=128
{12!!!!!!+48+4×2}÷1=128
12!!!!!!+sin-1(4/8)+(4!+2)×1=128
cos-1(1/2)+(4!!)!!!-8÷√4×(2+1)=128
tan-1{√(1+2)}+4+8!!!-4!!×2×1=128
ということで、広島~新神戸間の1時間ちょっと間に14通り立式しましたが、まだまだできそうな気がします。皆さんだったらどのような式を拵えますか?誰も考えつかないという渾身の一式ができあがったら是非教えてください。
ちなみに私もサイン・コサイン・タンジェントの全てが入った奇抜な式を立式しようとだいぶ試みましたが・・・
sin-1(1/2)+cos-1(4/8)-4-2+tan-1(1)=129 ×

受験に向かっているのに、小町算なんかで遊んでないで「追い込みの勉強したら・・・?」とか言われそうです。
でも、困ったことにポテチと一緒で「やめられない・止まらない」なんですよね、これが(..;)
【校長】
12月3日→123で思い出すこと
いつも本校のHPにお越しいただきありがとうございます。月が変わってとうとう師走に突入しました。1日(土)は小春日和でしたが、昨日2日(日)は昼から雨が降り出し少々肌寒い天気になりました。期末考査も終わりましたが、生徒の皆さんはいかがお過ごしでしたか?
私は昨日、多良木町で行われていたサイテク祭り( Science & Technology の略らしい)で、本校溶接部と電気工作部がブースを出していたこともあり、様子を見に行きました。天気がぐずついていたせいか、昨年度よりも若干客足が鈍ったということですが(主催者発表)、本校のロボットやUFOキャッチャーの前には写真のように終日賑わっていました。
事業所の皆様には大変お世話になりますが、御指導を宜しくお願いします。
ところで、数日間出張が続いていたので、たまっていた仕事をしようと、今日はいつもより2時間余り早く学校に来ました。到着後すぐHPを開いた時(午前5時45分)の総アクセス数は1242013。
これはどのような数かな?素数ぽいけど・・・と、いつものように素因数分解をしてみました。電卓を暫く叩きましたが、なかなかできません。根負けしてネット上の素数判定機にかけたわけですが、驚くべき事実に気付きました。
まず、1242013 は、先日から話題にしている「半素数」(2つの素数の積として表される数)でした。
1242013=41×30293
従って、その約数は 1, 41, 30293, 1242013の4個です。
何に驚いたのかというと、今日の日にち12月3日の数字をそのまま並べた123*も 123=3×41 と素因数分解される「半素数」であり、しかも41が共通していたということです。
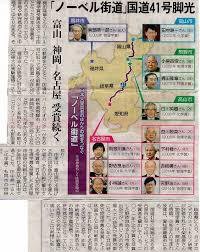
それはさておき、この41という数、なぜか神秘的です。皆さんは、名古屋市と富山市を結び、日本列島をほぼ真っ二つに縦断する国道41号線のことを耳にしたことがありますか?
全長約250キロのこの道沿いから、ノーベル賞受賞者が相次いでいるということで、この国道41号線は別名「ノーベル街道」と呼ばれているそうです。日本でノーベル賞を受賞した方の生家の何と3分の2が41号線脇にあったそうです。右はネット上で見つけたそのことを報じる新聞記事です。偶然にしてはとても神秘的ですよね。
かつては出世魚のブリをはじめとする生活物資が運ばれていたらしいですが、この業績にあやかって「現代のお遍路」をする人たちもいるそうです。
最後に、今日取り上げた1242013について、数字の並びをそのままにして、加減乗除等の記号を入れて、今日話題にした41と123の2つの数を作ることに挑戦してみます。
1+2+42+0-1-3=41
124+2+0!-1-3=123
あまりにも簡単にできて、何だかな~です。もう一組作ってみます。
12×4-2-0!-1-3=41
-1+2+√4+20×1×3!=123
う~ん、ピンときません。もう一組作ってみます。
-1-2×4+2+{(0!+1)×3}!!=41
(1+2)4+{(2+0!)!+1}×3!=123
何通りもできそうですが、皆さんだったらどんな式を作りますか?
*123で思い出すこと
123と聞いて真っ先に思い浮かぶものといえば、33年前、昭和60年(1985年)8月12日に起きた日本航空123便御巣鷹山(おすたかやま)墜落事故です。単独事故としては史上最多の死者を出した航空機事故(乗員15人を含む520人が死亡)でした。
当時、私は教師として駆けだしの頃で、数学の免許を取るために東京の玉川大学の夏期講習会(スクーリング)に2週間通っており、明日帰熊という日でした。
あの日あの時(午後7時頃)、突然テレビの画面が「飛行機が消息不明」と報じるニュースに切り替わった瞬間は衝撃的で、鮮明に覚えています。その後は夜更けまでテレビにくぎ付けとなり、仮眠してはまたテレビを見るといった感じで、生涯忘れえぬ事故になりました。
時を経て、あの大惨事を直接知らない若い人たちが増えてきています。次第に風化が進むのは致し方ないのかもしれません。
そんなことを時々考えていたつい先日、これまた衝撃のニュースが報じられました。何と、イギリスのヒースロー空港で、乗務直前の日本航空のパイロット(副操縦士)から、基準値の9倍を超えるアルコールが検出され酩酊状態だったというものです。2日前の新聞では、現地の裁判所は「乗客乗員を危険にさらし、大惨事を引き起こすおそれがあったとして、被告に禁錮10カ月を言い渡した」と。
副操縦士は42歳とありました。今から33年前といえば9歳になりますから、この事故を直接知らない世代なのかもしれません。しかし、大惨事を引き起こした当該会社の社員ですし、社内教育で「御巣鷹を忘れるな!」と何度も聞き、徹底した安全教育を受けていたはずです。「それにも関わらずなぜ・・・?」という思いが、私たち大人の飲酒運転が無くならないこととダブってしまいます。
パイロットは離着陸の時だけでなく、常に緊張状態を要求される特殊な職業であり、お酒にストレス発散を求める向きがひょっとしたらあるのかもしれません。でも、飛行機の事故はとにかく、とにかく悲惨です。「飛行機をコントロールする前に、自分をコントロールできる人」が操縦する飛行機じゃないと誰しも乗りたくないはずです。
高校生を含めた若い人たちのアルコールの問題に敏感になっている時と偶然に重なったこともあって、今年一番ショックを受けたニュースの一つでした。
【校長】
√1234321=?
いつも本校のHPにお越しいただきありがとうございます。生徒の皆さん、3連休、いずれも天気に恵まれましたがいかがお過ごしでしたか?今日から期末考査が始まりました。全力を尽くしてください。
ところで、本校のHP、最近1日におよそ1100件(1時間当たり45件)のアクセスがあっています。

この数字、ちょっと面白いと思いませんか? 右から読んでも左から読んでも同じ数という意味で。
このような数字を「回文数字」といい、趣味の数学の分野でしばしば研究の対象になっています。このことについては、偶然にも丁度1年前、昨年の11月27日の記事で紹介済みです。(詳しくはこちら → 総アクセス数 842248 → この数字の魅力)

最上桁から数字が昇順に並び、何ともいい数字です。
ということで、今日はこれら2つの数字について考察してみます。
まずは今日のタイトルである √1234321=?
これは数年前の3年生の受験報告書の中にあった、即ち就職試験に出題された問題でもあります。学校では習わないはずの開平法(ルートの近似値を筆算で計算する素朴な方法)の技量を問う問題とは思えません。以下に述べる知識の有無が問われているはずです。
111や11111のように1がいくつも並んだ数字を「レピュニット」(repunit【repeated unitの略】)ということについても、今年の7月17日の記事で紹介済みです。(詳しくはこちら → 総アクセス数1111111と7月17日と239)
その日の記事で、レピュニットに関する頭の体操を3問出題していました。それとも関連する問題になります。
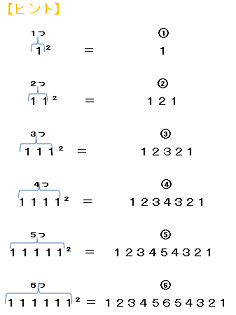
そこから何か閃きません?
・・・・
・・・・ thinking time ・・・・
・・・・
分からない人は左の【ヒント】を見て考えてください。
もう大丈夫ですよね。
4段目の④をみながら、答は1111
では、数としての1234321を考察してみます。まず素因数分解です。
1234321=112×1012
従って、その約数は、1, 11, 101, 121, 1111, 10201, 12221, 112211, 1234321の9個。何と約数まで全て回文数になっているのがある意味不気味です。
次に1234567 果たして、これは素数でしょうか?
色々な素数で割ってみました。なかなか素因数が見つかりません。根負けしてネット上の素数判定機にかけてみたら、素数ではありませんでした。
1234567=127×9721
ということで、その約数は 1, 127, 9721, 1234567の4個になります。
従って、もし「x2+9848x+1234567 を因数分解しなさい」という問題があれば、その答は (x+127)(x+9721)となります。中学程度の因数分解ですが、難しいですよね(..;)
でも、こういう因数分解が某私立高校の数学の入試の1番の集合問題の中に出題されていたのを見たことがあります。勿論、最後の定数項は1234567みたいな7桁の数字ではなく4桁の数字でした。その数字、随分昔のことで正確に覚えていませんが、例えば「x2-670x-2019を因数分解しなさい」ならできますか?
2019は来年の西暦です。閃き力を問う問題かもしれません。
答は(x+3)(x-673)です。定数項はわずか4桁ですけれども、当時、因数分解の専門書の中で「高校受験史上最難の因数分解」とか騒がれました。実際、限られた時間で3と673の組み合わせを見つけるのは至難の技かもしれません。
知っている人もいるかもしれませんが、1234567のように2つの素数の積として表される自然数のことを「半素数*(semiprime:【セミプライム】)」と言います。素数は無数に存在するため、半素数も無数に存在することになります。ちなみに最小の半素数は4(2×2)ですし、先ほど取り上げた来年の西暦である2019も(3×673)で半素数です。
最後に、今日取り上げた1234321と1234567の2つの数について、数字の並びをそのままにして、加減乗除等の記号を入れて、今日の日にち11月27日の数字をそのまま並べた1127を作ることに挑戦してみます。
12!!!-(3!)!-(4!!)!!!-(3!)!!!+2-1=1127 → 11月27日
1234-5!+6+7=1127 → 11月27日
*「半素数」について
名前がついているぐらいだから、数学、特に暗号化理論の分野では研究の対象になっています。ここでは極々簡単に。
インターネットでやり取りするデータは、常に悪質な第3者に傍受されているという前提で利用しなければなりません。クレジットカードの番号を入力するとき、その番号が盗まれて第三者に不正に使われないかとか心配したことがある人も多いはずです。
そこで、たとえ盗まれても絶対に読まれないように、データを暗号化する必要があります。その時にデータに素数を使った「鍵」を掛けます。2個の素数の積を求めることは簡単ですが、半素数を素因数分解して元の2個の素数を求めることは、その桁が大きくなればなるほど困難であり、そのことが「鍵」の安全性の原理になっています。事実、わずか7桁の数である1234567も127×9721のように素因数分解に苦戦しました。
図書館にある雑誌Newtonの昨年8月号が「素数の神秘」という特集を組んでいて、そこに素数を使った「鍵」について分かりやすく解説してあります。興味がある方は是非ご一読を。
追伸
1234567で思い出しました。123456789人です。何の数字でしょう?
昔、私が駆け出しの教員だった頃、新聞の見出しにこうありました。「日本の人口、今日123456789人」
いつの頃だったのかと改めてネットで調べたら、平成2年(1990年)4月3日のようです。ずっと増加傾向だった日本の総人口は、平成16年(2004年)12月の1億2783万8000人をピーク(総務省発表)に減少に転じています。減少のサイクルに入った日本の人口が再び123456789と並ぶのは2020年頃だと言われています。私たちはそのことを報じるニュースをどう受け止めるのでしょうか?
【校長】
手巻きウインチの設計図面がこんな形で!
いつも本校のHPにお越しいただきありがとうございます。
今日、学校は球磨工フェスタ(文化祭)を開催しています。あいにく、人吉市は産業祭を行っており、地域の中学校も文化祭をしているそうです。出足が心配されましたが、天気に恵まれたこともありお陰様で大盛況です。でも、中学生の皆さんにご観覧いただくことができなかったことは残念に思います。

私は昔、機械科の教師をしていました。前々々任校のことになりますが、3年間の機械科での学習の総まとめとして、卒業製図と称して描かせていたのがこの図面です。寒さに震えながら夜遅くまで描いていた生徒たちのことを思い出しました。
誰が描いた図面か知るよしもありませんが、将来こういう形で文化祭のポスターとして裏面が甦(よみがえ)るとはまさか思わなかったはずです。ある意味、機械科らしい究極のエコかもしれません。
話は変わりますが、体育館で行われた午前の部が終わり、校長室に戻りHPを開けたところ、今、午前11時24分現在の総アクセス件数は、1219957。
今日11月11日の日にちの数字の並びは1111で、レピュニット数(1がいくつも並んだ数字のこと。repunit【repeated unitの略】)です。
ということで、いつものように1219957に加減乗除等の記号を入れて、この1111を作ってみます。
121×9+√9×5+7=1111 → 11月11日
あまりにも簡単に出来たので手応えを感じません。もう一つ作ってみます。
√121+995+7!!=1111 → 11月11日
いくつも出来そうな気がします。皆さんだったらどんな式を作りますか?
【校長】
今日は古典の日

写真は一昨日、多良木高校であった会議に行った際に目にした校庭の木々をパシャリしたものです。さすがは奥球磨、人吉市内より色づくのが早いように思いました。
ところで、11月1日は「古典の日」。源氏物語千年紀を記念して10年前の平成20年(2008年)11月1日に京都で宣言されました。何とその2年後の平成22年、国の法律でも制定されました。
「こういうことが法律になじむのか?」と思えるような興味深い法律です。法文を読んだことがある方はきっと少ないでしょうから、全文を引用して紹介します。
(目的)
第一条 この法律は、古典が、我が国の文化において重要な位置を占め、優れた価値を有していることに鑑み、古典の日を設けること等により、様々な場において、国民が古典に親しむことを促し、その心のよりどころとして古典を広く根づかせ、もって心豊かな国民生活及び文化的で活力ある社会の実現に寄与することを目的とする。
(定義)
第二条 この法律において「古典」とは、文学、音楽、美術、演劇、伝統芸能、演芸、生活文化その他の文化芸術、学術又は思想の分野における古来の文化的所産であって、我が国において創造され、又は継承され、国民に多くの恵沢をもたらすものとして、優れた価値を有すると認められるに至ったものをいう。
(古典の日)
第三条 国民の間に広く古典についての関心と理解を深めるようにするため、古典の日を設ける。
2 古典の日は、十一月一日とする。
3 国及び地方公共団体は、古典の日には、その趣旨にふさわしい行事が実施されるよ う努めるものとする。
4 国及び地方公共団体は、前項に規定するもののほか、家庭、学校、職場、地域その他の様々な場において、国民が古典に親しむことができるよう、古典に関する学習及び古典を活用した教育の機会の整備、古典に関する調査研究の推進及びその成果の普及その他の必要な施策を講ずるよう努めるものとする。
附 則
この法律は、公布の日から施行する。
6年前、「古典の日」が法律で制定された時、マスコミでも大きく取り上げられました。当時、「えっ!何でまた法律で・・・?」と、私自身はかなり複雑な思いで受け止めたことを思い出します。
というのも、そもそも「古典の日」が京都で宣言された発端が、源氏物語の執筆千年を記念したものだったので、この法律でいう「古典」とはいわゆる国語で習う(文学の)古典とばかり思い込んでしまったからです。高校のとき、「ラ行変格活用」などでアトピーが出るほど苦しんだ古語文法を思い出し、「国は何と嫌な日を作ってくれたんだ!?」と思ってしまったわけです。
それから数年後、どういういきさつだったか忘れましたが、条文に目を通す機会がありました。第二条の「古典」の定義によると、文学だけでなく音楽や美術、演劇・・・と様々であり、「なんだ、そういうことだったんだ・・・(安堵)」と思った次第でした。
定義の後段には、「学術」や「思想」という言葉も出てきます。その視点から考えを巡らせてみると、今皆さん方が少なくとも普通教科で習っていることのほとんど、数学のサイン・コサインにしろ、理科のアボガドロ数にしろ、現社で学ぶベンサムの功利主義にしろ・・・、人類の叡智(えいち)の結晶であり、まさに古典といってもいいですよね。
私、そういうことも踏まえて、入学式の式辞に「古典」のことも触れることにし、毎年次のように話をしています。抜き出しておきますので、文中の「いにしえの賢人の思想」に着目しながら入学式の日を思い出してください。「そんな話、聞いたかな・・・」と思う人がいるかも?
・・・(前略)・・・第四次産業革命が社会や生活を大きく変えようとしている今、知識を得ることは勿論ですが、将来の技術者・技能者として数学的・論理的なものの見方や考え方をしっかり身に付けることは必要不可欠です。さらに、異文化やいにしえの賢人の思想に触れることで、自分の心の幅を広げ、それらを基に自分自身の頭で考え、判断し、実行する力も求められます。その意味で、中学までの教師や親から言われてする勉強から脱却し、知的好奇心を持って自ら学ぶ力を身に付けなければなりません。三綱領の中にある好学とはまさにそのような姿勢です。・・・(後略)・・・
話を大きく変えます。古典の日である今日11月1日に思いを込めて、朝一番(7時25分)にHPを開けた時の総アクセス数である1209199に加減乗除等の記号を入れて、日にちの数字の並びである111を作ってみます。
(120-9)×1(9-9)=111 → 11月1日
あっという間に式ができて拍子抜けです。生徒の皆さんだったらどんな式を作りますか?
【校長】
【注】 中学生の皆さんへ
102=10×10=100 とか 23=2×2×2=8 は御存じのとおりです。高校の数学では、もっとすごいものが出てきます。上に小さく書く数字を「指数」と呼びますが、この指数が0やマイナスのものが出てくるのです。
例えば、50とか、2-2という形のものです。
「0乗ってナニ?」「-2乗って・・・!?」
初めて見る人は、そう思うかもしれません。
それから、なんとこの指数、整数にとどまらず、有理数(二つの整数 a, b (ただしbは0 でない)をもちいて a/b という分数で表せる数)になることもあります。
64(2/3) とかです。3分の2乗とか、もう本当にすごい世界です。このように数の世界が広がることを「指数の拡張」と言うことがあります。
ちなみに、50は1、2-2は0.25、64(2/3)は16になります。
「・・・何で(?_?)」というのが実感かもしれませんが、高校の数学をお楽しみに。
ということで、今日の式の指数にあった(9-9)は0であり、1の0乗は1であることに注意しながら味わってください。
このように、どんな数も0乗すると1になります。今はそう覚えておいてください。勿論、高校ではなぜ0乗が1になるのか説明できるようになるはずです。
最後に・・・、今、「どんな数も・・・」と書きましたが、00(0の0乗)については、「0に0をかけると0だが、0の0乗は1である。果たして??」といった議論になることがあります。このことを理解するためには、高校の数学も越える高度な数学の素養が必要かもしれません。
祝 総アクセス数 120万件達成
いつも本校のHPにお越しいただき、ありがとうございます。
10月に入り、1日当たり平均1100件のアクセスをいただきながらカウンターは順調に数を伸ばしていました。

百二十万! 久々にきりのいい数字です。こういう綺麗な数字を見ると無性に素因数分解をしてみたくなります。早々やってみます。
1200000=27×3×55
従って、その約数は、1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 25, 30, 32, 40, 48, 50, 60, 64, 75, 80, 96, 100, 120, 125, 128, 150, 160, 192, 200, 240, 250, 300, 320, 375, 384, 400, 480, 500, 600, 625, 640, 750, 800, 960, 1000, 1200, 1250, ・・・(途中省略)・・・, 60000, 75000, 80000, 100000, 120000, 150000, 200000, 240000, 300000, 400000, 600000, 1200000
の96個あることになります。
では、いつものように 1200000 という数字の並びをそのままにして、加減乗除等の記号を入れて、今日の日にち10月24日の数字をそのまま並べた1024を作ることに挑戦してみます。
1×2(0!+0!+0!+0!+0!)!!!=1024
【注】 中学生の皆さんへ。”!”は、高校で学習する内容ですので、こうやって何度も説明していますが、”!”は「階乗」または「ファクトリアル」と読みます。
例えば5!なら、5×4×3×2×1を計算して120になります。
そして、0!=1というのも知っておく必要があります。これは定義(決めごと)ですから「どうしてそうなるの?」なんて考えたらいけません。
そういうことで、指数部にある(0!+0!+0!+0!+0!)の結果が5になる所までは大丈夫だと思います。
問題は”!!!”です。これは「3重階乗」といいます。このことについては、昨年の8月2日の記事以来、何度か解説していますが、このような「多重階乗」は、高校の数学の範囲も超えますので、「2重階乗(ダブルファクトリアル)」や「3重階乗(トリプルファクトリアル)」から順を追ってもう一度おさらいをしておきます。決して難しいものではありません。ついて来てください。
・まず、2重階乗(!!)は階乗の1つ飛ばしバージョンと考えてください。
n!!なら、n×(n-2)×(n-4)×・・・×・・・というように、2つずつ減らしながら掛け合わせます。nが偶数だと×4×2で終わりますが、nが奇数だと最後は×3×1で終わることになります。5を例にとってやると
5!!=5×3×1=15 となります。
・3重階乗(!!!)は階乗の2つ飛ばしバージョンと考えてください。
従って、5!!!なら、2つおきの階乗ですから、5×2で10になります。
要は、210=1024 を作ったわけです。2を10回かけると1024、これはとても有名であり、覚えておいて損はありません。
ちなみに、高校に入学して1年もしくは2年生で学習する専門の基礎科目に情報技術基礎という科目があります。その中にコンピュータで用いられる単位であるビットとバイトを扱う単元があり、この1024という数字が登場します。
コンピュータでは、2進数を扱う都合からキロ(K)やメガ(M)といった接頭辞が1000ではなく1024のべき乗で表示します。例えば、1 KB=1024 B、1 MB =1024 KB となります。つまり、1024Bが1kB、1024KBが1MB、1024MBが1GB、1024GBが1TB・・・となります。
簡単に言いますと、2進法で表すコンピュータの世界での1つの単位の大きさは、1024倍ごとに上がっていきます。高校の授業をお楽しみに・・・
ということで、「毎月120万円のお給料があれば(経済的には)幸せだろうな・・・」なんて思いつつ、あくまでも仮定の妄想をしながらこの数字と遊んでみました。
【校長】
「よけまん」って?
いつも本校のホームページにお越しいただきありがとうございます。

生徒の皆さん、頑張ってください。
ところで、学校からちょっと郊外に足を向けてみると、球磨川沿いに広がる田んぼでは、稲の穂が重そうに垂れています。
秋まさにたけなわ。
この光景を見ていると、「実るほど頭を垂れる稲穂かな」という言葉を思い出しました。色々な話でよく引用されますので、きっと生徒の皆さんも聞いたことがあると思います。稲の穂は実るほどに穂先が低く下がるわけですが、人も社会的な立場が高くなればなるほど、謙虚な姿勢で人と接することが大切であるという教えです。(私自身はこの言葉、パナソニックの創業者松下幸之助氏の「人生談義」という本の中で知りました)
稲と言えば・・・
お隣の高校、南稜高校のHPの昨日の記事が印象的でした。「南稜米の調製が終わりました!」というタイトルのブログの中に、調製作業が終わった南稜米を冷蔵庫へ運ぶ様子が写真付きで載っていました。今年は豊作だそうです。お米が一杯に詰まった100袋もの米袋をトラックから冷蔵庫まで運ぶのは、本当に大変だったみたいです。実際、とても難儀そうに運んでいて、袋を担ぐ生徒の表情に重さが滲み出ていました。
その記事の中に気になる言葉を見つけました! 次の一文です。
「重い、重い」と言いながら持ち方を工夫して運びました。終わった後、「よけまんがあればいいのに」と。確かに(笑)
私、「よけまん」という言葉を初めて目にしました。何人かの先生に聞いたところ御存じないようでしたので、「きっと方言に違いない!」と思って検索してみました。
やっぱりそうでした。あるサイトに、次のように紹介されていました。
この言葉の意味を知ってる方は、相当ディープな熊本人か、熊本オタクですね!「よけまん」とは、主に球磨地方に伝わる方言で、おやつ とか、一息入れる という意味です。よける(避ける) と おまんま がくっついて、「よけまん」となったそうで、「田んぼや畑での農作業を休憩して、おやつで一息いれる」という、意味合いなんだそうです。でも、昔むかしの言葉ではなく、球磨では今も立派に、普通に使われてるんですよ。・・・(後略)・・・
ディープな熊本人とか熊本オタクというコメントが何とも面白く可笑しいです。
それはさておき、農業系の高校は血が通う生き物を相手にしているので、工業高校とはまた違った学校の日常があり、ブログの内容もバラエティに富んでいます。同じ高校生として、隣の高校に通う友がどのようなことを学んでいるのか、他校のHPもちょっとのぞいてみてはいかがでしょうか。
【校長】
球磨工の情報を発信中!
リンクはこちらから
学校情報
〒868‐8515
熊本県人吉市城本町800番地
TEL 0966-22-4189
FAX 0966-22-5049
E-mail
kuma-th@pref.kumamoto.lg.jp
熊本県教育情報システム
登録機関
管理責任者 校長 坂本道彦
運用担当者 ホームページ係