徒然雑記帖
胸がざわつく17歳
今日2月22日は、「ニャン(2)ニャン(2)ニャン(2)」の語呂合わせから、「猫の日」に制定されていると朝のニュースで報じていました。この日をきかっけに、2月は全国各地で猫にちなんだイベントが開催されて、猫好きにはたまらない月なんだとか。
考えてみれば、月日をその順に並べた時、同じ数が3つ連続するのは1月11日の111と2月22日の222の2つだけです。万一、333とかあったら超気持ち悪いよな・・・とか考えていたら、今日は総アクセスカウンターに、2が沢山出現するということに気付きました。1312222という数字です。
午前7時頃からカウンターを見守っていました。多分、7時18分頃通過したはずです。
さっそく1312222で今日の日付の222を作ってみることにします。
1-3+1×2+222=222 → 2月22日
(13+1)×222÷2=222 → 2月22日
どちらも下4桁の2222を使っただけの面白みに欠ける式で、「小町算を舐めているのか!」と叱られるかもしれません。
気を取り直して、今日が誕生日の本校生が何人いるのか、名簿に検索をかけてみました。561人在籍しているから確率的に1人以上は期待できます。
1人いました。今日17歳を迎えた方、おめでとうございます。何か特別な感慨がありますか?
我が国も3年後の2022年4月から、成人年齢が20歳から18歳に引き下げられることが決まっています。その頃には、大人になる寸前の17歳という年齢は、今の19歳以上に輝きを増しているのかもしれません。
ところで、2年生の大半は既に17歳のはずです。今、その真っ最中を主人公として過ごしている皆さん方には、実感があまりないかもしれませんが、17歳というのは大人が昔を振り返ったとき印象深く刻まれている年齢だと思います。映画や文学など様々な作品でも17歳というのはよく取り上げられていていますし、大阪経済大学は「17歳からのメッセージ」という随筆コンクールを主催しています。Seventeenという女性向けのファッション雑誌もありますよね。
48年も前の話になりますが、南沙織さんというアイドル歌手のデビュー曲は「17才」*でした。私、この曲を希に耳にすると、自身が17歳のころ、どんな景色を見ていたんだろうと胸がざわつきます。(でも、残念なことに先日、2月7日の記事で取り上げた「ワンちゃん事件」以外あまり思い出せません)
大人と子どもの間で揺れる曖昧な時である17歳、きっと皆さんもずっと後になってからそのキラキラに気づくのかもしれません。
自分はどういう人間なのか、大人になるとはどういうことか、どのような大人になりたいのか、将来どんな仕事をしてどんな働き方をしているのか・・・そんなことに想いを巡らして17歳の今の自分の考えを文章にまとめておくのも有意義なことかもしれません。
【校長】
*南沙織さん、昭和46(1971)年に、この曲でデビューして1ヶ月後に17歳になったそうです。当時、テレビやラジオからやたらに流れていました。年末に日本レコード大賞(新人賞)を受賞して、紅白歌合戦の紅組トップバッターだったこと、私は小学5年生でしたが、「歌謡曲大好き少年」でしたからよく覚えています。
軽やかなメロディーも詞もどちらも好きでしたが、今にして思えば「17才」という言葉が歌詞の中に出て来ない不思議な曲だと思います。ウィキペディアによると、作詞家の有馬三恵子さんが作詞したのは既に40歳前後だったため、この曲がヒットしたときは周りから「40歳になってよくあのような詞が書けたね」と、半分呆れられるかように誉められたとあります。心温まるいいコメントです。それほど詞の内容が当時としては鮮烈だということだと思います。
小学生の私には、高校生のお姉さんの恋愛事情は眩しすぎましたが、しっかり感情移入して口ずさんでいました。ませガキだったんだと思います。多分。
その後、色々な歌手がカバーしていますので、きっと皆さんも聞いたことがあるはずです。
こめかみには夕日のうず
学校は昨日から学年末考査が始まりました。1年を締めくくる大事な試験です。全力を尽くしてください。
ところで、先日の3連休、寒い日々が続きました。生徒の皆さんは勿論、試験勉強に明け暮れていたはずですが、私は10日(日)に今年初めて金峰山(熊本市:665m)に登りました。南区島町の自宅から熊本西高校の横を通り過ぎて、河内町の手前から右折するコースで、片道17km位です。下山中の午後6時頃、雲仙普賢岳の横、島原半島に夕日が沈んでいました。あまりにも綺麗だったのでスマホでパシャリ。
夕暮れは、古来詩情をかき立てるようです。百人一首には収められてないけど「三夕(さんせき)の歌」と呼ばれる名歌があると昔、カルタ部の指導をしていた時、何かの本で読んだことがあります。さっそく調べ直すと・・・
さびしさは その色としも なかりけり 真木立つ山の 秋の夕暮れ (寂蓮)
心なき 身にもあはれは 知られけり 鴫立つ沢の 秋の夕暮れ (西行)
見渡せば 花も紅葉も なかりけり 浦の苫屋の 秋の夕暮れ (藤原定家)
いずれも新古今和歌集に採られた歌で、三句目を「けり」(詠嘆)で切り、五句目を「秋の夕暮れ」(体言止め)で結んでいます。最初の寂蓮法師の歌は意味がちょっと取りにくいですが、下2つは口語訳がなくても、今を生きる私たちにも寂寥とした景色が思い浮かんでくるほど分かりやすいはずです。秋の夕暮れの美しさと侘しさを愛でる心は日本人のDNAなのか、今も昔も変わらないと言ってもいいかもしれません。
とは言っても、夕暮れの捉え方も色々あるようでビックリです。「理系の人々」という理系へのイメージや偏見を面白おかしく描いたコミック本があります。本校の図書館には収蔵してありませんが、映画化もされているぐらいですから読んだ方がきっといるはずです。その中に「夕日」を巡って、太陽が沈むと、太陽光が通る大気の長さが長くなり、その結果、可視光線の青以外にも波長の短いその他の色も散乱してしまい、最終的に最も波長の長い赤色が目に飛び込んでくるという当然の現象が起こるだけで、なぜ文系の人たちがそんなに心を動かされるのかよく分からない・・・といった自虐?ネタで展開するストーリーがありました。私も理系の端くれのつもりですが、そこまで醒めた目で夕日を眺める人たちがいるとは…、いやはやです。
やはり、秋の夕暮れに真っ赤な太陽が沈んでゆくのを眺めながら、その瞬間に自分の二度と反復できない生の一回性に深く思いを致すだろうし、もしその隣に大切な人がいなかったら写メを送ってでもその光景を享有したいという気持ちがわき上がる(これらが文系の人たちの一般的な思考パターンなのかよくわかりませんが)のは当然だと思うし、どちらかというと私はそういうタイプです。
と言うことで、私にとって夕暮れは、中森明菜さんの名曲「トワイライト~夕暮れ便り~」が条件反射です。夕日を見るたびにタイトルに記したイントロ部を口ずさんでいた昔もありました。
私と同年代の方にとっては多分懐かしく思い出すであろうこの曲、大学を出て大阪の民間企業に就職した翌年、1983(昭和58)年にヒットしたもので、作詞が来生(きすぎ)えつこさん、作曲が来生たかおさんの姉弟による作品です。生徒の皆さん達にとっては、生まれる前の話ですから知らない人が多いかも?ぜひyoutubeなどで聴いてみてください。以下の話を納得してもらえるはずです。
「三夕の歌」のついでに、なぜこの曲について触れようと思ったかというと、昨夜、学校から帰ってラジオをかけて寛いでいたら、バレンタイン特集を締めくくる最後の曲として流れてきたからです。本当に久々に聴きました。私、懐かしさで思わず、読みかけの本を落っことしてしまいそうでした。
『や~はり あ~なたと 一緒に居たい 一言かきあぐね ・・・・・ 感じますか 届きますか この黄昏と恋便りまでも♪』
私は以前から、山口百恵さんの「いい日旅立ち」など、静かに愛する人のことを思いつめるバラード系が大好きでした。この「トワイライト」もその一つです。twilightとは、本来、黄昏(たそがれ)時、日の出前や日没後の薄明かりを意味します。初めて聞いた時、曲想自体もしみじみとして涙が出そうになったのですが、詞に対して何と素敵なタイトルをつけたんだろう思いました。でも、印刷された詞だけ読んでも、どうって事ありません。「好きな人に自分の想いを届けるために手紙を書く」、ただそれだけのことを綿々と大げさに表現しているだけです。しかし、曲が詞とあいまって盛り上がる、この効果は絶妙です。また、「一筆書く、手紙を書き送る」を英熟語でdrop a line と表記することがすんなりと腑に落ちる曲でもあります。
きっとこの曲の主人公は、恋も失恋も色々経験して、一人でいる時に美しい景色を見て、好きな人に思いを馳せることを何度もしたのかもしれません。一言一言がグッと胸に突き刺さるだけでなく、海辺の清涼感と黄昏の残照も感じさせる抒情的な名曲だと思います。もし、西行や定家が生きていたら、この曲をどう評するのか興味深いところです。
話は大きく変わりますが、若い頃の私にとって、中森明菜さんはリリースする曲ごとに「ウ~ん」「エッ!」と、思いが交錯した不思議な歌手でもありました。
デビュー曲「スローモーション」、来生姉弟の曲です。思春期のときめきを感じさせる清純なイメージ。その可愛らしさを打ち砕く「少女A」。これって不良賛歌?騙された!と思う間も無く、またしても来生姉弟の手による「セカンドラブ」。私の十八番。切ない系のバラードでやっぱり根はいい子だったんだ、とか思っていたら「二分の一の神話」で「いい加減にして〜!」と絶唱。これって突っ張りそのもの?そして「トワイライト~夕暮れ便り~」でしみじみと。どれが本当の明菜さんなのか、本校生の中にもこういう二面性を巧みに演じ分けることができる人がいるのでしょうか?
最後に・・・、かつて大阪と札幌を結ぶ「トワイライト・エクスプレス」というJR西日本が運行していた寝台特急列車がありました。出発時の夕暮れと到着時の明け方のそれぞれの時の薄明かりのイメージが命名の由来と聞いていましたが、実際に乗車して、日本海に沈む夕日などを車窓越しに眺めて納得しました。大阪駅を出発してすぐの車内放送の出だしにかかる音楽が山口百恵さんの「いい日旅立ち」で、いやがうえでも旅情が高まり、そういう意味で凝った演出をしていた列車でした。
もう一つ。明菜さんは私より6つ年下のはずだから今は何歳なんだろうかと指を折ったりもします。心の中では80年代のアイドルのまま(そういう意味ではこの記事の中で「明菜さん」は「明菜ちゃん」と表記したかった)です。でも、みんな平等に1年に1つずつ歳をとります。トワイライト(twilight)には、人生の黄昏即ち終末期の意味もあります。本を落っことすほど反応してしまったのは、心だけは若者のつもりでも、そ~っと人生の晩年が忍び寄ってきている証拠かもしれません。
【校長】
The 45th memorial day of the school piano
本日2月14日は、本校体育館にあるグランドピアノの45回目のアニバーサリーです。昭和49年(1974年)の今日、学校に設置されたと備品台帳に記録されていました。当時の価格で41,9700円。ネットで調べたところ、当時の高卒の初任給の平均(製造職)が約24,000円位、現在が約16,2000円ですから7倍弱、それを目安に現在の価格に換算してみると300万円位になります。グランドピアノを42万円で買い求めることは、今なら中古でもできませんが、こうして物価の違いを考慮すると、きっと中古ではなくて新品だったのでしょう。
本校を6年前に御退職になった江嶋先生に電話でお尋ねしたところ、校歌の作曲者でもある電気科の塩田靖弘先生が御在職中は、先生の御指導の下、生徒の伴奏で卒業式や入学式があっていたそうです。しかし、平成4年(1992年)に先生が御退職になった後は弾く生徒がおらず、体育館のステージの片隅で部活生のジャージ置き場として使われていたようです(園田先生談)。以来、多分ボールがぶつかるなど、ピアノにとっては苦難の日が続いたのかもしれません(涙)。先日点検したところ、鍵盤が上に戻ってこないなど不具合が沢山見つかり、急遽、修理と調律を行いました。
なぜ26年ぶりにピアノを長い眠りから起こしたかというと、(既に耳にしている人がいるかもしれませんが)今度の卒業式の式歌(君が代・校歌・蛍の光、仰げば尊し)は、なまのピアノ伴奏のもとで歌ってもらうことにしたからです。「伴奏してもいいですよ」と申し出てくれたのは、電気科1年の日下部(くさかべ)快生君と建築科1年の谷口純美さんです。
2人には、写真のようにボール等が当たらないようにバリアでしっかり囲ったピアノで、昼休みと放課後の少しの間、練習をしてもらっています。歌はみんなで歌いますが、伴奏は1人です。緊張のあまりミスタッチをしたとしても止まらずに歌に合わせて弾き続けることや、万一止まったとしても途中からでも(どこからでも)弾き始める力が要求されます。その意味で伴奏者には演奏技量は勿論、襷を繋ぎ続けていく駅伝選手と同じくらい強靱なメンタルが求められます。卒業式当日、素晴らしい伴奏で卒業生・在校生みんなと校歌等を高らかに歌えるよう練習を頑張ってください。
バレー部やバスケットボール部等、体育館内で練習している部活動の皆さんには、少々お邪魔になるかもしれませんが、御理解をお願いします。
【校長】
祝 総アクセス数 130万件達成
いつも本校のHPにお越しいただき、ありがとうございます。
1月に県立学校のHPシステムの更新が行われ、それ以降なぜかアクセスカウンターが伸び悩むという現象が続いています。
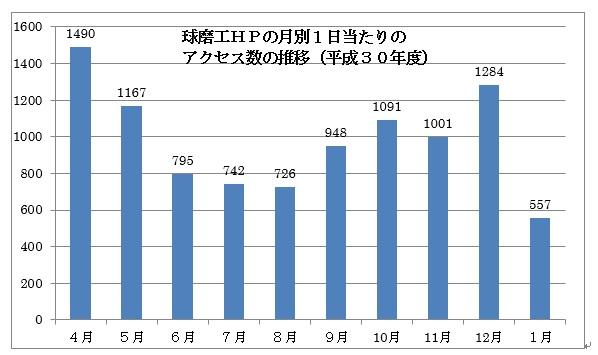
実際、今年度4月からの月別の1日当たりのアクセス数をグラフ化してみると、下のように推移しており、一目瞭然です。1月は12月に比べて半減してしまいました。
高速道路を走る大型トラックには、速度抑制装置(スピードリミッター)の装着が義務づけられて事実上90キロ以上出せないようになっているそうですが、いつの間にかアクセスカウンターにそのような抑制装置が付けられたのか(勿論そんなことはないはずですが)、まるで鉛が付いているかのように鈍い動きにそんなことさえ思ってしまいます。スランプは誰にでも突然訪れることと同じなのかもしれませんが・・・。
ということで、12月のペースなら1月の中旬にとっくに実現していたであろう130万件、やっと達成です。

130万! 久々にきりのいい数字です。
こういう綺麗な数字を見ると無性に素因数分解をしてみたくなります。早々、やってみます。
1300000=25×55×13
従って、その約数は、
1, 2, 4, 5, 8, 10, 13, 16, 20, 25, 26, 32, 40, 50, 52, 65, 80, 100, 104, 125, 130, 160, 200, 208, 250, 260, 325, 400, 416, 500, 520, 625, 650, 800, 1000, 1040, 1250, 1300, 1625, 2000, 2080, 2500, 2600, 3125, 3250, 4000, 5000, 5200, 6250, 6500, 8125, 10000, 10400, 12500, 13000, 16250, 20000, 25000, 26000, 32500, 40625, 50000, 52000, 65000, 81250, 100000, 130000, 162500, 260000, 325000, 650000, 1300000
の72個あることになります。
一桁目が5で終わる奇数の約数が全部で10個(約14%)ありますが、どれも「当然、あり得るよね」という約数ばかりで、以前、888888が77や777を約数に持つことに気付いた時に味わったような高揚感はありません。
では、いつものように 1300000 という数字の並びをそのままにして、加減乗除等の記号を入れて、今日の日にち2月7日の数字をそのまま並べた27を作ることに挑戦してみます。
13×(0!+0!)+0!+0!-0!=27 → 2月7日
1+30-(0!+0!)×(0!+0!)=27 → 2月7日
今回は、0!=1という定義(決め事)を使って簡単に2つできあがりました。
最後に・・・、生徒の皆さんは130万と聞いて、何か思い浮かぶことがありますか?
もし、お父さんが会社員、お母さんがパートで月10万円前後を稼いでいるご家庭だったら、130万という数字はお茶の間で時々話題になっているはずです。いわゆる「130万円の壁」です。税金や社会保険料の支払いで損しないためにも注意しておかないといけない数になりますが、まだまだ皆さんには早いかもしれませんね。気になる人は調べてみてくだい。なぜこういう制度があるのか知るところから、社会の仕組みが見えてくるかも?
【校長】
仮定法の思い出
トランプ大統領の5日の一般教書演説、いまだにメキシコ国境に壁を建設する公約の実現に強い意欲を示していることなどがテレビ等で盛んに報じられ、生徒の皆さんもきっと耳にしているはずです。
今朝7日の朝刊各紙にはその和訳が載っていました。讀賣新聞には、演説のポイント部分について英文が載っていたので、何気に目を落としてみました。
If I had not been elected President of the United States, we would right now, in my opinion, be in a major war with North Korea.
私が米国の大統領に選ばれていなかったら、私の意見では、今まさに、北朝鮮と大規模戦争になっていただろう。
たまたま読んだ大統領の英文、仮定法でした。「英語中級者の壁」とも言われるこの構文、私も高校の頃、散々苦労したことを思い出します。
手元のシラバスによると、本校では3年生の「コミュニケーションⅡ」で3学期に仮定法過去や仮定法過去完了について学習するようです。誰が名付けたんでしょう。名前がいかめしいですよね!「仮定法過去完了」って。この大統領の英文、まさにその「仮定法過去完了」かと思いきや、if節が仮定法過去完了、主節が仮定法過去という高校生泣かせのあの恐ろしい構文でした。
私が仮定法について学んだのは高校2年生の頃です。「英語では仮定の話をするとき、なぜ一つ前の時制を使うのか」、多分そんなことだっただろうと思い出すのですが、先生が熱心に説明していました。
その時、私は教室の廊下側の一番前の席で、開けっぱなしのドア越しに廊下の向こうから校舎に迷い込んだ仔犬がこっちに来るのが見えました。私と目が合うと突然立ち止まったので、「どこから来たの、お腹すいたの・・・?」とか口パクでしゃべってしまいました。当然、先生に見つかってしまい、「授業に集中してない!」とこっぴどく叱られ、怒り狂った先生が何とそのワンちゃんの首根っこを掴んで校庭に追い出してしまいました。私にとって仮定法はそんな苦い思い出と一緒に甦る構文でもあります。
そういうことを思い出しながら、今一度大統領の英文と和訳を読んでみたら、エッ?和訳がひょっとして間違っているのでは?と気付きました。
讀賣といえば、日本を代表する大新聞です。校閲はしっかりしてあるはずで、そんなことはまずあり得ないはずですが・・・。でも、right now が挿入され、「今まさに」とあるわけですから、当然文末は現在形で訳し、次のようになるべきではないかと思います。どうなんでしょう。生徒の皆さんはどう思いますか?
私が米国の大統領に選ばれていなかったら、私の意見では、今まさに、北朝鮮と大規模戦争になっているだろう。
【校長】
大きく変わりつつある高校入試
ここで述べることは1月21日にアップした「大学入試が変わる」と関連があるというか、その続編になることを最初にお断りしておきます。
私、教師になって以来、本校生は一体どういう問題を解いて入学してくるのかという観点から、高校入試の問題を毎年、結構時間をかけて眺めています。そして「最近、変わってきているな・・・」とつくづく思っていることが3つあります。
1つ目です。統計を取って分析しているわけでは勿論ありませんが、「平清盛は中国の( )との貿易に力を入れた」というような単なる知識・理解を問う穴埋め問題に代わって、記述式で「思考力・判断力・表現力」を問う問題が年々増加傾向にあることを実感しています。その記述量自体も増えているのは間違いないはずです。例えば、昨年度の社会科の問題では記述式が8問出題され、新聞に掲載された正解例に示された文字数の合計は、句読点まで含めて208文字にのぼります。過去数年分の5教科の総記述文字数は、一体どう推移しているのかグラフ化してみると、きっと顕著な傾向が見えるはずだと睨んでいます。
昔から証明が定番の数学は勿論のこと、国語や英語だけでなく、最近では理科や社会科でも、因果関係を説明させるものや、資料やグラフ・図表などを読み取って記述させる問題などが盛んに出題されています。しかも、解答を引き出すまでに読まなければならない資料や問題文がとにかく長くて多く、短時間に的確に自分の考えをまとめるためには相当な思考力や表現力が問われます。日頃から授業に主体的に臨んでおくことは勿論、様々なジャンルの本や新聞等を読んで自分の見識を深め、社会の動きにも関心を持っておくことが必要だと痛感します。
2つ目は、1つ目で述べた「思考力・判断力・表現力」を問う記述式の問題が多く出題されるようになっていることから当然言えることですが、難化傾向にあるということです。
私は専門が機械ということもあり、数学と中学生の頃から苦手だった「月」の問題を除いた理科だけは毎年全ての問題に挑戦しています。数学で例年出題されている二次関数と一次関数を組み合わせた問題や図形の融合問題(B問題)の中には、片手間では解けず、自宅に持ち帰って考え込むような問題がこのところ必ず1問はあります。誰がこんな難しい問題を作ったんだろう、この問題が時間内に解ける受験生がいるんだろうか、ひょっとして宇宙人?と思うほどです。そういう超優秀な頭脳の持ち主を早期に把握して、次のステップに向けて入学後の指導計画を立てるというのも高校にとっての難問の役割なのかもしれませんが・・・。
3つ目は、設問の中で「会話形式」で進めていくパターンが著しく増えているということです。「対話」の強調は、「主体的・対話的で深い学び」を求める次期学習指導要領を貫くキィ・コンセプトでもあるわけですが、具体的には、初めにある事象や実験が示され、これに対して数人が話し合いを進め、考察し、その過程の中に問題を組み込むパターンです。
例えば、昨年度の理科の問題では、由香さんと卓也君の会話が次のように出題されていました。
由香:・・・・の河原で安山岩が見えたのはなぜかしら。
卓也:・・・・を考えるとわかるかもしれないよ。・・・・・も興味深いね。
由香:・・・・についても、もっとくわしく調べたいね。
「~かしら」って女性語?かなり無理をして作問したようで、思わず「かわいいな・・・♪」とニヤケてしまったのは私一人ではないはずです。(「俺は・・・」で始まる会話はついぞ見たことがありません)
それはさておき、この手の問題は私たち教師に、「子どもたちに考えさせる授業をしていますか?」というメッセージを投げかけているように思えてなりません。
昨年度の社会科では、授業の一場面を扱った会話を元にした問題が出題されました。それをよく読んでみると、「先生」は何も知識を与えていません。ただ話題を提供して、答がある方向に誘導しているだけです。少々知識のある大人であれば、子どもに解き方を見せたり、答を与えたりすることは簡単です。しかし、そんなやり方ではダメだと言っているようにも思えます。
中国には、「飢えている人に魚を与えると喜ばれるが、その場しのぎにしかならない。それよりも魚の釣り方を教えてあげることがその人のためにはなる」といった趣旨の老子の言葉に由来する格言があります。確かに、人に魚を与えても1日で食べてしまい、釣りを教えれば一生食べていけるわけですが、この格言は教育の現場でもしばしば引用され、まさに言い得て妙です。授業も一緒。授業が単に勉強を教える場となってはいけません。こうした入試問題は、「人生の課題解決の知恵を子どもたち自身が獲得できるような授業が求められている」ということを暗示しているようで、厳粛に受け止めなければならないと思っています。
話は変わりますが、1月21日の記事で触れた大学共通テストのプレテストでも、生徒と先生の会話、生徒同士の議論といった「会話形式」の中での問題がほぼ全ての科目にありました。次は、平成30年の数学Ⅱ・数学Bの問題です。
花子: これは前に授業で学習した漸化式の問題だね。まず,・・・・の形に変形するといいんだよね。
太郎: そうだね。そうすると公比が・・・・の等比数列に結びつけられるね。
花子: 求め方の方針が立たないよ。
太郎: そういうときは,・・・・を代入して具体的な数列の様子をみてみよう。
花子: ・・・・となったけど…。
太郎: 階差数列を考えてみたらどうかな。
「こういう数学的会話が教室で本当に展開されるのかな?」「正直、こんなに物分かりのよい生徒はいねぇよ!」といった受験生の斜に構えたような感想も多数あったようですが、共通テストも高校入試も、形としては全く同じ傾向です。結局、大学入試が変化しているので、高校入試も変化していると考えるのがもっとも自然といえるでしょう。
そのような思いで大学入試センターのHPに公開されているプレテストの問題を改めて眺めていて面白いことに気付きました。
作問の在り方をつくづく考えさせられます。「超駄」かもしれませんし、少々長くもなります。お暇な方はおつきあいください。これは、平成30年のプレテストの国語の古文の問題の最後の設問です。源氏物語からの出題でした。以下に抜粋します。なお、○○や△△、・・・などは、それぞれコッテリした文言が入っていますが、この問題を考える際には全く関係ないので省略しています。
二重傍線部の解釈として、会話の後に六人の生徒から出された発言のうち、適当なものを二つ選べ。ただし、解答の順序は問わない。
生徒A: 私は○○だと思います。
生徒B: そうかなあ。私は△△だと思います。
生徒C: 私はAさんの意見がいいと思う。つまり・・・ということになるね。
生徒D: 私もAさんの意見でいいと思うけど、✕✕に関してはCさんとは意見が違って・・・・。
生徒E: いや、私はBさんの意見ほうが正しいと思うよ。・・・だから。
生徒F: 私もBさんの意見のほうがいいと思う。でも、・・・だよ。
「これって本当に対話だろうか?」、そのような思いはとりあえず置いておき、単純な組み合わせの問題と捉えると、6C2で15通り(AとB、AとC、AとD、AとE、AとF、BとC、BとD、BとE、BとF、CとD、CとE、CとF、DとE、DとF、EとF)の組み合わせが考えられます。
ここで、話の流れを吟味してみます。まず生徒Aと生徒Bが大きく2つの異なる見解を出して、それに対して生徒A側に賛同する立場から、生徒Cと生徒Dが異なる見解を補足しています。同様に生徒B側に賛同する立場から生徒Eと生徒Fが異なる見解を補足しています。そのことは、・・・等で本質的な所を抜いたこの会話からでも見抜けます。
Aの意見に賛同しているのはCとDであり、Bの意見に賛同しているのがEとFであることを考えあわせると、まずAとBで大きな二者選択になってしまうので、AとBの組み合わせを即削除、そして、AとE、AとF、BとC、BとDの4通りも論理的にあり得なくなり、すぐに除外が可能です。
同様に考えると、CとD、EとFも矛盾しているし、CとE、CとF、そしてDとE、DとFもヘンな組み合わせとして除外できます。
結局、AとC、AとD、BとE、BとFの4通りのうちどれかという問題です。実際、この問題の正解は、BとFです。
よ~く考えるまでもなく、二重傍線部の解釈を誤り、最初の選択であるAかBの選択を誤るとAとCやAとDを選択しかねず、その場合全滅してしまう可能性があります。この問題の配点は1問7点であり、2問で14点という今回の国語のプレテストの中では最大の配点になっていました。14点ゲットできるか0点か、この差は実に大きいと思います。こんなときは、「矛盾していることは重々承知でAとBを選ぶと7点は確保できるんじゃ?」とかやけくそ気味に考えた受験生がいたかもしれません。
そういうことで、生徒たちが対話や議論する問題で思考力・判断力等を問う問題を作問するのは、難しい一面があると考えさせられたところでした。
【校長】
What is your belief?
1月最後の週が始まりました。3年生は今日が最後の授業日、そして明日から学年末考査です。3年間の集大成の試験になります。全力で取り組んでください。
ところで、先週の週末、特に26日(土)は、時折雪が舞う大変寒い一日でした。生徒の皆さんはどのようにお過ごしでしたか?
私は当日、九州ルーテル学院大学で開催された「英語スキットコンテスト」の応援に行きました。今回で3回目になるこのコンテスト、県内の公立、私立高校から合計46チームが出場し、本校からもA、B2チームが参加しました。
スキット(skit)とは、「寸劇」を意味します。参加者2〜3人で構成する1チームが英語の台詞による寸劇(3分以内)を行い、内容・演技・英語による3つの基準で得点を競う方式で実施されました。
今回のテーマは、"belief"(信念)です。「あなたの『信念』は何ですか?」と、いきなりマイクを突きつけられたら多くの人がたじろぐと思います。心の軸とも言える「信念」、これを3分以内でどうコミカルにまとめるか、演技力や英語力の前に劇の構想力が問われます。
Aチーム(星原夢杜【1MB】君・平川皇樹【1MB】君・玉村慶太【2MA】君)は、"The world of AIs and human beings"のタイトルで、AI(人工知能)と人間がものづくりの大会で勝負します。その結果はいかに?
Bチーム(中島洸志【1AT】君・畑早和【1AT】君・段村冷美【2AT】さん)が演じたのは、宮大工を目指し日々技術の修練に励む高校生が、前が見えない壁にぶつかっているという設定です。そこに通りかかった同級生が・・・・。タイトルは、"Where there is a will, there is a way"(「意志あるところに道あり」の意味)で、ある意味"belief"の言い換えと言っていいかもしれません。
それぞれ、生徒たちが頭をひねって考えたシナリオと聞きました。一月ほど前、シナリオを読ませてもらったときから、「実に工業高校生らしい着想で面白い!」と、ずっと期待していました。
本番はミスなく、練習してきた最善の演技を多くの観衆と審査員の前で披露することができました。周りの先生方からの感想も好評なようで、ワクワクして結果を聞きましたが、残念ながら2チームともに決勝コンテスト進出は叶いませんでした。会場を後にしようとしたとき、「非常にメッセージ性のある、いいスキットだと思った。そのことを是非お伝えしたかった」と、わざわざ言いに駆けつけてくださる他校の先生もいて、嬉しく受け止めたところです。
次回大会での決勝コンテスト出場と上位入賞を目指して、また新たな取組みが始まることでしょう。他の球磨工生にとっても良い刺激となること間違いありません。私、残念なことに英語がよく聞き取れず半分も理解できませんでしたが、表情豊かにプレゼンテーションをする高校生たちに圧倒される半日になりました。
英語科の先生方には毎日遅くまで御指導いただきました。大変お世話になりました。また、保護者の皆様には応援ありがとうございました。
【校長】
大学入試が変わる
本日から県立学校の前期(特色)選抜の出願が始まりました。前期選抜は、本校の各科に関する学習に興味・関心があり、意欲的積極的な志望動機を持つ受験生の中から、その多様な能力や適性、意欲や関心、努力の成果などの優れた面を積極的に評価して選抜するものです。願書を託された中学校の先生方が次々と手続きに訪れ、受験シーズンが本格化した感がします。
本校を目指す受験生の皆さん、体調に気をつけて頑張ってください。
ところで、昨日、一昨日と「大学入試センター試験」が実施されました。全国で50万人余りが受験したとあって、テレビ等でも大変大きく報じられました。その中で必ず言い添えられたことが、「センター試験は来年2020年1月実施(2021年度入学者向け入試)を最後に廃止され、2021年からは、『大学入学共通テスト』(新テスト)が実施される」というものでした。
今の高校1年生以下は、この新テストを受験することになります。
本校生の大半が就職を選択しており、進学では国公立系でも工業高校枠の推薦入学制度を活用している者がほとんどで、今年度はセンター試験を受験した生徒はいませんでした。しかし、昨年度、一昨年度それぞれ1人ずつではありましたが、受験生がいたことは事実です。「入試制度が変わる」という報に接し、高校1年生やその保護者、中には中学3年生やその保護者の皆様の中にも、漠然とした不安をお持ちになられた方も多いのではないかと案じております。
今日は、大学入試の試験内容等がどう変わるのか、本校としてどう対応しようとしているのかを簡単にご説明をします。
「グローバル化や第4次産業革命に対応しうる人材を育成するため、新しい学力評価制度・大学入試制度の設立が必要である」ということが、この入試改革の背景にあります。文部科学省HP内の「大学入学者選抜改革について」では、そのような人材育成のためには、「学力の3要素」である①知識・技能、②思考力・判断力・表現力、③主体性を持って多様な人々と協働して学ぶ態度、の3つを育成・評価することが重要であると記されています。
では、具体的に何がどう変わるのか。センター試験にはなくて、新テスト(共通テスト)に新たに導入・変更されるものが3つあります。1つ目が「記述式問題」、2つ目が民間の検定試験を活用した英語の「4技能評価」、3つ目は提出書類に「志願者本人の記載する資料」等が加わるなど「調査書等の見直し」です。
まず1つ目です。現行の「大学入試センター試験」は、正解を選択肢の中から選ぶだけの出題形式ですが、新テストでは記述式の問題も加わることになります。このことで、「自らの力で考えをまとめさせたり、相手が理解できるよう根拠に基づいて論述させたりすることで、思考力・判断力・表現力が評価できる」としています。また、高校や中学校では「主体的・対話的で深い学びに向けた授業改善」が促され、大学では高校で身につけた「思考力・判断力・表現力」を前提とした質の高い教育の展開が期待できるとされています。
2つ目の英語の「4技能評価」。これは現行「大学入試センター試験」で実施されている「読む」「聞く」テストに、「書く」「話す」技能の評価を加えようというものです。急速に進むグローバル化へ対応するために、コミュニケーション重視の英語教育が一層求められていることが背景にあるわけですが、この「書く」「話す」テストのノウハウは、民間の検定試験実施会社の開発が相当進んでいるので、それを活用しようというものです。ケンブリッジ英語検定、TOEFL iBT、TOEIC(L&R・S&W)、実用英語技能検定(英検)などが共通テストの「英語」の試験として、成績提供システムに参加することが決定しています。受験生は、高校3年生以降の4月~12月の間に受験した2回までの検定試験の結果を共通テストの成績として、大学に提供することになります。
3つ目の「調査書等の見直し」。これは、「主体性を持って多様な人々と協働して学ぶ態度」を評価するため、高校生一人一人が積み上げてきた大学入学前の教育活動を評価することを目的としています。現行の調査書は、A3見開き1枚の様式となっていますが、この制限を撤廃して、より弾力的に記載できるようにするため、2021年度入試では調査書に記載される内容量がさらに増えるほか、「志願者本人の記載する資料※」の提出が求められる予定です。これは大きく、①活動報告書(「総合的な学習の時間」等において取り組んだ課題研究等、生徒会活動、部活動、ボランティア活動、資格・検定等、各種大会・コンクール等、学校の内外で意欲的に取り組んだ活動など)、②大学入学希望理由書や学習計画書(各大学の学部等の教育内容を踏まえ、入学希望理由や入学後に学びたい内容・計画、大学卒業後を見据えた目標等)からなり、志願者本人が記載するものです。
この大学入学者選抜改革、記述式の導入により、これまで可能だった自己採点ができなくなります。また、50万枚を上回る答案に対してどう採点委員を確保して、採点基準のレベルを合わせるのかも気になります。マスコミも盛んに報じているように、高校、大学双方から批判を含め様々な視点から意見が噴出しているわけですが、レールは敷かれてしまいました。大学全入時代と言われる今でも、大学入試は当事者にとって一生の一大事であり、高校側はその対応が早急に求められています。
御存じのとおり、大学入試センターは「大学入学プレテスト」と称して試行テストを平成29年と30年の2回実施し、思考力・判断力・表現力を問う記述式の問題とは一体どういう問題なのか、そのイメージを明らかにしました。本校の先生方にも問題の分析と、日頃の授業への反映をお願いしたところです。
また、教務部を中心に「主体的・対話的で深い学びに向けた授業改善」の視点を持った研究授業を企画し、思考力・判断力・表現力の育成を目指すとともに、記述式の問題への対応も意識した授業を展開しています。例えば、英語科の授業では、工業科目とも協働し、生徒の発信力を高め、英語を「書く」「話す」活動にアクティブに取り組めるよう、研究・実践を進めています。
さらに、「志願者本人の記載する資料」のうち①活動報告書については、今年度から各行事や学期の終わりごとに生徒たちに記述式の振り返りを求め、ポートフォリオ(学習の過程や成果などの記録を、計画的にファイル等にためておくこと)として記録を残すことを始めたところです。
これらの取組はまだ緒に就いたばかりですが、県内の他の工業系高校とも情報交換を密にしながら、新しい入試制度に向かって用意周到に対応するつもりです。
※「志願者本人の記載する資料」のうち、①活動報告書は、文字通り生徒が活動したことについて記述します。つまり、活動した生徒だけが書けることになります。ボランティアを積極的にしたり、資格試験に意欲的にチャレンジしたりすればするほど充実した報告書が書けるわけです。この報告書が提出できると、入試の際に加点の対象になることが十分に考えられます。また、本校では全員が課題研究に取り組みますが、研究の中心的なリーダーとなって取り組んだ生徒と、先生やリーダーに指示されたことだけに取り組んだ生徒とでは報告書の内容に違いが出てくることは明らかです。高校生活をより主体的に送り、充実させることで報告書の内容も豊かで充実してくることでしょう。
②大学入学希望理由書や学習計画書は、大学に入って自分が何をどのように学びたいのかを詳細に記述します。大学側はこれまで学力で受験生をふるい落としていました。しかし、現在「大学全入時代」と言われるように、大学の定員数と大学進学希望者数に差がありません。受験生はより好みさえしなければどこかの大学には入学できます。そのような中、学ぶ目的意識が乏しい学生が入学後に伸び悩むことを目の当たりにし、苦慮している大学側としては、「入学後も主体的に学んでいく学生を取りたい」という意識に傾くのは当然であり、「大学で学べること」と「生徒が学びたいこと」のマッチングがより重視されるようになっているわけです。
本校では、大学進学だけではなく、就職に関しても、将来どのような仕事をしたいのか、その仕事をするために自分に足りないものは何かを考えさせることにも力を入れています。
【校長】
月やあらぬ

インフルエンザ等での不参加者もなく、197人全員が6時5分、無事出発しました。
保護者の皆さまには早朝からの送迎、大変お世話になりました。事故・怪我なく旅程が進み、楽しい思い出を沢山作ってきてほしいと願っています。

「梅に鶯」連想で、その梅の木にウグイスが来て「ホ~ホケキョ♪」と鳴いている写真を撮ろうと昨日10分ほど待ってみましたが、とうとう来ませんでした。写真部の生徒たちが校内で「一瞬」を狙っている姿を時々目にし、その粘り強さに頭が下がります。私は早々引きあげました。
鳥のことを解説したあるサイトに、「梅の木に止まっている鳥はメジロの可能性が非常に高い。ウグイスとメジロは姿が似ているのと、メジロはウグイスの鳴き声と同じタイミングで梅の木に止まるため、ウグイスと勘違いする人が大変多い・・・」とかありました。私、メジロとウグイスの見分けはつきません。もし写真が撮れていたら、あわや梅の木に止まるメジロの写真を誤ってHPに載せるところだったかもしれません。冷や汗ものです。
梅の花について誰かと話すと、意外なことに桜より梅の花のほうが好きだという人が多いように思います。桜の花の儚さの美しさに対して、梅の花は何かしら力強さを感じます。その香りにも魅せられている私は、今年楽しみにしていることがあります。人吉市大畑(おこば)町の「人吉梅林」を訪ねることです。市のHPによると「白加賀(しらかが)や青軸(あおじく)を中心に、鶯宿(おうしゅく)など白桃系統も合わせた約4,600本の梅の花が咲き誇ります。周辺一帯は梅の香りに包まれ、白やピンク色の花が広大な斜面を彩る優美な世界に・・・」とありました。ずっと前から一度行ってみたい・・・と思っていました。せっかく縁あって人吉で勤務しているのに、昨年は都合で行けなかったので今年こそ。催事も行われる2月24日(日)が待ち遠しいです。できれば、昨年9月に大畑駅に開業したフレンチレストランにも足を運んでみたいです。
最後に・・・、梅ときたら私にとっては「鶯」じゃなくて、「月やあらぬ」が条件反射です。
恋人を失った男が、去年の春にその恋人とともに過ごした、もう住む人のいない家を訪れて詠んだ在原業平のこの和歌、切なすぎます。

あなたと共に見上げたあの月も、あなたと一緒に芳しい梅の香りを楽しんだ春も、そしてあなたまでもお隠れになり、私の周りのものは何もかも変わってしまった気がする。私だけは元とのままで変わらないのに・・・と、世の無常と手が届かない所に行ってしまった恋人に思いを馳せ嘆いている歌だと高校の時に教わりました。
伊勢物語の4段の悲恋をもとにしたラブストーリー、我が家の本立てにもそのコミック本があります。
間もなく別れの季節、3月がやってきます。
【校長】
2019年と国道219号線のワクワクする関係
明けましておめでとうございます。皆様には希望に満ちたいい新年をお迎えになられたことと思います。今年も本校のHPをどうぞ宜しくお願いします。
さて、生徒の皆さん方はお正月、いかがお過ごしでしたか?
球磨川では早くも3日に、寒風を衝いてカヌー部が初こぎをしたと報告を受けました。
私はというと、学校に通う子がいた頃は、元日の朝はそれなりの緊張感があったように記憶しています。でも、みんな巣立ってしまった今、大きな感慨もなくこたつの中で本を読んだり、始業式で何を語りかけようかと考えたり・・・そんな数日間でした。
とはいうものの、これから1年間お世話になる新年号の2019という数字には何かしらワクワク*するものがあります。
既に昨年11月27日の記事でも話題にした通り、2019は3×673と素因数分解され、2つの素数の積として表される「半素数」です。そして、今日を含め残り114日になった平成31年、この31は素数です。
早速、1から9までの数字をこの順に並べて、加減乗除等を施して2019と31を作る小町算をしてみます。
1+2345-6×7×8+9=2019
1×2+345×6-7×8+√9=2019
-1+2+(3!)!!!-45+6×7×8×9=2019
(1×2-3×4+5+678)×√9=2019
{(1+2)!-3}×(4!!-5!!!+678-√9)=2019
12×3+4×5-6×7+8+9=31
12÷3+√4-5+6+7+8+9=31
(1+2+3)×4+56÷7+8-9=31
1×2÷3×4×5×6-7!!!-8!!!!!+√9=31
sin-1(1/2)-tan-1(√3)-4+(5-6)×7+8×9=31
どちらもとりあえず5通りずつできあがりました。まだまだできそうな気がします。
昨年12月19日の記事でも触れたとおり、6[+]4[×]7[-]5=29 程度ではありますが、小町算は就職試験のSPIの常連で筆記試験でも多くの企業が出題しています。日頃からこういう機会を捉えて、紙と鉛筆を持って実際に試行錯誤しておくと、数に関する感覚が磨かれ備えは万全になるはずです。誰も考えつかないという渾身の一式ができあがったら是非教えてください。
暇つぶし?のついでに、今年の素数日も調べてみました。
素数日とは、2019年2月21日を20190221のように8桁で表すと素数になる日です。ネット上の「素数一覧」のサイトから拾い出した今年の素数日は次の19日です。
20190221、20190227、20190301、20190319、20190323
20190421、20190523、20190529、20190601、20190613
20190719、20190811、20190823、20190913、20191009
20191027、20191109、20191117、20191231
和暦(平成31年)ではどうなんだ?と、考えるのは自然なことです。このまま何も起きなければ、1989年1月8日に始まった平成は、11070日続いて、今年の4月30日に終わることになります。31****のような6桁表示の素数日は次のとおりわずか7日でした。
310111、310117、310127、310129、310223、310313
310423
工業高校で学び数字とは縁が切れないはずの皆さん方に、数字を見る目や数的処理のセンスが高まるようにとの願いを込めて、今年もこのサイトを充実していくつもりです。どうぞ宜しくお願いします。
最後に・・・、本原稿は下の注釈まで合わせて全部で2019文字です。
【校長】

ちなみに、八代市から人吉市までの約40kmの間に「国道219」の看板が全部で何箇所立っているか数えたことがあります。全部で27箇所でした。平均して1.4kmに1回、219という数字が嫌が上でも目に飛び込んできます。

先ほども触れたように、2019のほうは、2019=3✕673 でした。
どちらも3という素因数が共通しています。これがワクワクする原因でした。
ワクワクしたついでにちょっとしたクイズを作ってみました。下の①~⑤に当てはまる数字は何でしょう?数学検定3級程度の規則性を見つける問題です。
3✕ 73= 219
3✕173=【 ① 】
3✕273=【 ② 】
3✕373=【 ③ 】
3✕473=【 ④ 】
3✕573=【 ⑤ 】
3✕673= 2019
答 ①:519、②:819、②:1119、③:1419、⑤:1719
※300ずつ増えている理由は?
鹿と3に関連したクイズをもう一つ。漢和辞典で一番画数の多い漢字は何でしょう?
憂鬱(ゆううつ)の鬱ではありません。29画です。答は鹿を上に1つ下に2つ計3つ書いた「麤」で33画です。この漢字は「粗」と同じで、音読みは「ソ」、訓読みは「あらい」と読むようです。ちなみに牛3つの犇は「ひしめく」と読みますが、驫や猋、羴という漢字もあります。何と読むか知ってますか?猫が3つの漢字は見つかりませんでした。
球磨工の情報を発信中!
リンクはこちらから
学校情報
〒868‐8515
熊本県人吉市城本町800番地
TEL 0966-22-4189
FAX 0966-22-5049
E-mail
kuma-th@pref.kumamoto.lg.jp
熊本県教育情報システム
登録機関
管理責任者 校長 坂本道彦
運用担当者 ホームページ係