SSHのページ

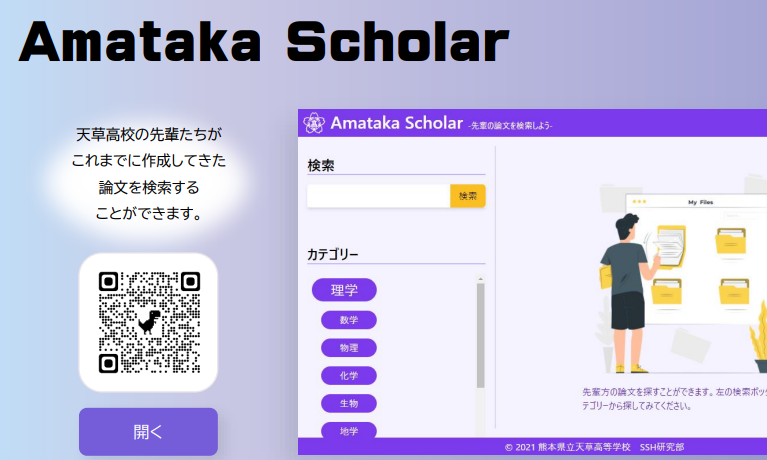
数科学探究Ⅰで2次方程式に関するゲームを行いました

投稿日時 : 2018/05/21  学校サイト管理者 
5月21日(月) 数科学探究Ⅰの第2講義が始まりました。
今回は「2次方程式の有理数解について考察すること」がテーマです。
初めに次の3つのステップで行うゲームをしました。
①先手の生徒が3つの数字を選び後手の生徒に渡します。
②後手の生徒は3つの数字を2次方程式の係数にあてはめて、先手の生徒に返します。
③先手の生徒は、その2次方程式を解き、有理数解であれば勝ちとなります。
つまり、2次方程式の係数に入る数字をどのように入れ替えても有理数解となる3つの数字を後手に渡すことができれば、必ず先手の勝ち（先手必勝）となるのです。
みなさんはどう思いますか。
講義を受けた生徒たちは、自分たちで数字を出し合いゲームをする中で実験を行い、一つの先手必勝パターンを見つけていたようです。
次回は、先手必勝パターンが本当に存在するのかについて考察・検証します。