徒然雑記帖
最後のお給料を素因数分解してみました!
定年を前に、一つ一つの学校行事が感慨深く終わっています。「あと残るは、24日の修了式と27日の退任式か・・・」と、しみじみと感じ入る日が続いていた3月19日(木)、給与支給日でした。虚を突かれました!
いつもなら明細だけを抜き取り、再利用のため事務室に返却する封筒(給与袋)を、担当者から「袋ごと持って帰ってください!」と言われてしまったからです。
「現役最後の最後のお給料!」、実に感慨深いものがありました
給料を毎月毎月きちんと頂けたということは、県職員として忠実に勤務したということは勿論、健康な身体で働けたということであり、実は大変ありがたいことなんですよね。そういう当たり前のことを、現役最後の給与を頂いた日にかみしめました。
ところで、その支給総額、生徒の皆さんたちが情報技術基礎で習った16進数表記で表すと「?FEBD」円(最上位の数は内緒)です。
これまで「自分が毎月もらっているお給料が素数なのか?」とか、一度も考えたことがなかったことに気付き(素数好きの私としては実に不覚でした)、この記念すべき最後の給与総額で「最後の素数判定」をしてみることにしました。
結果は、11×●▲●■◆(2箇所の●は同じ数字)と素因数分解できました。素数ではなかったものの、2つの素数の積ということで「半素数」。一茶の句にある『めでたさも中ぐらいなり』を思い出しながら、これまた感慨深いものがありました。
それにしても、今日も出てきてしまいました。「11」が。
この数字、最近見ることが多くて戸惑っています。たまたま時計を見たら11時11分だったり、目の前を走るクルマのナンバーが11だったり、温度計を見ると11℃だったりと。
日本では古くから言葉は霊的な力があり、魂を持っていると信じられ「言霊(ことだま)」と呼ばれています。そして、数字にも同じようにエネルギーがあって「数霊」と称され、吉凶や運勢、先天的な宿命を占う学問体系が数秘術(学)*として確立されています。何となく怖そうな学問名ですよね。
私、詳しくは知りませんが、数秘学では「11」という数字はマスターナンバーとも言われ、非常に強いエネルギーを持つ特殊な数字の一つとして理解されているようです。でも、3.11の東日本大震災だったり、9.11の米国同時多発テロだったりと、在職中に起こった大事件を思い出したとき、11にはあまりいいイメージがないこともあり、11を頻繁に見かけるのは一体何の予兆だろうと戸惑います。
*数秘術(学):ウィキペディアによると、数秘術の創始者は一般的にピタゴラスの定理で有名なピタゴラスとされているようです。彼は「数秘術の父」として知られており、数千年前のギリシャや中国、エジプトやローマでも数秘術が使われていた事を示す証拠が存在しているんだそうです。当時は、許された者にのみ、口頭でその情報が伝えられていたとあります。
それにしても、11って本当に面白い数字ですよね。2プラス9であれば2が素数であり、3プラス8であれば3が素数。4プラス7と考えれば7が、5プラス6であれば5がというふうに、11を構成するものの半分は素数です。逆に言えば半分は非素数です。しかも1プラス10であれば両方とも素数ではありません!ある素数マニアの方は、「11って独善的で、他の数字に非協力的で、わがままな数」と評されていますが、ある意味当たっていると思います。
話を元に戻します。16進数表記の「?FEBD」と素因数分解の「11×●▲●■◆」から、私の給与総額を推測することを試みるほど暇な生徒さんはまさかいないと思います。私たち県職員の給与は、「熊本県職員の給与に関する条例」に基づき、ガラス張りになっていますので、給料表等はすぐにググることができますから。
最後に・・・、社会人になって最初にもらうお給料というのは、就職試験の面接で「初めての給料は何に使うつもりですか」と、よく訊かれていることからも分かるように、とてもメモリアルなものかもしれません。私は両親をうなぎ屋さんに連れていき、祖母にはバナナを一房買ってあげた覚えがあります。そして、最後のお給料というのも、それはそれなりにセンチメンタルなものと思いました。
そうそう、「最後の素数判定」と書きました。今日を最後に素数について思いを巡らすことを永遠に封印することにします。3年間、「なんちゃって素数談義」にお付き合いくださってありがとうございました。
【校長】
♪いいな いいな人間っていいな・・・
昨日(3月2日)の夕方、車にガソリンを入れて行く途中、交差点で停まった時、前に停まっていた車のナンバーが1717でした。
「”いいな いいな“か・・・、漫画日本昔ばなしの主題歌を口ずさみながら、abab型の整数は、ab×101と分解できるから、これは17×101だよね。17と101のどちらも素数だから、1717は半素数(2つの素数の積で表される数のこと)だな・・・」とかぼっと考えていたらびっくり。
何と向かい合って停まっていた先頭の車のナンバーが1818だったんです。「”いや いや”か・・・、それにしても凄い偶然だな・・・きっとどちらも希望ナンバー制度で取得されたのかな・・・」とか考えながら、ひょっとして1919なんていうナンバーの車が前後にいないかと、思わずバックミラーとか覗き込んでしまいました。
と、そこまではよくある話かもしれません。
本当に驚いたのはそれから6時間位経った夜10時15分過ぎのこと、何気に学校のホームページを開いたら、カウンターが1717152だったんです。
「えっ!?、ということは、あと19、即ち20分位で1717171という数字になるな・・・、夕方の1717のナンバーといい、カウンターの1717171といい、こんな日はめったにないよね・・・」とか思い、その瞬間を写真に収める心づもりをしながら、1717171はどのように分解されるんだろう、ひょっとして素数?とか、考え込んでしまいました。
15分ほど電卓片手に色々な数で割ってみましたが、割り切れる数字が見つかりません。
降参してネット上の素数判定機にかけてみたところ、次のように表示されました。
primeは「素数」、compositeは「合成の」という意味ですから、訳は、「1717171は素数でなくて、合成数です」となります。
「1717171も半素数だったとは、何ということだ!」と絶句していたら、ちょっと時間が過ぎてしまったようです。再度ホームページにアクセスしてみたら、1717173で僅かに通り過ぎてしまっていました。あと2分位前に開けていればと、その瞬間に立ち会えなくて残念でした。それにしても、199で割れるとは、思いつくはずないですよね!
気を取り直していつものように、今日取り上げた1717171について、数字の並びをそのままにして、加減乗除等の記号を入れて、この数字が現れた日にちである3月2日をそのまま並べた32を作ってみます。
(1+7)÷(17+1)×(7+1)=32 → 3月2日
(17+17)(-1+7-1)=32 → 3月2日
(1+7)×√{(1+7)×(17+1)}=32 → 3月2日
とりあえず3つできましたが、まだまだできそうです。
生徒の皆さんだったらどのような式を作りますか?渾身の一式ができたら教えてください。
弥生3月になり、日の光に春を実感します。そのような中で家庭学習の期間が続き、気が滅入っている人がいるかもしれません。気分転換に数字に親しんでみませんか?
【校長】
くま川鉄道の記念日をお祝いしましょう!

何のことか分かりますか?
ヒントです。くま川鉄道は、平成元年(1989年)10月1日運行を開始しました。今日が運行開始何日目になると思いますか。四択です。
①10000 ②11111 ③12345 ④20000
難しいですか?

概算で365×30を計算してみると10950日になります。3月というと、それからさらに5カ月後ですから、150日(30×5)を加えて11100というおおよその数字は出てきます。
②の11111が正解です。

私が思うに、くま川鉄道は日付の数字の並びに人一番敏感な社員さんがいらっしゃるようで、これまで数々の記念切符を発行しておられます。
例えば・・・
平成9年9月9日 → スリーナイン記念乗車券
平成10年10月10日 → 満願成就記念きっぷ

平成12年12月12日 → ワンツー幸福きっぷ
平成13年(2001年)1月1日 → ニューセンチュリーきっぷ
令和1年11月11日 → 伍福切符(右写真)
日付数字の並びの縁起を切符に託して、売り上げに繋げるとは、本当に逞しい商魂を感じます。
ひょっとして、今日3月2日に達成する11111日目を記念したイベントをする計画がないのか、少し前にくま川鉄道の総務部の方に尋ねてみました。
残念ながら「ない」ということでした。
そこで、開業記念日である10月1日の数字をそのまま並べた101、3月2日の数字をそのまま並べた32、それらと11111を関係づけながら、今日の記念日を勝手に(without permission)お祝いしたいと思います。
まず、11111に加減乗除等を施して101を作ってみます。
(sin-11+11)×11=101 → 10月1日
(sin-11+{(1+1+1)!}!!!!-1=101 → 10月1日
同様に、32を作ってみます。
[{(1+1+1+1)!!}!!!!]×1=32 → 3月2日
くま川鉄道は、人吉温泉駅から人吉盆地の東端に所在する湯前駅まで、約24.8kmを結ぶ人吉・球磨地域にはなくてはならない公共交通機関です。平成元年(1989年)から人吉球磨地域の市町村と民間会社の出資による第3セクター方式で運営されていますが、もともとは旧鉄道省・国鉄の湯前線で、1924年(大
その意味で、本当に歴史ある路線で、文化庁の登録有形文化財に駅舎や鉄橋等が19箇所も登録されており、特に湯前駅は、大正13年の開業以来、変わらぬ佇まいを見せています。
湯前駅を話題にしたついでに、このことも。

待合室にピアノが置いてあったのです。前回、11月頃試験勉強を兼ねて各駅を見学して回ったときは、なかったはずです。
音楽を通じて人と人とのつながりを生み出すという願いを込めて、街角などの公共の場所に設置が進んでいるのがストリートピアノです。駅の待合所では、大分県玖珠(くす)町のJR久大線豊後森駅や奈良市のJR桜井線京終(きょうばて)駅の待合室等に置かれていて、時折利用客が弾いていることはYouTubeを見て知っていました。また、JR品川駅構内のピアノが想定よりも多くの客が来て、駅を利用する乗降客の安全確保が担保できないとの理由で、設置からわずか10日余りで撤去されたとニュースで知り、残念に思っていた折、まさかまさか、くま川鉄道の湯前駅にピアノがあるとは!
ピアノ好きの私としては、この光景を見てとても幸せな気分になりました。このピアノの設置の経緯について色々調べていたら、湯前町の広報誌「広報ゆのまえ2月号」に関連記事を見つけました。それによると、湯前駅近くの賑わいをつくろうと、くま川鉄道の許可を得て設置。ピアノはアップライト型で、昭和55年から数年前まで湯前中学校で使用し、保管されていたものだそうです。ピアノの気持ちになれば、再びたくさんの人の手に触れられることを待ち望んでいることでしょう。「湯~とぴあ」の方に電話で尋ねてみたところ、昨年12月末に設置されて以来、結構な人が弾かれているとのこと。列車を待つ間、名もないピアニストが素敵な曲を奏でているのを私も聞いてみたいものです。
くま川鉄道の乗客は、約8割が高校生であり、実際、人吉・球磨地域にある4つの県立高校はいずれも最寄り駅から徒歩10分以内に位置しています。本校生の場合も、昨日卒業した3年生まで含めると全校生徒の約4割に当たる208人が利用しており、安定した鉄道運行が通学に大きな役割を果たしていると思っています。
これから沿線は春爛漫を迎えます。ピンクの桜、黄色の菜の花、薄紫のレンゲソウ・・・列車通学生以外の方もたまにはこの列車に乗って、心地よい揺れに身を任せながら故郷の田園の彩りを楽しんでみませんか。
【校長】
小論文で思い出すあれこれ

振替休日の24日(月)は、人吉市の最高気温が県内で一番高く、19℃で4月中旬並みだったとか報じられました。学校下の村山公園のモクレンが咲き始めていて、とてもいい香りが漂っていました。思わずパシャリ。
話は変わりますが、先々週から先週にかけて生徒たちの頑張りのおかげで、私までその栄誉の場に立ち会うことが続きました。2月13日には3E 園田慧伍君の知事表敬(国体弓道競技少年男子団体で優勝)、14日は3E 尾形幸河君の教育長表敬(電験3種合格)、16日は専攻科の学生諸君が請け負った芦北郡鎌瀬地区の山の神社の落成祝賀会出席。いずれもホームページで詳細が紹介されていたとおりです。
そして、18日は2AA 浦田星奈さんの「第21回高校生小論文コンクール個人部門奨励賞」の表彰式が福岡県から関係者2名が来校のうえ、校長室で執り行われました。
本コンクールを主催する公益財団法人 生涯学習振興財団(本部:福岡県柳川市)のホームページには、高校生小論文コンクール「今こそ大志を語れ!」の募集要項が次のようにあります。
「高校生を対象に、高校教育及び社会教育の見地から、次代を担う青少年の溌剌とした自己形成と、健全な意識形成に寄与することを期待するもので、●自分の未来、●人生の夢や目標、●今熱中していること、●高校生活、●ボランティア活動…のような個人的なこと・関心事から社会的提言にいたるまで、自由に副題をつけて400字詰原稿用紙で1,200字以上1,600字以内で、小論文スタイルで表現してください」
「笑顔で溢れる未来に」と題する浦田さんの作品、改めて読ませていただきました。「大工であるお父様と一緒に将来一緒に家を建てたい」という決意の下、本校建築科に入学したこと、「将来は大学に進学して沢山の人を笑顔にできるような家を設計するとともに、一段落したらその経験を生かして工業高校で教員として、学んだことを次の世代に伝えていきたい」という熱い思いがしたためてありました。文字に綴るという形にすることが、人生を描くエネルギーになると信じます。浦田さん、受賞本当におめでとうございます。
ところで、生徒の皆さんに改めて聞きます。小論文って一体何だと思いますか。「はぁ、何か難しいことが書いてあるやつ?」なんて答えますか。
では、作文とどう違うのでしょう。
私は国語の教師ではありませんので、それについて厳密なことを述べることはようしませんが、「短い論文」である小論文は、「自分の意見を論理的に述べる」ことを目的として読み手を説得する狙いを持って書く文章で、単に経験や体験を元にした自分の主観的な考えを「伝える」ことが目的の作文とは違う・・・、といった説明を(教諭時代、進路指導部で進学係を務めていた頃)していました。今もそうであると信じているわけですが、大きく外れてはいないはずです。
大学進学を考えている人は、小論文が課されることを知って、どう対処しようかと悩んでいる人がいるかもしれません。そのような方は、なぜ大学は採点が簡単なマーク式の問題ではなく、面倒な小論文問題をわざわざ出題しているのか、まずはそこを考えてみることが大事かもしれません。
大学受験の小論文で問われている力は、「与えられた情報を読み取って、自分の意見を論理的に述べる能力」と言い切っていいと思います。これは、大学に入学して、レポートや論文を書く際に非常に重要になる力と重なります。大学は小論文の問題を通して、大学生として必要最低限の力、即ち論理的な文章読解・論述ができる能力を測っているわけです。
既に国語で習ったとおり、小論文は、序論(自分の意見を立場を明確にしながら述べる)→本論(具体例を交えながら自分の意見を裏付けていく)→結論(自分の意見を再度述べる:序論部と同じ表現の繰り返しにならないように注意)で書くことが基本です。このような意見論述能力と論理的文章構成能力は、ひたすら小論文を書いて鍛えるしかないのかもしれません。
当時、私は「日頃から環境問題、少子高齢化、教育経済格差などのトレンドな話題に敏感になり、自分の意見を頭の中でまとめてみるという練習を積み重ねておくことが肝要」と、口癖のように言っていました。例えば、「AIは、人の仕事を奪う」と頻繁に耳にしますが、本当に人の仕事を奪うのか、奪われないためにはどんな力を身に付けておかないといけないのか、そういったことに対して自分の意見を持っておくことが大事だということです。そのためにも、新聞の社説を読むことを勧めていました。他の人の意見を知ることはテーマに対して深く考える機会になるからです。
余談になりますが、私がこれまで出会った小論文のテーマで一番驚いたものを紹介します。2014年(平成26年)に愛知医科大学で出題された「(自分が浮気したから)婚約者に別れの手紙を書いてください」というものです。
「青春を捨て彼女も作らずに今まで一心不乱に勉強した結果をこれで出せというのか!?」と、受験生の間で大きな話題になりましたので、当時中学生だった皆さんたちの耳にもひょっとして入っていたかもしれません。
「あなたにはこれまで3年間真剣なお付き合いをしてきて、来年くらいに結婚の約束をしている彼ないしは彼女がいるとします。ところが2カ月前にふとしたことで知り合った別の人が好きになってしまい、今付き合っている人と別れる決心をしました。600字以内でお別れの手紙を書いてください」
もし、医学部を目指す受験生の立場に立ったとしたら、どのような手紙を書きますか?
「涙を流しながら書いた受験生もいたかも・・・」とか、「恋愛体験がない人には絶対的に不利かなぁ・・・」、私は考えれば考えるほど「一体この小論文は受験生(医師)の資質・能力の何を探ろうとしているんだろう」と悩んでしまいました。
ある予備校の先生の見立てには、「これは記述力だけでなく想像力や人間性まで問われる非常に高度な問題で、病状や余命、医療ミス等に関して、本人や家族に告知する場面が、婚約者に別れを伝えるというという場面に擬せられている」とありました。こうした良くないことを伝える際には、希望を持てるようにすることも大切なのは分かりますが、「君なら素敵な人がきっと見つかるといった言葉を回答に織り込むと評価が上がる可能性が高い・・・」、それ本当かなぁ?
一方、就職試験でも小論文(もどき)を課す企業が少なくありません。進路指導室に保管されていた今年度の受験報告書によると、次のようなテーマで出題されていました。
●入社してから頑張りたいこと、●3年後の自分、●入社後の目標、●将来の夢、●志望職種であなたが発揮できる能力は何か、●〇〇で働く上で一番大切だと思うこと、●あなたが会社に求めること、会社があなたに求めていると思うこと、●あなたにとって仕事とは
「もどき」と敢えて書いたのは、求人票の試験欄に「小論文」を課す旨があるものの、実際に出題されたお題が「あなたはどのような社会人になりたいか」であるなど、明らかに自己PR系であり、これでは書ける内容も主観的なものにならざるをえず、作文だよねと考えられるからです。
ということで、大学進学の小論文と就職の小論文は打つべき対策が違うのかもしれません。
最後に・・・、本校図書館の2月の受入図書に「奇跡の論文図鑑」という本があります。「ラーメンの残り汁でエンジンが動くか」など真面目に論じてあり、論文に込められた底知れない好奇心、愛、情熱、苦悩に驚かされます。
前書きには「人間は万物を研究し、それを論文にしている」とか「研究者はものごとをこんなふうに見ているのか、という目線を味わう!」とかあり、ワクワクします。NHK Eテレ「ろんぶ~ん」を本にしたものです。刺激に満ちた知の世界が広がっており、面白いですよ!
【校長】
紫式部ってやっぱり凄い女性?!
朝からうっすらと雪化粧した大変寒い日、学年末考査の最終日でした。考査が無事に終わり、運動場や体育館からはまた大きな声が戻ってきました。
放課後、校内を回ってみました。


今日は、意を決して、顧問の先生に伺いました。ロボットの動きを制御する各機器とスイッチボックスを繋ぐ多色フラットケーブル(右写真)の色分けのメモなんだそうです。
抵抗のカラーコード*で思い出しました。突然ですが、皆さんは、紫式部と聞いたらどういう反応をするのでしょうか。
「源氏物語」を書いた平安時代の女性、ということを中学校の国語や社会で習ったはずですが、そのことを思い出しますか?
工業に学ぶ皆さん方のことです。紫式部→「むらさきしちぶ」のゴロ合わせが条件反射の「7」と反応するのが普通かもしれません。
紫式部が7って一体何?
ひょっとしたら建築科や建設工学科の皆さんには何のことか分からないかもしれません。ただ、中学校の技術家庭科の電子工作で抵抗のカラーコード*を習っていたら別です。以下に補足しますので、興味があったら読んでください。
抵抗(電気抵抗器)とは、回路に流れる電流値を制限するための電子部品です。電気・電子回路で利用する抵抗には「炭素皮膜抵抗」がよく用いられます。
抵抗は「抵抗器」が正式名称で、回路図などではResistorの頭文字をとって「R」と表される場合が多いです。
抵抗にはさまざま抵抗値があり、テスターでも測定可能ですが、炭素被膜抵抗器には外表面にカラーコード*が着色されていて、抵抗値が一目でわかるようになっています。色に割り当てられた数字は次のとおりです。
黒:0、茶:1、赤:2、橙:3、黄:4、緑:5、青:6、紫:7、灰:8、白:9
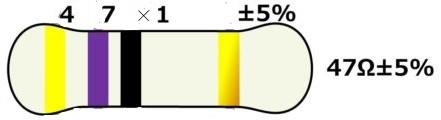
1本目:1桁目(十の位)黄→4
2本目:2桁目(一の位)紫→7
3本目:乗数(10のX乗)黒→0 100=1
4本目:誤差精度(金色:±5%、銀色:±10%)
従って、47×100=47×1=47オーム
ここで各色のゴロあわせによる覚え方は次のとおりです。
黒: 0 黒い礼服
茶: 1 一茶(小林一茶) 「お茶を一杯」という覚え方も
赤: 2 赤いニンジン
橙: 3 第三の男、「だいだい色のみかん」という覚え方も
黄: 4 岸恵子(若い人は知らないかもしれないけど?有名な女優さん)
緑: 5 ミドリゴ (嬰児のこと)
青: 6 青二才のろくでなし
紫: 7 むらさきしちぶ(紫式部)
灰: 8 ハイヤー
白: 9 ホワイトクリスマス
話は大きく変わりますが、紫式部には、ほろ苦い思い出があります。私は、前任校に勤めていたとき世界最古の長編恋愛小説「源氏物語」に魅せられて、かなりのめり込んでいた時期がありました。そして、何を隠そう『勝手に源氏物語検定』と称して、全国の同好の士を相手にネット上の検定を主催しようという壮大な計画を立てて、検定問題(4択)をせっせせっせと作っていました。
作問は全く苦労しません。強引に関係を持つことに長けている主人公の光源氏だけでも、その恋愛嗜好は実にバラエティ豊かです。不倫、略奪愛、ロリコン、男色、熟女愛など何でもありです。しかし、問題を150問位作ったころでしょうか、当然のように行き詰まってしまいました。
古典の文法に関する知識や理解が全然ないので、原文を読んだことは全くありません。漫画をはじめ、色々な作家や予備校の先生たちの現代語訳を読んで得た知識のみが頼りの作問です。原文を読んだことさえない者がそんなことをするのは、やっぱり罰当たり、無謀過ぎると気付いたのです。
それ以来、源氏物語は封印していたわけですが、退職直前になってあることを確かめてみようという思いが湧き上がってきました。
本校のホームページの「校長室より」に3年間でアップしたブログの総文字数と源氏物語の総文字数とではどちらが多いのか確かめたいということです。
当時、入門程度(3級)に次のような問題も作っていたはずです。生徒の皆さんは知っていますか?
Q 源氏物語の総文字数はどのくらいですか。
A ①約200万字 ②約150万字 ③約100万字 ④約50万字
答は、③の約100万文字です。
源氏物語は、一般的には夫藤原宣孝(ふじわら の のぶたか)が没した半年後に書き始められたと言われています。宣孝が亡くなったのが1001年と記録されていますので、源氏物語の執筆開始は1001年~1002年頃になります。完成したのは1008年頃(2008年が源氏物語の源氏物語千年紀に当たるとして、様々な催しものがあり、11月1日が「古典の日」と定められたことを思い出します)とされていますので、7年位で書き上げたことになります。
源氏物語の文字数は、400字詰めの原稿用紙で2,400枚位なので、執筆から完成までの約7年(2,555日)で平均すると、だいたい1日に原稿用紙1枚弱位のペースで書いていた計算になります。あくまで平均です。沢山書いたり、全く書かなったりした日もあったはずです。
では、私の3年間のブログの総文字数はというと、この記事も2,470文字(原稿用紙約6枚)ですから結構な文字数になりそうな気がします。
これまでの全ての記事をワードに張り付けて、ワクワクしながら総合計を電卓で求めてみました。
3年間でこの記事まで含めて全部で157本アップしていることが分かりました。気になる文字数の総合計は・・・
307,197文字(原稿用紙約768枚位)でした。
3年間、自分としても結構書いていたように思いますが、彼女の3分の1にも及ばなかったことを知りました。
別に張り合おうとか、そんなことは思ってもいませんでしたが、「やっぱり紫式部という人は凄い女性だな・・・」、それが今の正直な感想です。
【校長】
祝 総アクセス数1700000件達成
いつも本校のホームページにお越しいただきありがとうございます。
昨日は生憎、雨の日曜日でした。しかし、考査期間中ということもあって学習に十分専念できた人も多かったのではないかと思います。

本校からは陸上部の生徒の皆さんがボランティア(補助員)として運営に携わったはずです。時折強い横なぐりの雨が降る中、大変だったと思います。本当にお疲れ様でした。
右はそのスクリーンショットです。真夜中でも1時間に30件ほどのアクセスをいただいています。ありがたいことです。
それにしても、17日に170万とは、偶然にしてはなかなかいい感じです。昨年11月26日が160万件でしたから、83日間で10万件、一日当たりに直すと約1,205件という計算になります。
170万、無性に素因数分解してみたくなりました。
1700000は17×10万で、17は素数、10万(105)が25×55だから・・・
1700000=17×25×55
従って、その約数は、1, 2, 4, 5, 8, 10, 16, 17, 20, 25, 32, 34, 40, 50, 68, 80, 85, 100, 125, 136, 160, 170, 200, 250, 272, 340, 400, 425, 500, 544, 625, 680, 800, 850, 1000, 1250, 1360, 1700, 2000, 2125, ・・・(途中省略)・・・, 50000, 53125, 68000, 85000, 100000, 106250, 170000, 212500, 340000, 425000, 850000, 1700000
の72個です。
いかがでしょうか?個人的には、170万が160という約数を持つということは感覚的につかみにくい気がしました。しかし、こうして約数を見せられると、17や170、1700が16で割り切れることを予感させて(実際、17÷16=1.0625)、面白いです。
それでは、いつものように1700000の数字の並びをそのままにして、加減乗除等の記号を入れて217(今日の日にち2月17日)を作る小町算ごときで遊んでみます。
(|1-7|)(0!+0!+0!)+0!+0=217 → 2月17日
170+{(0!+0!+0!) ! }!!-0!=217→ 2月17日
17(0!+0!)-[{(0!+0!+0!) ! }!!!]!!!!!!!!!!!!!!=217 → 2月17日
「0!=1」という定義を使って、たちまち3つほど立式できました。
この中でも一番お気に入りは、最初の式です。217を216+1と分けて、216が6番目の立法数(63=216)であることに着目してみました。
生徒の皆さんだったらどのような式を作りましたか?「これは・・・!」という傑作ができたら教えてください。
最後に、170万という数字を見て、考えたり閃いたりすることです。
17だったら聖徳太子の「17条の憲法」などが思い浮かびますが、170万です。残念なことに私は何も思い浮かびません。ネットを検索してみても、商品の型番などに割り当てられている数字以外では、東京都豊島区の郵便番号が〒170-0000とか、某食品メーカーが昨年11月に微生物が検出されたとして、ペットボトル飲料水約170万本を自主回収すると発表したことなどがひっかかってくるだけでした。
ネタがないので、最近私が頭をすご~く悩ました数字の並びに関するクイズを1問ご紹介します。
兵庫県にある私立灘(なだ)中学校の今年の算数の入試問題です。

小学生の柔らかい脳だったらすぐ解けるのかもしれませんが、私は悪戦苦闘しました。少なくとも制限時間を問題数で割った10分位では解けませんでした。
皆さんはいかがでしょうか。ぜひ考えてみてください。
灘中学校の算数入試は、これは算数オリンピックの問題?と見まごうほど数学愛に溢れていて、解いていてワクワクしたり、面白いと感じたりする問題が多く、算数マニアの間ではつとに有名です。この学校の数学の先生たちは、きっと数学が好きなだけでなく、常に問題を考え続け、解く人のことを一生懸命に考えられている探究心が旺盛な方ばかりなのではないかなと、勝手に想像しています。
↓(正解は・・・)
↓
↓
↓
↓
答えは446001です。
でも、ネット上に置かれていたこの問題が本物の入試問題の写し(pdf)としたら、問題文がどうも変なので(「・・・その数の左上にある数の和になっています。」の箇所、正しくは「その数の左上と右上にある数の和になっています。」であるべきです)、ひょっとしたら、問題文の誤りということで全員正解扱いになったかもしれません。
多くの有名予備校や塾がネット上で正解例を発表していますが、どれもこの問題が使われているので、実際の問題と思われます。しかし、試験の前に板書等でその旨の訂正があっていたら話は別です。
【校長】
「勝手にくま鉄検定」上級用新作問題 に挑戦しませんか?
「勝手にくま鉄検定」上級用新作問題 に挑戦してみませんか?
昨年(令和元年)9月8日に実施された「くま鉄検定」で中級に合格した方を対象に、2月2日に上級の試験が行われます。私も学生時代以来久々に一夜漬けを楽しんでいます。そこで、自身の勉強も兼ねて四択方式(実際の試験形式は〇×方式か?)の予想問題を25問(1問4点で100点満点)作問してみました。
くま川鉄道を日々の通学の足にしている生徒の皆さん、何問解けますか。
上級受験予定の方も時間に余裕があるようでしたら、お付き合いください。
【令和2年1月29日】
牛乳1リットルが955mlの話題を巡って

インフルエンザ等で2名が不参加と連絡を受けましたが、出発式を済ませて6時前に鹿児島空港に向けて元気に出発しました。
旅行団を見送り、校長室でネットニュースを見ていたら、「1リットル牛乳は実は1リットルない?」というタイトルが目にとまりました。
何でも小学校の算数授業がきっかけで物議を醸しだしているそうで、「牛乳パックに1000mlと書いてあるのに計算すると955mlしか入っていない!」とありました。
「それって、20年前に生徒に計算させていたことだよね!」と思いながら読み進めてみると、概略次のようなことが書いてありました。
きっかけとなった算数の問題
ある小学校の先生が算数の授業で子どもたちに出した問題:「牛乳パックに入っている牛乳の量は?」というものだっだ。

縦と横の長さは7センチで、高さは19.5センチだ。これをもとに3つの辺を掛けて入る牛乳の量を計算すると…
7×7×19.5=955.5 (立方センチ)
つまり955mlしか入らないというのだ。では差の45mlはどこに入っている?
勿論、上の三角の部分には入っていません!
この謎について、日本乳牛協会が説明をしている。
それは、「牛乳をパックに入れると中に圧力がかかり、膨らむ。そのため、パックは955mlでも、膨らみの分だけ量が増え、1リットル入る」というのだ。
その記事の中で、最後に教育評論家の方が次のような趣旨のことを述べておられますが、本当にそう思います。
「授業の中で身近なものを題材にして勉強するのはとても良いことだと思う。教科書的な解答と現実は違う。もし子どもたちがそういうことを学ぶきっかけになったら素晴らしいと思う・・・」
話は変わりますが、普段何気なく「1,500cc」、「3.5L」などと車のことを呼んでいると思います。生徒の皆さんは、エンジンの排気量とはそもそも何なのか、計算方法はどうなっているのかご存知でしょうか?
私、40代のとき、カワサキ・ZX-10(ゼットエックス-テン)というリッターバイクに2年間ほど乗っていました。丁度その頃、授業では原動機を教えていて、総排気量や圧縮比を学習する単元で生徒に具体的なイメージを持ってもらおうと、そのバイクのエンジンの諸元を板書して総排気量等を計算させたことがあります。
冒頭、「20年前に生徒に計算させていた」と書きましたが、いきなりエンジンの排気量を求めるのではなく、小学校の算数で学んだ「体積」の復習をイントロとして扱い、そこで牛乳パックの容積を求めさせていたのです。
そのとき、45mlの謎についても生徒に考えさせていました。だから、余計に懐かしく今朝の記事を読んだわけです。
ZX-10のカタログ諸元は次のとおりです。
水冷4ストロークDOHC並列4気筒16バルブ
内径×行程 / 圧縮比 74.0mm× 58.0mm / 11.0
これを元に、排気量を計算します。まず、排気量の定義から説明していました。
排気量とはマフラーから出る排気ガスの量ではありません。エンジンの排気量とは、シリンダーの容積を表しています。もっと正確に言うと、エンジンのシリンダー内でピストンが動く範囲(上死点と下死点の間)の体積を行程容積といい、この値とシリンダー(気筒)数との積が総排気量になります。
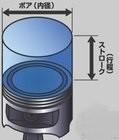
D=πd2SN / 4000
で求めることができます。πを3.14として計算すると、
D= 3.14 × 74.02 × 58.0 × 4 / 4000 ≒ 997.29 cc
ここで、1リットル=1000ccですから、計算上でも確かに約1リットルで、「リッターバイク」と呼ばれることを納得できます。言うまでもありませんが、「ナナハン」と呼ばれるバイクは、この総排気量が750ccということです。
勿論、赤色の公式も、底面積に相当する円の面積を求めるところから説明しますし、4000(=4×1000)に含まれる単位換算の考え方、1cc=1ml=1cm3 など押さえておかなければならないことは盛りだくさんあります。
このようにして排気量を求めた後、車の排気量が多いということはどういうことか、メリットやデメリットを考えさせるのが常でした。
メリットは、エンジンのパワー(動力)が大きくなるので、加速がスムーズになり、上り坂もすいすい登り、最高速度も速くなります。また、振動や音が小さくなることが多いです。
でもデメリットとして、燃費(燃料1L当たりどれだけの距離を走れるか)が悪くなり、重たくなる分頑丈に作らなければならないので必然的に車体価格が高くなることがほとんどです。また、排気量が多いと自動車税も高くなります。
今、若者の車離れがしきりに言われています。私が初任の頃は、機械科の教室には、後ろのロッカーの上などに回し読みされたバイクや車の雑誌が置いてあるのが普通でした。昨今、放課後の教室を回ってもそんな光景は見ません。教壇を離れて15年が経ってしまい、今の生徒たちが車を選ぶ基準もよく分からなくなりました。若い人は今でもやはりデザインなどを重視しているんでしょうか?
いざ運転するというときには、排気量の違いで運転の快適さなどが違ってきます。今は排気量660ccの軽自動車でも結構快適ですが、やはり高速道路ではストレスが募るような気がします。
そう言えば・・・、私が中学生の頃はスバル360のように、排気量がそのまま車名となる例などがありました。その車に乗っていた先生(故人)のお顔を思い出したところです。
これから自動車を購入する3年生の皆さん、ここで述べたようなことも参考にして車選びをしてはいかがでしょうか。
【校長】
60を3進法で表すと?
そうです。待ちに待った2020(ニーゼロニーゼロ)です。
ということで、明けましておめでとうございます。皆様には希望に満ちたいい新年をお迎えになられたことと思います。今年も本校のホームページをどうぞ宜しくお願いします。
生徒の皆さん方はお正月、いかがお過ごしでしたか?
私はというと、昨年9月に生まれて最近よく笑うようになった孫をあやしながら、これから1年間お世話になる新年号の2020という数字についてあれこれと考えていました。
いつもの癖で、とりあえず素因数分解をしました。
abab型の4桁の数は、ab×101ですからabを素因数分解すれば事足ります。パパっと暗算で・・・
2020=22×5×101
従って、その約数は1, 2, 4, 5, 10, 20, 101, 202, 404, 505, 1010, 2020の12個です。
早速、1から9までの数字を順に並べて、加減乗除等を施して2020と2(令和2年)を作る小町算(ごとき)をしてみました。
12÷3+4×567×8÷9=2020
12÷3-4×56÷(7-8)×9=2020
(123+4)×(5+6)+7×89=2020
(√(123×4-56×7)+8)÷9=2
12÷3×4+5!!-6×7+8!!!!!!-√9=2
sin-1(1/2)-tan-1(√3)+4×5+6!!!-7+|8-9|=2
どちらもとりあえず3通りずつできあがりました。まだまだいくらでも作れそうな気がします。中でも一番のお気に入りは最初の式です。括弧も階乗も何もなくて実にシンプルです。
次に、いつものように総アクセス数に着目して遊んでみました。
紅白を見た後、短い眠りに落ちて目覚めたとき、すなわち2020年1月1日午前5時51分現在のアクセス数は1641554でした。
今年のアクセスの状況を分析する際に基準となるこの記念すべき数字の並びをそのままにして、2020と2を作りました。
1-6!!+415×5-4!!=2020
16÷4+1+5÷5-4=2
どちらも意外にあっさりとできました。
もし、誰も考えつかないという渾身の一式ができあがったら是非教えてください。
8【+】6【×】4【-】2=30 程度ですが、小町算は就職試験のSPIの常連で筆記試験でも多くの企業が出題しています。日頃からこういう機会を捉えて、紙と鉛筆を持って実際に試行錯誤しておくと数に関する感覚が磨かれ備えは万全になるはずです。

こたつ布団の絵柄といい、ネズミやイノシシが着ている羽織りの絵柄といい、とても絶妙なタッチで描いてあり大変癒されます。
私、2019年から2020年にバトンを渡すこのイラスト見ながら高校3年の時の数学の授業の一コマを思い出しました。
突然ですが 20192020 と 20202019 はどちらが大きいと思いますか?
実は・・・、3学期の最初の授業で、先生(故人)が黒板にいきなり
「19771978 と 19781977 はどちらが大きいか」
と板書されました。私が高校3年のときの新年は1977年(昭和52年)から1978年に変わった年で、それをもとにした問題でした。
私、次のように考えたと記憶しています。
12(=1)<21(=2)
23(=8)<32(=9)
・・・(これから類推して)・・・
19771978 <19781977 ではないか?
「ハイ!」と手を挙げて発表しなかったからよかったです。そんなに甘くはありませんでした。なぜなら、次から大小関係が逆転するからです。
34(=81)>43(=64)
45(=1024)>54(=625)
一体どうなっているんでしょう?
昨年の始業式で毎日少しでも(0.01でも)気持ちを+(プラス)に持ち続けることの大切さを説明した際に、
0.99365≒0.03 1365=1 1.01365≒37.8
の話をしました。指数関数の怖さを実感する数式だったわけですが、果たして20192020 と 20202019 のどちらが大きいか、直感で分かりますか?
手元に電卓がある人はキーを叩いてみてください。機種によっては計算結果を表示することが可能な範囲を超えているということで、エラーになるかもしれませんが・・・。
答は敢えて明かしません。数学的に厳密な議論をしようとすると、y=logx/x の曲線の形を考える(数学Ⅲの範囲)ことになりやっかいです。でも、興味がある人はぜひ考えてみてください。将来、仕事の道具にlogを使っている人が必ずいるはずです。
工業高校で学び数字とは縁が切れないはずの皆さん方に、数字を見る目や数的処理のセンスが高まるようにとの願いを込めて、今年もこのサイトを充実させていくつもりです。どうぞ宜しくお願いします。
最後に・・・、本原稿は全部で2020文字です。
【校長】
祝 総アクセス数1600000件達成
いつも本校のホームページにお越しいただきありがとうございます。

学校は本日26日(火)から期末考査に入り、学校全体が日頃に比べて静かな雰囲気に包まれています。写真は夜9時過ぎに、人吉高校との合同寮「凛然寮」にお邪魔した際に撮った黙学に励む寮生の様子です。
高校の定期考査といえば・・・、私の頃は「政治経済」で時事問題が必ず数問出題されていて、友達同士で何が出るか当てっこしていた思い出があります。
本校の試験で時事問題が出題されるとしたら2年生で学ぶ「現代社会」かな?と思い、教科担当の先生に尋ねてみました。期待に反し、授業で教えた範囲からだけで時事問題の出題はしてないそうです。
「就職試験でも時事問題は頻繁に出ていますし、新聞を読む習慣を付けさせるためにも私が現社の教科担当者なら多分出題するよね・・・」と思いながら、2学期の期間中に起こった社会事象の中から自分だったらどんなことを出題するか考えてみました。絞りに絞って候補に残ったのは次の5つです。
①【 ① 】首相の在任期間が憲政史上で最長を記録
②ラグビーワールドカップ日本大会で【 ② 】が優勝
③東京オリンピックのマラソンと競歩が【 ③ 】で開催することに決定
④世界遺産の【 ④ 】で火災
⑤消費税が10%になり、【 ⑤ 】税率が導入
答と解説 ①安倍、②南アフリカ、③札幌、④首里城、⑤軽減
①11月20日、安倍晋三総理大臣の在職期間が、通算で2887日となり、憲政史上で最長を達成(企業の人事担当者から「安倍」を漢字で正しく書けない高校生が多かったと聞いたことがあります)
②11月2日、ラグビーワールドカップの日本大会決勝が横浜国際総合競技場で行われ、南アフリカがイングランドを32-12で下し、3大会ぶり3度目の優勝を達成
③11月1日、2020年の東京オリンピックのマラソンと競歩は、北海道の札幌で実施することが国際オリンピック委員会調整委員会で正式に決定
④10月31日、沖縄県那覇市の世界遺産にも登録されていた首里城で火災が発生し、正殿など7つの建物が焼失
⑤10月1日、消費税が8%から10%になったことにあわせて、政府は軽減税率を導入する一方、スマホなどによる決済でポイント還元をするなど市場のキャッシュレス化を推進
生徒の皆さんが出題者の立場に立ったとしたら何を出題しますか?
「リチウムイオン電池」の開発に大きく貢献した【 ⑥ 】氏が10月9日にノーベル化学賞に選ばれたことや、10月14日「体育の日」がこの名称の最後の日になったこと(2018年に公布された「国民の祝日に関する法律の一部を改正する法律」により2020年から「体育の日」が「【 ⑦ 】の日」に変わる)を出題ネタにする人がいたかもしれません。(答:⑥吉野彰、⑦スポーツ)
こうして、改めて思い出してみると、色々と心動かされる出来事やショッキングな事件に満ちた2学期だったと実感します。
ところで、今日11月26日午後5時17分、ホームページの総アクセス数がついに1600000件に達しました。
160万、なかなかいい数字です。無性に素因数分解してみたくなりました。
1600000は、16×10万で、16が24、10万(105)が25×55だから、パパっと暗算で・・・
1600000=29×55
従って、その約数は、1, 2, 4, 5, 8, 10, 16, 20, 25, 32, 40, 50, 64, 80, 100, 125, 128, 160, 200, 250, 256, 320, 400, 500, 512, 625, 640, 800, 1000, 1250, 1280, 1600, 2000, 2500, 2560, 3125, 3200, 4000, 5000, 6250, 6400, 8000, 10000, 12500, 12800, 16000, 20000, 25000, 32000, 40000, 50000, 64000, 80000, 100000, 160000, 200000, 320000, 400000, 800000, 1600000
の60個です。
それでは、いつものように1600000の数字の並びをそのままにして、加減乗除等の記号を入れて1126(今日の日にち11月26日:いい風呂)を作る小町算ごときで遊んでみます。
16!!!!!+[{(0!+0!+0!) ! }!!!]!!!!!!!!!!!!!!!-0!-0!=1126→11月26日
このこと、毎回触れていますが「0!=1」というのは定義です。無から有を生み出す関数としてこういう時こそ重宝します!
実を言うと、このところ1日当たり平均して1000件前後のアクセスが続いていたので、160万件達成は12月4日頃かな、と勝手に予想を立てていました。1600000の数字の並びで124を作るのは至って簡単で、「121から128までだったら、何でもかかってこい」と鷹揚に構えていました。
ところが、11月25日から26日かけて、普段の4倍近い3900件余りのアクセスがあり、26日も午後5時までのわずか9時間で3000件近くのアクセスを頂き、予想より8日も早まってしまいました。本当にアクセスが集中しているのなら嬉しい悲鳴ですが、カウンタ回路やそのプログラムが異常をきたして暴走していることも考えられ、怪しさや不気味さを感じます。
いずれにせよ、3桁の124ではなく4桁の1126を作らないといけなくなり、少々慌てました。結局、「!!!!!!!!!!!!!!」なんていう”おばけ”みたいな関数を使わないと私は立式できなかったわけですが、生徒の皆さんだったらどのような式を作りましたか?
最後に、160万という数字を見て、考えたり閃いたりすることです。残念なことに私は何も思い浮かびません。ネットを検索してみても、特に興味を引くようなものを見つけることはできませんでした。唯一あったのは・・・
日本の剣士の数です。次のような英文を見つけました。
There are currently an estimated 1.6 million kendo practitioners in Japan.
日本の剣道の愛好家は、現在およそ160万人と言われています。
160万って、one million (and) six hundred thousandだけでなく、簡単に1.6 millionでも勿論いいわけですが、日本語では160万というように「160×1万」で表記しますが、英語では、「1.6×100万」というように発想するのが面白いと思いました。
【校長】
令和1年11月11日と伍福切符
いつも本校のHPにお越しいただきありがとうございます。
昨年7月17日に総アクセス件数が111111になった日に「レピュニット」について話題にしました。「レピュニット」というのは、111や11111のように1がいくつも並んだ数字のこと(repunit【repeated unitの略】)でした。
そして今日令和1年11月11日も11111のように1が5つ並ぶ記念すべき日です。言うまでもなく、“1”は正の数の始まりの数です。この数字には面白くて不思議な性質があり、その幾つかを昨年7月17日に紹介したところです。
そんなことを思い出していたら、1が沢山続く今日の日に着目している鉄道会社があることを知りました。皆さんがいつもお世話になっているくま川鉄道です。会社のホームページに次のような記載がありました。引用します。
令和1年11月11日(1が5並び)記念の伍福切符販売について
日頃より、弊社運営につきまして、ご高配を賜り厚くお礼申し上げます。
さて、弊社では新しい年号“令和”が始まり、初めての数字並びの記念日に合わせて、おかどめ幸福切符の台紙付き記念切符を発売いたします。
令和1年11月11日は、1が5つ並びますが、算命学によると幸福には5つの種類に分かれ、福寿禄官印という考え方があります。
「福」・・・心の幸福、主に家族から得られる安らぎ感
「寿」・・・美・健康の幸福
「禄」・・・財・お金の幸福
「官」・・・仕事・名誉などの幸福
「印」・・・知識による幸福
この考え方から、この切符を持つ人、または幸せになってもらいたい方に贈る切符として「伍福切符」と名付けました。
発売日 令和元年11月11日(月) 10時より販売開始
販売価格 1枚240円(幸福行切符、専用台紙付き)
販売箇所 人吉温泉駅、くまたび、あさぎり駅、おかどめ幸福駅売店
ネット販売 各箇所10時より販売開始、その後は各署の営業時間に準じます。

“1”が連続する数字が持つ面白い性質に話を戻します。
今日、令和1年11月11日午前11時11分は、111111111のように1が9個連続します。
生徒の皆さん、1111111112の値はいくらになると思いますか?
言い換えれば、111111111×111111111の値です。
ヒントです。手元の電卓を使って次の計算をしてみます。
112=11×11=121
1112=111×111=12321
11112=1111×1111=1234321
111112=11111×11111=123454321
例えば、最後の111112の様子を見ると、答えの最も大きな桁は1から始まり、123・・・と増えていきます。5まで増えると、その後は43・・・と減っていき最後は1で終わっています。
このように、1が連続する数同士の掛け算の答えは、その桁数まで増加して、その後1まで減少し、左右対称の連続した数字が現れるようです。
ということで、1が9つ連続した9桁の数同士の掛け算です。これはどうなるでしょうか?
答えは、
111111111×111111111=12345678987654321
という17桁の数字になります。まぁ、当たり前といえば当たり前ですが、規則正しい数字の並びを見ていると、何やら神秘的なものを感じてしまいます。あなたは知っていましたか? 余裕がある人は、1が10個連続した10桁の数同士の掛け算や11個連続した11桁同士の掛け算がどうなるか考えてみるのも面白いと思います。
最後に・・・、午前11時11分現在の総アクセス数は1579561件でした。ということで、いつものように1579561の数字の並びをそのままにして、加減乗除等の記号を入れて、今日の日にち11月11日をそのまま並べた1111を作ってみることにします。
[{(1+5)!!!-7}×(95+6)]×1=1111 → 11月11日
1111を素因数分解すると11×101になり、そこに着目してみました。あなただったら、どのような式を作りますか?
【校長】
「筒井筒」の研究授業
国語の研究授業を参観しました。教材は伊勢物語の「筒井筒」です。
私は「好きな歴史上の人物を一人挙げよと言われたら、在原業平(ありわらのなりひら)を第一候補にするかな・・・」というほどの業平ファンです。ということで、伊勢物語やそのモデルされる在原業平については、この徒然雑記帳でも以下のとおり4回に渡って取りあげてきました。
平成29年4月18日:「565656」(伊勢物語は56歳で亡くなったとされる在原業平がモデルとされ、第56代清和天皇の御代(みよ)の出来事・・・)、同4月30日:「いずれがあやめかかきつばた」、同5月28日:「業平忌」、平成31年1月15日:「月やあらん」
「業平忌」でも書いていたことですが、和歌に優れ六歌仙の一人でもある業平は、今から約1,200年前に生きた天皇の血を引く由緒正しい実在の貴族です。既存の風習にとらわれず、56年の生涯の中で多くの女性(一説には3,733人)と関係を持っていきます。一夫多妻制の当時の結婚形態を考慮に入れてもスゴイの一言ですが、別にそういう所に憧れるのではなく、反骨の精神で自由奔放にそして風流に生きたその生き様に心惹かれるわけです。
伊勢物語、手元のシラバスによると、本校では2年生の国語総合で2学期に学習するようです。機会があれば、ぜひ参観してみたいと3年間ずっと思っていて、とうとう実現しました。それも研究授業という形で。内容は第23段、「筒井筒(つついづつ、旧かなでは「つつゐづつ」)です。筒井筒とは、今では見かけなくなりましたが、丸く掘った井戸の枠のことで、互いに惹かれていた幼馴染の男女が結婚し、その後が波乱万丈という物語です。
事前に配られた学習指導案では、「ホットシーティングを行うことで、登場人物の言動や心情について読みを深める」とあります。ホットシーティングとは、恥ずかしながら初めて目にする教育用語でした。一体どんな授業だろうとワクワクして建築2年の教室に向かいました。
目の前で展開された授業は、生徒が登場人物になりきり、他の生徒からの質問(インタビュー)に応えるというもので、「なるほどこういう活動をしたら、感情移入をしながら自分のこととして文学を読む力がつくのだな・・・」と実感しました。
この物語、幼馴染が結婚したところまではよかったのですが、妻の親が亡くなり経済的な援助が受けられないと分かると、途端に別の女をこしらえ、しかも女が浮気をしているのではないかと疑い始めて庭に隠れて様子を窺うなど、男の身勝手さが光って?います。千年も前からホントに男ってヤツは・・・と感じている女子の皆さんも多かったはずです。ということで、男女の機微を察するには十分過ぎるこの教材、生徒たちのインタビューとその回答も迫真に迫ったものがあり、大変面白かったです。
話は変わりますが、生徒の皆さん、一週間前の11月1日は何の日だったか知っていますか?
答えは「古典の日」です。源氏物語千年紀を記念して11年前の平成20年(2008年)11月1日に京都で宣言されました。その2年後の平成22年、国の法律でも制定されています。古典は文法が難しく、私自身は高校のときアトピーが出るほど毛嫌いしていた悲しい思い出があります。でも、「現代語訳を読むとしみじみ読める作品って意外に多いよね」というのが今の実感で、その代表作が伊勢物語と思っています。
伊勢物語は全部で125段ですから、薄い文庫本1冊程度です。一話一話も短く、簡潔です。どこから読んでもいいし、読み飛ばしてもいいので疲れません。その意味で古典に親しむ入口として最適です。それでいて、深い内容があり、とても面白いです。何が、面白いのか?何と言っても、歌がいいです。現代人と変わらぬ喜怒哀楽を詠んでいますので、「この気持ち、わかるなぁ」と共感できる歌が必ず見つかるはずです。詠まれている歌は、男女の恋愛、男同士の友情、親子の情愛、年を取ること、愛する人の死、旅の情緒など実に多彩です。生徒の皆さんもこれをきっかけに伊勢物語を読んでみませんか?
その取り掛かりとしてお薦めは、詩人の俵万智さんの「恋する伊勢物語」(ちくま文庫)です。伊勢物語を現代語訳しながら、個人的恋愛論や体験談を交えながらその面白さを伝えるユーモラスなエッセイです。残念なことに本校の図書館にはないそうです。
【校長】
放課後の風景
いつも本校のホームページにお越しいただきありがとうございます。
長らく記事をアップしていませんでした。8月25日以来72日ぶりです。「勝手にくま鉄検定」のほうに少々力を入れ過ぎていたかもしれません。
ところで、今日は11月5日。数字をそのまま並べたら115です。
そして、たまたま開いたホームページの夕方4時42分現在の総アクセス数は、1574695件でした。一桁目が5ですから閃きました。
ひょっとして115の倍数になっていないかな・・・?と。
早速割り算したら、1574625÷115=13693 割り切れました!
偶然かもしれませんが、思ったことが当たって嬉しくなりました。きっとエンドルフィン(脳内麻薬)が出たのかもしれません。久々に放課後の教室の様子を見回ってみようという気持ちが高まりました。
「秋の日はつるべ落とし」で、あっという間に日が暮れるわけですが、生徒の皆さんたちが蛍光灯の明かりの下でしていたこととは・・・?
校内6箇所でパシャリ。
上段左:11月13日に行われる生徒研究発表会の練習中の建築科3年生。エンディングを工夫していました。どう仕上がるのか楽しみです。
上段右:11月10日実施予定の2級建築施工管理技術検定試験に向けて、過去問を解いている建築科3年生14名。
中段左:11月8日実施予定の日本漢字能力検定(漢検)の2級・準2級に向けて学習中。2級受験予定の生徒は四字熟語を覚えていました。ちらっと見えましたが、哀毀骨立(あいきこつりつ)、一筆勾消(いっぴつこうしょう)・・・本当に難しいです!!
中段右:12月7日実施予定の第1種電気工事士(技能試験)に向けて練習中の電気科2年生。単線図を複線図に直して・・・、電工ナイフでケガをしないように注意してください。
下段左:建築科製図室で建築科1年生が4人残って「破線」など各種の線を何本も引いていました。建築製図の事情は知りませんが、機械製図では、太い実線、細い実線、細い破線、細い一点鎖線、細い二点鎖線の5種類があります。これらをきちんと引けることは製図のイロハです。でも、この基本的な練習が意外におろそかにされがちでもあります。太い線も細い線も「濃く」描くことが大事です。
下段右:機械科2年生の生徒が、機械科の製図室に1人残って(剣道部のお友達の付き添いあり)「軸受け」の図面を引いていました。
黙々と図面を引いている姿、工業高校らしくて一番好きな光景です。
生徒たち、それぞれ今やるべきことを頑張っていました。
【校長】
祝 総アクセス数1500000件達成
いつも本校のHPにお越しいただきありがとうございます。
日曜日の今日、秋雨前線が九州付近に停滞しているとかで、昼前から雨模様になってしまいました。夏休みも残り1週間になり、思い出作りの旅行とか計画していた皆さんにとっては残念だったかもしれません。今週は明日以降も曇りや雨の日が多い見込みなんだそうです。
ところで、私は夢の中でしたが、今朝午前3時半前後にHPの総アクセス数が1500000件に届いたはずです。
150万、なかなかいい数字です。無性に素因数分解してみたくなりました。
1500000は、15×10万で、15が3×5、10万(105)が25×55だから、パパっと暗算で・・・
1500000=25×3×56
従って、その約数は、1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 25, 30, 32, 40, 48, 50, 60, 75, 80, 96, 100, 120, 125, 150, 160, 200, 240, 250, 300, 375, 400, 480, 500, 600, 625, 750, 800, 1000, 1200, 1250, 1500, 1875, 2000, 2400, 2500, 3000, 3125, 3750, 4000, 5000, 6000, 6250, 7500, 9375, 10000, 12000,・・・(途中略)・・・,100000, 125000, 150000, 187500, 250000, 300000, 375000, 500000, 750000, 1500000
の84個です。
それでは、いつものように1500000の数字の並びをそのままにして、加減乗除等の記号を入れて825(今日の日にち8月25日)を作ってみることにします。なかなか手強かったですが、暫く色々とやっていたらできました。
{(|1-5|)!!}!!!!+cos0+0+
[{(0!+0!+0!)!}!!!]!!!!!!!=825→8月25日
「0!=1」というのは定義ですが、cos0=1と同様、無から有を生み出す関数としてこういう時に使えますよね!
ところで、生徒の皆さんは150万という数字を見て、何か考えたり閃いたりすることはありますか?
以前、130万が達成されたとき、「130万の壁」について記載しました。それとも関連しますが、昨年(2018年)1月に大きな税制改革があり、パート勤務の人たちの配偶者控除に関して「150万の壁」というのができました。だから、ネット上で「150万」を検索するとこの「150万の壁」ばかりがやたらにずら~っと出てきます。この「配偶者控除」、長年夫婦をやっているとよく聞く言葉かもしれませんが、生徒の皆さんにとっては、あまりなじみがないかもしれません。ということで、今日ここで深入りすることはやめておきます。
冒頭に、「私は夢の中でした・・・」と書きました。この「夢」で思い出したことがありますので、そのことを紹介します。
先月、外国人労働者を扱ったとても考えさせられるNHKスペシャルを見ました。そのタイトル、何と「夢」と「150万」がキーワードでした。早々、図書館に保管されていた当日の新聞を見つけて、テレビ欄から正確な番組名を確認しました。
「夢をつかみにきたけれど ルポ・外国人労働者150万人時代」
日本には今、150万人もの外国人労働者がいるわけですが、そのほとんどが単純労働に従事しています。異国の地、ニッポンで非業の死を遂げた外国人労働者のリアルな現実から、現在の日本社会のゆがみを浮き彫りにするとても考えさせられる番組でした。これからの我が国で活躍が期待される生徒の皆さんこそ見てほしいと思いながら視聴したところです。この番組見ましたか? YouTubeにも置いてあるようですよ。
【校長】
「勝手にくま鉄検定」(第1セット目)です!
くま川鉄道は、今年で30周年を迎えるに当たり、9月8日(日)に「令和元年くま鉄検定」を行うと、新聞等で報じられました。かつて雨後の筍のようにご当地検定があちこちで開催されていましたが、ほとんどが受験生不足に泣かされ休止に追い込まれている中、鉄道関係の検定を敢えて行うという英断に心から拍手を送りたいと思います。鉄ちゃんを自認する筆者は、かつてJR九州が「九州鉄道検定」を行っていたことを思い出しましたが、鉄道大好きの皆さん、ワクワクしませんか?
私、迷わず申し込んで受験をしてきました。多分、本校生の中にも”くま鉄LOVE”の生徒がいるはずで、その中には受験の申し込みをした人がいたのでは?ひょっとしたら試験会場でお会いしないかと、ひそかに期待していました。しかし、本校生は誰も会場にいませんでした。きっと、公式テキストブックや問題集等がない中で、どう勉強を進めればいいのか途方に暮れ、断念したのかもしれません。そんな生徒の皆さんに少しでもお役に立てれば・・・、そして同時に、人吉球磨の魅力を少しでも伝えることができればという願いを込めて、ご当地検定大好きで京都観光文化検定2級所持者でもある筆者が「勝手にくま鉄検定」と題して8月末に、120問の問題をアップしました。1回10問の12セット分です。全て4択式で1問10点、10問で100点満点です。
来年2月に実施予定の上級を受験する際に必要な中級の合格通知が、9月末に無事に届きました。そこで、実際に出題されていた初級・中級の問題(試験終了後、回収)も思い出しながら、問題の再構成を図り、10月中旬には「おまけ編」3セットを新作して内 容を補強しました。
中には、多少マニアックな問題も入っていますが、力試しに遊び感覚で解いてみてください。60点以上で初級、70点以上で中級、80点以上で上級、90点以上で特級というのが、この「勝手にくま鉄検定」の合否の目安です。解答と解説付きですから、間違えた問題は本番に備えてしっかり覚えておきましょう。
実際のくま鉄検定の初級・中級は、○×式で出題されていました。上級や特級の出題形式は未発表ですが、4択式の難しい問題で十分に実力をつけておくと、本番では雲が晴れたように簡単に解けるかもしれません。
なお、60点以上で初級、70点以上で中級・・・とか書きましたが、実際の「くま鉄検定」の各級との相関は全くないことをお断りしておきます。
作問に際しては実際に各駅に足を運び取材するなど、考証には力を尽くしたつもりですが、誤植や誤っている箇所等がありましたら連絡していただけると幸いです。
それではさっそく「勝手にくま鉄検定」第1セット目 に挑戦しましょう!
1 くま川鉄道が保有する5つの車両(田園シンフォニー)は人吉球磨盆地特有の四季をイメージして、車両ごとに季節のテーマを設定し、車体色や内装を変えています。次のうち季節名と車両の色の組み合わせが誤っているものはどれですか。
①春・ベージュ色 ②夏・青色 ③秋・白色 ④冬・茶色
2 くま川鉄道の始発駅から終着駅までの営業距離は何kmですか。
①24.8km ②28.4km ③42.8km ④48.2km
3 くま川鉄道の駅構内に乗車以外の目的で立ち入るときは、入場券を購入し、これを所持しなければならないとされています。(この旨がホームページに記載)大人の入場券は一人いくらですか。
①190円 ②200円 ③210円 ④220円
4 くま川鉄道に14ある駅のうち、改札業務などを行う有人駅は、人吉温泉駅を含めて全部でいくつありますか。ただし、午前中の一部の時間帯だけ業務を行う駅も含めるものとします。
①2 ②3 ③4 ④5
5 くま川鉄道は今年(2019年)、開業30周年を迎えました。開業した年である1989年(平成元年)に起きた出来事は次のうちどれですか。
①3月11日に宮城県沖で国内観測史上最大のマグニチュード9.0の巨大地震が発生し、大津波が次々と沿岸部を襲った。
②4月1日、日本ではじめて消費税が税率3%で導入された。
③9月11日に米ニューヨークの世界貿易センタービル等に乗っ取られた旅客機が激突し、犠牲者3千人以上を出す史上最大のテロが発生。
④9月16日に召集された特別国会で民主党の鳩山由紀夫代表が総理大臣に指名され、名実共に政権交代が実現した。
6 くま川鉄道が使っているホームは、旧国鉄人吉駅の何番ホームと何番ホームですか。
①1番と2番 ②2番と3番 ③3番と4番 ④4番と5番
7 水質日本一の川辺川と、日本三急流球磨川の合流地点に架かる鉄橋の名称は何ですか。
①球磨川第一橋梁 ②球磨川第二橋梁
③球磨川第三橋梁 ④球磨川第四橋梁
8 くま川鉄道の現社長、永江友二氏の前職は次のうちどれですか。
①銀行員 ②鳶(とび)職人 ③美容師 ④宮大工
9 観光列車「はぴねすトレイン」が川村駅に到着したとき、出迎えていた近隣の女性たちを何といいますか。
①おもてなし武将隊 ②おもてなしべっぴん隊
③錦町地域おこし協力隊 ④ひとよし温泉女将会「さくら会」
10 くま川鉄道の路線と道路は、ほとんどが踏切で交差しますが、7箇所だけ立体交差をするところがあります。
建設工学では、線路に対して道路が高架橋で通過する場合、オーバーパス、地下道で通過する場合、アンダーバスと称しますが、この7箇所の立体交差を分類したとき正しいものは次のどれですか。
①全てオーバーパス ②オーバーパスが4箇所、アンダーバスが3箇所
③オーバーパスが3箇所、アンダーバスが4箇所 ④全てアンダーパス
いかがでしたか?
それでは、「勝手にくま鉄検定」第1セット目の正解と解説です。
1 ③秋・白色
秋は紅葉からの連想でしょうか、赤い塗装が施されています。
白色で塗られた車両は白秋(はくしゅう)と名付けられています。朝霧が有名な球磨地方の白く立ち込めた霧をイメージした着想なんだそうです。
くま鉄検定の必須暗記事項と思われる「車体番号、季節、カラーリング」の組合せをまとめておきます。
2 ①24.8km
2,4,8って2倍、2倍で最後は八という末広がりの数字になっていて、とても縁起がいい数字の並びだと思いませんか?!かけ算の九九の2の段「ニシがハチ」になっているのも面白いです。
くま川鉄道は1日に14往復運転されていますので、1日の全営業走行距離は、24.8×14×2を計算して694.4kmになります。このおよそ700kmという距離は、熊本市から大阪市までの距離(山陽自動車道経由)に匹敵します。
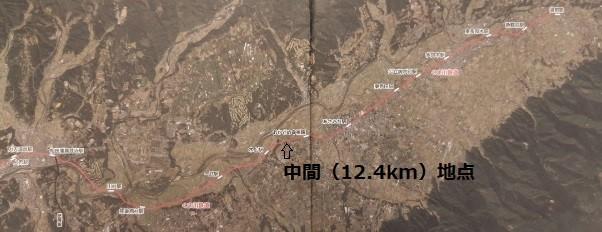
ちなみに、半分の12.4km地点はどこら辺になると思いますか?
下のGoogle Earthで撮影された地図(開業30周年記念冊子の中に収められていた写真)を頼りに、定規を当てながら計測したところ、木上駅とおかどめ幸福駅の間にあることがわかりました。
3 ①190円
入場券に係る料金(入場料金)は、駅構内の秩序や安全に対する対価とされています。今回、確認のため入場券を購入するため人吉温泉駅に出向いて驚きました。くま川鉄道では相良藩願成寺駅を除いて入場券の実質的な販売はしていない(隣の駅までの切符で代用)と聞いたからです。同社のホームページには「乗車以外の目的で入場しようとする場合は、入場券を購入し、これを所持しなければならない。大人・・・190円」とあるのに!

ちなみに、JR九州の各駅の大人の入場券は170円(博多駅と小倉駅は150円)です。鉄道各社で入場券の値段はまちまちですが、最低運賃と同額になっている会社が多いようです。
4 ③4
人吉温泉駅とあさぎり駅は、年中無休で5:30~21:00まで営業を行っています。これに加えて、相良藩願成寺駅が6:00~9:00、湯前駅が6:00~10:00の時間帯(いずれも年末年始・土・日・祝祭日を除く)にあいていますので、全部で4駅になります。
ちなみに、もしこの問題が「券売機が設置されている駅はいくつありますか?」だったら、それら4駅に多良木駅が加わって全部で5駅になりますので、どちらで出題されてもいいように覚えておきましょう。

どうでもいいことかもしれませんが、券売機の値段はいくらぐらいするのでしょう?
調べたところ、機能によって大きく違うようですが、最低でも500万円、定期券なども購入できるものなら2,000万円といったところでした。
ネット上には、券売機のメーカー(オムロン、日本信号、東芝・・・)の外見からの見分け方を詳しく解説してあるサイトもありました。歴史的には、1904年にロンドンのセントラル・ロンドン鉄道で自動券売機が導入されたのが世界で最初なんだそうです。
5 ②4月1日、日本ではじめて消費税が税率3%で導入された。
1989年(平成元年)に導入された消費税は、3%→5%(平成9年)、5%→8%(平成26年)、8%→10%(平成31年(令和元年))のように改定され、平成の歴史と共にあったといえます。
ちなみに、開業の年である平成元年は、昭和天皇が崩御して改元された年ですが、2月24日に大喪の礼が行われ、6月24日に歌手の美空ひばりさんが亡くなり、7月23日には、憲政史上初の女性党首となった故土井たか子委員長率いる社会党が7月23日に参議院において第一党になってマドンナ旋風が吹き荒れた年でもありました。10月14日には田中角栄元首相が退陣を表明し、11月10日には、ベルリンの壁が崩壊しています。
その他の選択肢も念のために確認しておきます。①の東日本大震災は2011年(平成23年)の3月11日です。③の同時多発テロは2001年(平成13年)に起き、④の政権交代は2009年(平成21年)でした。
6 ④4番と5番
くま川鉄道の発着ホームは4番と5番です。1~3番はJR九州の肥薩線の発着ホームです。
ところで、4番と5番の使用頻度はどちら高いと思いますか?
終日に渡って人吉温泉駅で調べてみました。一日に14本の列車が人吉温泉駅から湯前に向けて出発するわけですが、4番線から出発するのはわずか3本(1D、3D、17D)だけでした。なぜこんなにも頻度が違うのか駅員さんに尋ねてみたい気がします。
ちなみに、ホームの番号の割り振り方ですが、現在、法的な規定は無く、鉄道会社が自由に番号を設定してよいようです。しかし、JRに移行する前の国鉄では、駅長室のある側から1、2、3とするよう規定があったらしく、無人駅の場合もこれに準じて、駅舎や待合室のある側から番号を振っていたとネット上の情報にありました。JR化後はこの規定はなくなったそうですが、慣例的に駅長室(駅事務室)側から番号を振る習慣が残っているようです。面白いことに、駅長室の位置が変わっても旧駅のホームの順番を維持するようで、必ずしも駅長室に近いほうが1番線になっていない駅もあります。また、ホームを拡張して、1番線よりも駅長室に近い側にホームができると、「0番線」と表記する駅もあります。
7 ④球磨川第四橋梁
川辺川と球磨川の合流の様子は、この球磨川第四橋梁(全長322m)からしか眺めることができません。その意味でくま川鉄道自慢の絶好のビューポイントであり、観光列車「はぴねすトレイン」では速度を落として運行されるほどのサービスぶりです。
車窓から見ると、写真①のように、川辺川(国土交通省発表:13年連続水質日本一)のほうが澄んでいて、球磨川が濁っていたり、その逆があったりと、上流地区に雨が降ったかどうかなど天気まで分かります。
ちなみに、写真②は写真➀内aの木綿葉(ゆうば)大橋から眺めた球磨川第四橋梁の遠景です。
今回、球磨川第四橋梁を下から見上げた写真をここに載せるべく、何度も合流点付近に足を運び、土手伝いに川岸に降りられる箇所を探しました。苦労の甲斐あってやっと撮影できました。(写真③)このアングルは、球磨川の中に入って鮎釣りをしている太公望だけが見ることができるものかもしれません。
最後に、選択肢➀~➂について補足です。いずれもJR九州の肥薩線にあり、球磨川を跨ぎます。
球磨川第一橋梁(写真④)は、八代方面から人吉に向かっていると鎌瀬駅を出てすぐ渡る鉄橋です。
球磨川第二橋梁(写真⑤)は、球磨郡球磨村の三ヶ浦地区、肥薩線の那良口駅と渡駅の間にあります。
球磨川第三橋梁(写真⑥)は、人吉駅を出て大畑駅に向かう途中で球磨川を渡りますが、そこに架かる鉄橋です。
いずれも赤い鉄橋で印象的ですし、特に球磨川第一橋梁と球磨川第二橋梁は、川の流れに対して直交して架かっていない「斜橋」であることも目を引きます。川を真横に渡るように架けると短い距離ですみ、建設材料も、経費も少なくてすむわけですが、なぜ斜めにかかっているか考えてみるのも興味深いことかもしれません。
8 ③美容師
永江友二氏は、元々人吉市内で美容室を営む美容師という、異色の鉄道会社社長です。美容室を営むかたわら、使われていない古民家を飲食店にリノベーションしたり、一度は途絶えたお祭りを復活させたりといった活動が注目され、請われて社長に就任されました。球磨工業高校の学校評議員も務めていただいています。
くま川鉄道のホームページ上の社長のブログ(2018/07/19)に、社長就任の経緯等興味深い記事があります。ぜひ、読んでみてください。
9 ②おもてなしべっぴん隊
べっぴんとは漢字で「別嬪」と書き、非常に美しい女性のことを言います。この「おもてなしべっぴん隊」は、観光列車が運行を始めた2014年(平成26年)に近隣の女性たちが地域を盛り上げようと「川村駅を勝手に守る会」が結成されたことによります。
今は故人になりましたが、2015年12月、当時93歳の下田幸(しもだみゆき)さんが川村駅の名誉駅長に任命されたことや、べっぴん隊の皆さんが列車の停車中、和装姿で乗客にお茶を振る舞い、手作りのブローチなどを販売している様子などが地元紙で報じられたことがあります。
なお、このおもてなし活動、一定の成果を収めたということで2019年(令和元年)8月31日をもって活動を終了しました。
10 ②オーバーパスが4箇所、アンダーバスが3箇所
これは難しかったかもしれません。まず人吉温泉駅と相良藩願成寺駅の間で2箇所道路と交差します。1箇所目は、県道17号・坂本人吉線(写真①)で、人吉市在住の方ならあの道路のことかとすぐにピンとくると思います。2箇所目は、愛甲産婦人科横にあるバイクや歩行者が主に利用している軽自動車がやっと通れる生活道路(写真②)になります。いずれも道路が地下道で線路の下をくぐるアンダーパスです。
相良藩願成寺と川村駅の間でも2箇所交差します。1箇所目は、県道33号・人吉水上線(石清水跨線橋:写真③)で、2箇所目は、九州自動車道(写真④)です。どちらの写真も列車の運転席横の正面窓から撮ったものですが、これから分かるようにいずれもオーバーパスです。
次に、あさぎり駅と東免田駅の間で町道と交差し(八幡跨線橋:写真⑤)ますが、これは道路が線路の上を高架橋で跨ぐオーバーパスです。
さらに進むと、東多良木駅と新鶴羽駅の間でも2箇所交差があります。
まず、東多良木駅を出てすぐ、百太郎溝沿いの町道(写真⑥)との交差で、道路が線路の下をくぐっていますのでアンダーパスです。
次に、国道219号線(写真⑦:道路側から撮影)と交差しますが、こちらは道路が線路の上を高架橋で跨ぐオーバーパスです。
従って、②オーバーパスが4箇所、アンダーバスが3箇所が正解です。
なお、新幹線は全て立体交差にすることが法律で決まっています。
第2セット目以降の問題は、
メニューにある
校長室より→「勝手にくま鉄検定」にアップしていますのでぜひお楽しみください
クリック→第2セット目以降の問題
8月9日、登校日の様子
いつも本校のHPにお越しいただきありがとうございます。
昨日のテレビで、8月8日は立秋と報じていました。そう聞いて、「こんなに暑いのに秋?何かの間違いでは?」と思った人がいたかもしれません。立秋の日の頃が夏の暑さは全盛期なんだそうです。仕方ありません。
ということで、皆様、残暑お見舞い申し上げます。
今朝、 通勤で通る道沿いに芙蓉(ふよう)のピンクの花が涼しげな佇まいで咲いていました。「今年も咲いたか、ということはもう晩夏だな・・・」とか思いながらパシャリ。芙蓉の花は、朝咲いて夕方にしぼむ「一日花」ですが、つぼみを大量につけて、長い期間をかけて順番に次々と咲いていくため、最初にこの花の名前を図鑑で調べた頃は、そうと気がついていなかったことを思い出します。
ところで、今日8月9日は、長崎の74回目の原爆の日です。学校は登校日で、全員に平和学習のDVDを視聴してもらいました。漫画「はだしのゲン」の作者中沢啓治氏のインタビュー形式のドキュメンタリー、いかがだったでしょうか。中沢さんは広島で生まれ育ち、6歳のときに被爆されたそうです。映像の中で、子どもの目に焼き付いた惨状を生々しく語っておられました。
暑い中、集中して視聴できるか当初心配もしましたが、私語1つ無く真剣に見ていただきました。「平和の尊さを少しでも感じ取ってもらえれば・・・」という担当の先生の思いは十分に伝わったものと思います。
そして、11時15分からは人吉下球磨消防組合中央消防署から消防司令の高畠様を始め7名の署員の方にお越しいただき、職員と運動部活動のキャプテン・マネージャを対象に、救急救命(胸骨圧迫とAED、エキペン)の研修を行いました。
職員は全員が経験者ですが、生徒の中には初めての人たちもいたようです。強く・速く・絶え間ない胸骨圧迫によって、救命率が大幅に向上するという説明に続き、乾電池の長さ(5cm)を例に出され、「胸がそのくらい沈むまで強く押すように」との指示の下、練習をしました。
私、人形が相手なら大丈夫ですが、実際にそういう現場に遭遇したとき、骨折させるのが心配で、正直そんなに強く押せるか今一つ自信がありませんでした。そのことを質問したところ、「たとえ骨折させても、善意の救助者が傷病者などから損害賠償責任を問われることはない」と伺い、ちょっと安心したところです。
最後に、いつものように「小町算ごとき」に挑戦してみます。
最近は1日に1200件前後のアクセスをいただいています。今朝、学校に着いて最初にHPを開けた時(午前7時37分現在)の総アクセス数は1484250でした。
この 1484250 という数字の並びをそのままにして、加減乗除等の記号を入れて、今日の日にち8月9日の数字をそのまま並べた89を作ってみます。
1-4+84+2+5+0!=89 → 8月9日
あまりにも簡単にできたので拍子抜けです。ということで、もう1つ。
148÷4+2+50=89 → 8月9日
調子にのってあと1つ。
1-√4-8-√4+2×50=89 → 8月9日
今日はなぜか冴えているようです。もう一つ
(1+4)×8×√4+2×5-0!=89 → 8月9日
まだ何通りもできそうな気がしますが、キリがないのでここら辺でやめておきます。生徒の皆さんだったらどのような式を作りますか?3年生は、就職試験のSPI対策として、ぜひ考えてみてください。
夏休みも既に半分が過ぎたことになります。明日から夏休みの後半戦、そろそろ宿題が気になっている人もいるかもしれません。いい夏をお過ごしください。
【校長】
体験入学と夏越しの祓
いつも本校のHPにお越しいただきありがとうございます。
「全国的に危険な暑さ!」と盛んにテレビが報じていますが、いかがお過ごしですか。
そんな暑いさ中、今日、学校では体験入学をメインに、ものづくり体験教室や寮見学会が開催されました。生徒・保護者、引率の先生も含めて400人近くの参加があり、中には遠路、関東方面からお越しいただいている生徒さんもおられました。ありがとうございました。熱中症の発生も懸念されたところですが、皆さんそれを跳ね返す位の熱意を持って参加していたように思います。
いかがだったでしょう、楽しんでいただけましたか。来年、ものづくりを学ぶ本校に入学したらどのような学校生活を送ることになるか、少しはイメージが湧いたでしょうか?中学生の皆さんたちの進路決定の参考になったら嬉しいです。
説明などのお世話をしていただいた3年生の皆さん方もお疲れ様でした。育友会から、お昼の弁当を支給していただきました。ボランティアのお礼ということでしょうか?
写真は、開会式と建築科での鉋がけ体験の様子です。
ところで、早いもので7月も今日で終わりになります。今日、学校のすぐ下にある青井阿蘇神社(国宝)で「夏越しの祓(なごしのはらえ)」が開催されると聞いていたので、放課後、ちょっと様子を見に行ってきました。神事は夕方5時半からということで、残念ながら参加することはできませんでしたが、写真のとおり、茅(ち)の輪の組立も終わり準備万端といった様子でした。
7月1日の記事にも書いていたように、夏越しの祓は、正月から半年間に知らず知らずにたまったけがれや罪を落とし、その後の半年間を健やかに過ごせるように願って、浅茅(あさじ)で作った大きな茅の輪をくぐる神事のことです。
青井阿蘇神社の場合、HPによると、鎌倉時代の至徳3年(1386年)相良7代藩主前頼(さきより)の時代に始まり、一時中断しましたが、室町時代の天文2年(1533年)16代藩主義滋(よししげ)により再興され、現在まで600年以上連綿と続く伝統的神事とありました。
最後に、いつものように「小町算ごとき」に挑戦してみます。
今朝、学校に着いて最初にHPを開けた時(午前7時26分現在)の総アクセス数は1471663でした。この 1471663 という数字の並びをそのままにして、加減乗除等の記号を入れて、今日の日にち7月31日の数字をそのまま並べた731を作ってみます。
1-4+71+663=731 → 7月31日
あまりにも簡単にできたので拍子抜けです。ということで、もう一つ。
|147×(1-6)|-6!!!!÷3=731 → 7月31日
夏休みも既に4分の1が終わりました。明日から8月。皆さん、いい夏をお過ごしください。
【校長】
【注】 中学生の皆さんへ
2つ目式の中にある"||"の記号は「絶対値」です。中学1年の数学で正の数、負の数を学習したとき、この言葉は見受けたことがあるはずです。数直線上の(原点との)距離(の差)を表し、|-4|=4とか学習しましたよね!
絶対値の問題では、絶対値の記号"||"をはずして計算をすることが多くあります。そのはずし方、3通りあります。
①絶対値の中が0より大きい場合は、|3|=3のように絶対値の記号をはずすだけ。②絶対値の中が0の場合は、|0|=0のように0になります。③絶対値の中が0より小さい場合は、|-4|=|(-1)×(-4)|=4のように、中の数字に-1をかけてから絶対値の記号をはずします。-をとるのではなくて、-1をかけるというのが"みそ"です。
いつだったか、1年生のある教室で、|√2―2|の絶対値をはずす数学の授業を廊下越しに見ました。√2はおよそ1.414です。それから2を引きますので絶対値の中は0より小さくなります。従って|√2―2|=|(-1)×(√2―2)|=-√2+2(=2-√2)となります。中学生の皆さんにはちょっと難しいかもしれませんが、大丈夫ですよね!
ものづくりコンテストの練習廃材から
暑中お見舞い申し上げます。
夏休みに入って早くも1週間が過ぎようとしています。夜、寝る前に振り返ったとき、納得いく一日一日が送れていますか?
さて、気付いている人がいるかもしれませんが、先日来、建築科のピロティに見慣れないベンチが置いてあります。
よく見ると、先日開催された高校生ものづくりコンテストの「木材加工部門」の課題作品を組み合わせて製作したものみたいです。

ここで敢えて紹介しなければ、これが廃材からできているなんて、分からなかったのではないでしょうか。
3つのベンチが並んでいましたが、特に一番左側の八角形のベンチが素敵だと思います。高校の日本史で「古代の天皇陵(古墳)は八角形のものが多い」と習って「そうなんだ!?」と思って以来、私、八角形を見ると特別な反応をするようになりました。風水関係の本で読んだことですが、八角形は全方位を象徴していて、森羅万象から幸せのエネルギーを引き寄せることができるという意味で特に大切にされ、「風水のシンボル」と呼ばれているようです。中でも、八角形のフレームの鏡は、全方位から幸せを引き寄せて、運気がアップしたり、金運が上がったり・・・といった効果があるんだそうです。
梅雨が明け大変暑い最中、建築科の木材加工室では、伝統建築専攻科2年の川口君と1年の和泉君が来る7月31日から福岡市のマリンメッセ福岡で開催される「第14回若年者ものづくりコンテスト競技大会」に向けて、黙々と練習に励んでいました。八角形のベンチが勝運を引き寄せて、良い成績が出ることを祈っています。
話は大きく変わりますが、ものづくりコンテストは木材加工部門に限らず、旋盤部門でも電気工事部門でも、練習をとおしてかなりの廃材が出ます。その再利用のアイディアや技術を競うものづくりコンテストをするときっと面白いのでは、といつも思っています。
実際、「古くなってしまったものを、別の新しいものとして蘇らせる」ことを目的とする様々なコンクールが開催されています。山形県では、使用済み自動車の3万点からなる部品の再利用、再資源化等をテーマとしたものづくりコンテストが実施され、山形工業高校が「エアバッグを再利用した車イス」を製作して、並み居る高専や大学を押さえて最優秀賞を受賞したというニュースをつい先日も目にしました。
ものづくりコンテストの廃材を活用したものづくりコンテスト、できないものでしょうか?いつか工業校長会で提案してみたいと思います。
【校長】
面接の練習が行われています
1学期も残り1週間を切りました。蒸し暑い昼下がり、校内のあちこちから「失礼します」と大きな声が響いてきます。写真は機械科の面接の練習の様子です。
本校の面接の練習は、各科ごとに専門科目の授業や実習等から少しずつ時間を捻出して行うものと、全職員に生徒数名を割り振って行う2系統で行っています。私がこれまで勤務した学校では、全職員が面接に関わる方式は経験ありません。本校だけの特色あるキャリア教育の取組かもしれません。
ところで、面接の練習の功罪、色々と言われています。企業関係者からも「志望の理由など棒暗記してきたものをオウム返しに言うだけで、ちょっとイレギュラーな質問をすると返答に窮する」などと、面接の練習をやり過ぎて「面接慣れ」していることについて、時として厳しい御意見を伺うことがあります。おっしゃることは、私たちも前期(特色)選抜等で中学生受験者に面接をしていて、全く同じことを感じることがままあり、よく分かります。
でも、だからと言って、面接の練習を全くせずに、就職試験に臨ませることは躊躇します。やはり、当日の緊張を和らげ、事前に会話の印象を確認できるなどのメリットも大きく、適度な練習は欠かせないと思っているからです。生徒の皆さんは、友人や家族に面接官役をお願いする、録画して確認する…などの方法も使って、客観的な意見をもらいながら練習を深めてください。
建築科伝統建築コースの生徒たちの面接の練習は、午前中にあっていたそうです。宮大工希望の生徒もいるはずです。
図書館にある菊池恭二著「宮大工の人育て」のp.212~216には、「採用では、一に真面目さ、二にやる気と覚悟」と題して次のような記述がありました。これを読むと、「面接は虚々実々だ!」とまで言ったら大げさかもしれませんが、採用側と受験生との一対一の真剣勝負であることがよく分かります。一部を引用します。
弟子を取るときは採用面接を行います。工務店の子どもさん、公務員の子どもさん、いろいろな人がきます。学歴はいっさい関係ないし、ペーパーの試験をやるわけでもありません。弟子にするかどうかは基本的に面接のみで判断します。決めては何かといったら、一に真面目さ、二にやる気と覚悟、これに尽きます。それがどれだけあるかを基準にして見ます。あとは宮大工という特殊な職人の世界でやっていけそうかどうか、その適性です。・・・(中略)・・・
やる気と覚悟を見るためにあえて突き放した厳しいことも言います。「宮大工になったって普通の住宅みたいに仕事があるわけじゃない。先々どうなるかわからないし、ある日突然、仕事が全然なくなるかもしれない。それでは彼女がいたって結婚もできやしない。それこそ結婚して子どもでもいたら、どうやって家族食わしていくんだ。早く一人前になって独立したいなんて夢を描いてるかもしれないけれど、そんな甘いもんじゃないぞ」
その一方で、「やる気と実力さえあれば、いくらでもいい思いもできるよ」と大きな夢も語って聞かせます。「宮大工は、野球の選手や相撲の力士なんかと同じように、実力次第でいくらでも稼げるし、歴史に残るような仕事もできる。千年後の人たちに自分の名前を残すことだってできる。本人の努力次第で名のある棟梁にもなれるし、大きな工務店の経営者にだってなれる。宮大工にはそういう大きな夢があるぞ」
厳しい現実と夢の迫で、子どもたちの顔には不安や希望の表情が微妙に交差しながら浮かんできます。それを見逃さず、読み取るようにしています。
今年も今日から後半戦
早いもので、今年も半分終わってしまいました!
後半戦の第1日目、大雨洪水警報や土砂災害警戒情報が発令され「記録的豪雨に最大級の警戒を」ということで、休校(家庭学習)の判断をしました。校内は今、ひっそりとしています。
6月26日(水)に、平年に比べて21日も遅い、最も遅い梅雨入りとなったわけですが、いきなり熱帯低気圧の通過による大雨による被害を心配したり、「線状降水帯」という聞き慣れない気象用語を耳にしたりしています。農家にとっては恵みの雨かもしれませんが、安全確保に留意しながら自然とうまく付き合う必要があると痛感します。明日の朝も大雨が予想されています。今日のように、午前6時半までに学校をどうするか判断して学校安全メールで通知する予定です。
ところで、1年の折り返しに当たる昨日6月30日(日)は、「夏越しの祓(なごしのはらえ)」でした。各地の神社では、正月から半年間に知らず知らずにたまったけがれや罪を落とし、その後の半年間を健やかに過ごせるように願って、浅茅(あさじ)で作った大きな茅(ち)の輪をくぐる神事が行われています。この日本神話に基づく祭事、私も久々にしようと思って、昨日の夕方、青井阿蘇神社に行きました。そしたら「うちは7月31日にやっている」とのこと。熊本の神社は、ほとんど旧暦で行っているようです。ちなみに、青井阿蘇神社のHPには次のようにあります。
当神社の夏越祭は、鎌倉時代の至徳3年(1386年)相良7代藩主前頼(さきより)の時代に始まり、一時中断しましたが、室町時代の天文2年(1533年)16代藩主義滋(よししげ)により再興され、現在まで600年以上連綿と続く伝統的神事です。
生徒の皆さんにとっては、茅の輪をくぐると言っても、写真がなければイメージができない人がほとんどだと思います。今度7月31日にお参りに行ければ、写真を添えてまた報告します。
昨日もう一つ残念だったのは、「水無月(みなづき)」という伝統的な和菓子を食べそこなったことです。昨年、京都検定の受験勉強を通して知ったことですが、京都では水無月と呼ぶ、ういろうの上に邪気を祓うあずきをのせた三角形のお菓子を夏越しの祓の日に食べる習慣があります。人吉の和菓子屋さんでも6月30日の限定で販売しているお店があると聞いていたので、神社の帰りに買い求めに行ったら、何と「完売!」とのこと。ということで、こちらも写真を示せず、どのようなお菓子かイメージが湧かないかもしれません。京都検定の公式テキストには「水無月」について以下のような趣旨の説明があります。
昔、宮中では旧暦6月1日に「氷の節句」が行われていました。冬にできた氷を山間の氷室(ひむろ)に貯蔵しておき、そこから取り寄せた氷を口にして夏を健康に過ごせるよう祈るというものです。しかし、庶民にとって氷は高嶺の花。そこで氷をかたどった三角形の生地に厄除けの小豆を散らしたお菓子が作られたのです。「水無月」は庶民の氷へのあこがれからできた銘菓。現在では夏越の祓の日の和菓子として親しまれています。
枕草子には清少納言がかき氷を楽しむ様子が記されています。平安時代の暑気払いなのかもしれません。私、行事食は大切にしたいと常々思っています。皆さんは、水無月、食べたことがありますか?
【校長】
夏至の日を求める計算式
今日6月22日は夏至(げし)。
北半球では、1年のうちで最も昼の時間が長くなることで知られています。
長い説明は不要と思いますが、暦のうえで1年を24分割し、それぞれに季節を表す言葉をつけた二十四節気という季節の呼び方があり、そのうちの一つが夏至です。例年6月21日頃と記憶しています。でも、年によって1日位前後することがあるので、今年はいつだろうと毎年調べなければなりません。
これは誰がどんなふうに定めているんだろうと思って、今さらながら色々調べてみました。1日位前後する理由がごちゃごちゃ解説してあるサイトがありましたが、中学理科以来、天体の分野が苦手だったので敬遠(パス)しながら、やっと辿りつきました。
知りませんでした。やはりあるんですね。計算式が。次のような式でした。
=INT(22.2747+(0.24162603*(Y-1900))-INT((Y-1900)/4))
Yに夏至を調べたい西暦年を代入します。例えば今年(2019年)なら、
=INT(22.2747+(0.24162603*(2019-1900))-INT((2019-1900)/4))
となります。手元の電卓で計算をしてみます。
=INT(22.2747+28.75349757-INT(29.75))
となります。ここでINTは、「指定した数値を超えない最大の整数を返す」関数です。正の数の場合*、小数点以下の端(はした)を切り捨てる関数と言ってもいいです。
従って、INT(29.75)=29となり、これを代入してさらに計算を進めます。
=INT(22.2747+28.75349757-29)
→ =INT(22.02819757)
→ 22
おお、確かに!!
この、INT(インテジャー(注:イントと読まれる方もいます))という関数、教壇に立っていたころは、エクセルの実習で消費税率をかけて端を切り捨てる場面等で指導していたことがありましたが、久々に目にしました。関数名は、整数のことを英語でintegerと綴りますので、きっとそれに由来しているのでしょう。
*正の数の場合は、INT(3.33)=3となります。でも、負の数の場合、INT(-3.33)=-4となるので注意が必要です。
この計算式、「1904年から2099年まで使える」とありました。楽しそうですので、エクセルを使って色々と計算してみました。
その結果、1992年から2019年までの夏至は21日~22日ですが、2020年から2055年までは全部21日でした。そして、2056年から2099年の中には、しばしば20日の日があるようです。
「NASA(アメリカ航空宇宙局)などで使われる厳密な計算式よりもかなり精度が落ちる式」とか紹介されていましたが、厳密な計算式とはいかなるものか興味が湧いたところです。
ところで、今日6月22日、19時14分現在の総アクセス数は1415669でした。
いつものように、この 1415669 という数字の並びをそのままにして、加減乗除等の記号を入れて、今日の日にち6月22日の数字をそのまま並べた622を作る「小町算ごとき」に挑戦してみます。
INT(141÷5)+66×9=622 → 6月22日
使ってしまいました。INTを。ちなみに、この「小町算ごとき」で初めてINTという関数を使ったような気がします。生徒の皆さんだったらどのような式を作りますか?
梅雨入りもせず、夏はまだまだこれからが本番というのに、今日を境に日が明るい時間が一日一日短くなるということで、少々メランコリックな思いもしないわけではありません。皆さん良い週末をお過ごしください。
【校長】
なすに悶絶!?
図書館に配架してある料理雑誌「オレンジページ」の6/17号の特集記事は、「なすに悶絶」。何とキャッチーなタイトルなんでしょう!
なすびは、煮る、炒める、焼く、蒸す…と、どんふうに調理をしてもお箸がとまらない料理ばかりで、私、とても好きな野菜です。でも、「身悶(みもだ)えするほどのなすび料理とは一体どんな料理?」、タイトルにつられてパラパラと写真を眺めてみました。
凄く美味しそうで、心を捉える料理の写真がありました!レシピをさっそくメモ。この週末に作ってみるつもりです。なすびは、夏野菜を代表する存在です。これから旬の味を大いに楽しみたいと思っています。
なすび料理が好きな生徒の皆さん、図書館に足を運んで「オレンジページ」をめくってみてはいかがでしょうか。
ところで、3週間ほど前、校庭の花壇に植えたなすびが写真のように、かなりしっかりと葉を広げてきました。
2ヶ月後?の収穫に向けて、夏場の水やりが大変ですが、校長室の掃除の生徒たちにも手伝ってもらいながら心を込めて育てるつもりです。何事も根気がいるのは人材育成と同じです。
ところで、本日6月21日、午前8時33分現在の総アクセス件数は、1414213
有名な数字の並びです。何でしょう?
ヒントです。
最初の1と4の間に小数点を入れると、1.414213
もうお分かりだと思います。√2の近似値でした。
そういう思いで先ほどのなすの若葉の写真を眺めてみます。葉の先端と茎を結ぶ三角形を想像してみると、辺の比が1:1:√2の直角二等辺三角形が浮かび上がってくるから不思議です。考えすぎかもしれませんが、見れば見るほど√2です。3つの星が「くし団子」のように並んでいたら、オリオン座にしか見えない悲しい習性と似ているのかもしれません。
話は大きく変わりますが、生徒の皆さん。
√1=1
√2=1.414214356(一夜一夜に人見頃)
√3=1.7320508(人並みに奢れや)
√4=2
√5=2.2360679(富士山麓オウム鳴く)
√3の「人並みに奢れや」や、√5の「富士山麓オウム鳴く」の語呂合わせは、とてもよくできていて納得もできると思いますが、√2の「一夜一夜に人見頃」はどういう意味か分かりますか?中学校でどう説明を受けてきましたか?
私は中学校のときの数学の先生がどういうふうに説明をしてくださったのか、さっぱり思い出せないのですが、勝手に次のように解釈して生徒にも教えていました。
春に桜が咲きつつあるときは毎日毎日、少しずつ花が開いていくので、「一晩(夜)一晩(夜)経つごとに人が見て、どんどん丁度よい頃合いになっていくものだな~」⇒「一夜一夜に人見頃」
今日改めて、ネットを色々と調べていたら、次のような解釈をしている方がいらっしゃいました。とても優雅な解釈で感動したので一部を引用して御紹介します。
春を過ぎ、初夏から夏にかけて、夜ごとに華やいでゆく街の風情が目に浮かびます。描かれているのは、単なる風景ではありません。街の賑わい、人々の暮らしなのです。
花を見るのでも月を見るのでもありません。人なのです。人を見ているだけで嬉しくなるような、そんな季節になろうとしているのです。
人々は解放的であり、くつろいでいて、穏やかで、平和で、この先に対する希望を持っている。しかも、変わってゆく。
わずか12音節で、人間の生活の場としての街を 、そのゆったりとした時間の中の変化を、一瞬一瞬の大切さを、希望を、人と人とのつながりを、人間への興味を 生き生きと描いています。
最後に、いつものように 1414213 という数字の並びをそのままにして、加減乗除等の記号を入れて、今日の日にち6月21日の数字をそのまま並べた621を作る「小町算ごとき」に挑戦してみます。
14!!!!+14!!!!!!+2-1+(3!)!!!=621 → 6月21日
ちなみに、大丈夫と思いますが、14!!!!は、14の4つ飛ばしの階乗ですから、14×9×4を計算して504となり、14!!!!!!は、6つ飛ばしの階乗ですから14×7を計算して98です。
皆さんだったらどのような式を作りますか?
【校長】
祝 総アクセス数 140万件達成
いつも本校のHPにお越しいただき、ありがとうございます。6月に入り蒸し暑さを感じる毎日が続いていましたが、今日は朝から凄い雨!
そんな本日6月7日、午前8時2分現在の総アクセス件数は、1400000
140万! 久々にきりのいい数字です。こういう綺麗な数字を見ると無性に素因数分解をしてみたくなります。100万(105)が、25×55で、14が、2×7ですから簡単です。
1400000=26×55×7
従って、その約数は、1, 2, 4, 5, 7, 8, 10, 14, 16, 20, 25, 28, 32, 35, 40, 50, 56, 64, 70, 80, 100, 112, 125, 140, 160, 175, 200, 224, 250, 280, 320, 350, 400, 448, 500, 560, 625, 700, 800, 875, 1000, 1120, 1250, 1400, 1600, 1750, 2000, ・・・(途中省略)・・・20000, 21875, 25000, 28000, 35000, 40000, 43750, 50000, 56000, 70000, 87500, 100000, 140000, 175000, 200000, 280000, 350000, 700000, 1400000
の84個あることになります。
では、いつものように 1400000 という数字の並びをそのままにして、加減乗除等の記号を入れて、今日の日にち6月7日の数字をそのまま並べた67を作ることに挑戦してみます。
1+4(0!+0!+0!)+0!+0!=67 → 6月7日
勿論、0!=1で、これは定義(決めごと)ですから「どうしてそうなるのかなぁ?」なんて考えたらいけません。
実は・・・、6月に入って1日当たりのアクセス数が平均840件位で推移していましたから、「140万件に到達するのは6月9日頃かな?もし10日になったら、610という数字はどうやって作ろうか・・・」とか思いながら、次のような式を心温めていました。
14×{(0!+0!+0!)!-0!}-0!=69 → 6月9日
ところが、どうしたことか一昨日(6/5)が2,900件、昨日(6/6)が3,080件というように、急激にアクセスが増えたので、朝から慌てて式を考えたところでした。皆さんだったらどのような式を作りますか?
話を変えますが、生徒の皆さん、140万という数字に何か心当たりありませんか?
ヒントです。高校入試の理科で必ず覚えておかなければならい数字です。
もう思い出しましたか?
答は、太陽の直径でした。140万km(地球の直径の約100倍)です。これと、太陽の表面温度である約6000度、地球と太陽の距離の1億5千万km、この3つの数字は太陽に関して必ず暗記してきたはずです。
【校長】
木くずの処分

建築科の先生に聞いたところでは、地元の業者が喜んで引き取って行かれるそうです。学校としては無料で処分できるので、お互いwin・winの関係と言えると思います。
でも、通販のサイト等を全国の様々な業者を調べていたら、それらの木くず、アウトドア時の点火用やクッション等の緩衝材、ペットのトイレ、・・・果てはクワガタ・カブトムシの飼育マット等として結構いい値段(200gで400円とか)で販売されているようです。特に、殺菌性や吸湿性に優れている檜(ひのき)の鉋くずは、お風呂やお部屋の消臭などで需要が多いようで、30g(大体、餃子1個分の重さ)で2,500円などかなり高い値段をつけて販売している業者もいて驚きです。ゴミ・産業廃棄物とリサイクル資源、商品の分かれ目は、木の種類やくずの形状・大きさによる分別かもしれません。
話はかわりますが、昔、自宅を新築するに当たって住宅展示場に見学に行ったとき、本物の木造住宅の現場の見分け方は、「現場に木くずがあるかどうか」と説明を受けて、「何を当たり前のことを言っているのか?」と疑問に思ったことを思い出しました。
それほどホンモノの木による家造りではなく、工業製品や既製品など「木に見えるモノ」による家づくりがあるということでしょうか?
【校長】
久々の新幹線で驚いたこと2つ
5月20日(月)から23日(水)にかけて、全国工業高等学校長会総会などに出席するため新幹線で上京しました。熊本から東京まで7時間余りかかりますが、その時間を活用してまとまった仕事ができるので、利用しない手はありません。今回、数ヶ月ぶりに新幹線に乗ってビックリしたことが2つありました。
1つは、警備会社のガードマン(警備員)が結構頻繁(10分おき位)に巡回してきたことです。昨年の6月9日、神奈川県内を走行中の東海道新幹線で発生し、日本中を震撼させた無差別殺人事件を受けての対応だと思いました。
飛行機のような厳重なセキュリティチェックを、手軽さが求められる新幹線に適用することが技術上困難な現状では、精一杯の対応かもしれません。でも、運行中の全ての新幹線にガードマンを雇用する費用も莫大なものになり、そのうち運賃に跳ね返ってくるのではとも思ったところです。安全をお金で買うと思えば、許容すべきなのかもしれませんが・・・。
もう1つは、車内アナウンスです。ネィティブによる録音に加えて、車掌さんが肉声で英語のアナウンスをしていたことです。こんな感じです。
”We are stopping at Kyoto station. The doors on the right side will open.”
全ての路線(九州新幹線【JR九州】、山陽新幹線【JR西日本】、東海道新幹線【JR東海】)でその放送が流れたので、往復で10人ほどの車掌さんの英語を耳にしました。
中には「ウィ アー ストッピング アッ ・・・」のように、カタカナを棒読みされているような車掌さんがいて「これはご愛敬かな?」と思った反面、飛行機のパイロットやキャビンアテンダントのアナウンス並みと言えばいいのでしょうか、抑揚も付けながらとても流ちょうに喋る車掌さんもいて「凄いな!」と感心しきりでした。様々な日本人の英語を聞いて結構楽しかったです。
興味を持ったので色々検索していたら、JR東日本の車掌さんの中には、突発的な事故に伴う遅延情報まで英語のアナウンスされる方がいて、乗客が録音した音声がユーチュブにアップされていることも知りました。「公共放送とはいえ、自分の音声が知らないところでネットにアップされるとは、車掌さんも大変だな・・・」と同情しきりです。
23日に大宮(埼玉県)から東京に帰るときのことです。大変滑らかな英語が聞こえてきました。きっとその車掌さんだったのかもしれません。時間どおりの運行だったから遅延情報はありませんでしたが、「お忘れ物に注意してください」など他の路線にはない次のような英語も付け加えられました。
”We are now approaching to Tokyo. Please make sure not to forget any belongings. Thank you.”
427日後に迫った東京オリンピック・パラリンピックに向け、都内では各案内が複数言語で記されているのをあちこちで見受けましたが、鉄道各社も外国人旅行客のことを本気で意識し始めたのだと思ったところでした。
そう言えば、全国工業校長会総会の後に行われた講演でも講師が英語の大切さについてしきりに訴えられました。このことについては、いつか生徒の皆さんにも話をするつもりです。
また、新幹線の中で読んだ本にも、工業高校生が身につけておいてほしい力について「現在のグローバル化の中で、せめて英語のマニュアルはある程度読めるくらいの力や、英語で書かれた図面もある程度読めるような力がほしい。また、海外に出たときに簡単な技術者同士の会話ができるようにしてほしい」とか書いてありました。
英語はこれからますます大切になってきます。生徒の皆さん、心して勉強してください。
【校長】
思い出深い因数分解
中間考査が終わり、またいつもの球磨工の風景が拡がっています。総体まで2週間、グラウンドには大きな声が響き、どの部活動も活気を帯びています。そして、ものづくりコンテストまで一ヶ月、こちらはどこまでも静寂で真剣な表情が冴え渡っています。
話を大きく変えます。3限目に3階(1年生)の考査の様子を見て回っていたときのことです。1年生の廊下に整然と並べられた教科書やノート類が吹き抜ける風に煽られて開いてしまい、たすき掛けで何度も苦労しながら因数分解を解いた跡がヒラヒラと揺れながら見えたような気がしました。高校1年生1学期の中間考査の数学といったら、どこの学校も「展開と因数分解」がお決まりです。
この記事を読んでいる中学生の皆さんはピンとこないかもしれませんが、高校の因数分解はaX²+bX+cを(pX+r)(qX+s)の形に因数分解する「たすき掛け」とか出てきて、直勘が外れる(運が悪い)と何通りもやるはめになります。結局は単なる「計算技術」なんですが、なかなかできずに「こんな勉強、将来何の役に立つんだ!」といらついてしまった経験が誰しもあるかもしれません。
結論から言うと、大いに役に立ちます。
例えば、「X²+5X+6 を因数分解しなさい」というのであれば、足して5、掛けて6になる2つの数(因数)を見つけ出して、かけ算の形に変形させるわけで、その数は2と3ですから、答えは(X+2)(X+3)となるわけで、確かにこんなふうに習ったことをそのまま使う機会というのはほとんどないかもしれません。でも、社会人になって仕事をしていくと、論理的に物事を考え、分析して整理する場面が色々なところで出てきます。そのような時に、因数を見つけて分解するという考え方がとても大事になってきます。
ここでその具体例を挙げて説明をするのは、長い話になりますので今日はやめておきますが、因数分解の問題を解くために必死に思考する経験そのものは、将来に向けて今やっておかなければならない貴重な訓練であることは間違いありません。難しい問題でもまずは必死に考えてみてほしいと思います。振返ってみたら「あれ?そういえばこれってあの時やっていたことでは…」なんていうことがあるものです。
ところで、私にとって「思い出深い因数分解」があります。高校1年のときの数学の先生(故人)が「8秒で因数分解しなさい」と言って、にこにこしながら中学校レベルの式を板書しました。定数項が結構大きな数字です!
X²-12X-864
皆さん、足して-12、掛けて-864になる2つの数を8秒内で見つけることができますか?
864を素因数分解して約数の組み合わせを考えていたら、とても8秒内ではできません。何とこれは次のように「平方完成」を応用した因数分解になります。
「平方完成」は、2年生以上の人は大丈夫だと思いますが、1年生は次の単元が二次関数でそこで詳しく習うはずです。でもやっていることを見ると「なるほど!」と、必ず分かってもらえるはずです。
X²-12X-864
=(X-6)²-36-864
=(X-6)²-900
=(X-6)²-30²
=(X-6-30)(X-6+30)
=(X-36)(X+24)
その先生がおっしゃるには、どこかの私立高校の入学試験問題で問1によくある雑多な問題を集めた中の1問として実際に出題されていた問題なんだそうです。
平方完成して2乗の差に持ち込み、和と差の積に仕上げるとは何とエレガントで心憎い因数分解なんでしょう!
そんなことを思い出していたら、一昨日、読者(中学生)から学校にお礼のファクスが届いていました。
5月7日の記事で1369が37²であることについて触れていましたが、「その記事を読んでいたからテストの問題が解けました!」という嬉しい報告です。
「X²-16X-1305 を因数分解しなさい」という問題だったそうです。
X²-16X-1305
=(X-8)²-64-1305
=(X-8)²-1369
=(X-8)²-37²
=(X-8-37)(X-8+37)
=(X-45)(X+29)
「こんな問題をテストに出題している中学校があるんだな・・・、日本は広いな!」と私のほうが驚いたところでした。
そういえば、「9991を素因数分解せよ」といった結構大きな数を素因数分解させる問題があったことを思い出しました。小さい素数から順々に割り切れるかを調べていたら、いずれ答えにたどり着けるはずですが、時間がかかり過ぎます。この場合、(平方数)-(平方数)の形で処理できないないか考えてみる手があります。即ち
9991
=10000-9
=1002-32
=(100+3)(100-3)
=103×97
103も97も素数ですからここで終了です。どこか、考えが共通するところがあるような気がします。
【校長】
衣ほすてふ
今日は朝から気持ちよく晴れ渡っています。今朝のテレビで見た天気予報では、沖縄地方を除いてほぼ日本全国「五月(さつき)晴れ」なんだそうで、この言葉の意味について女性キャスターが解説していました。
それによると、旧暦5月(今の6月)が梅雨のころにあたるところから、もともと「五月晴れ」は「梅雨の合間の晴れ間」を指していたのが、時が経つにつれ誤って「新暦の5月の晴れ」の意味でも使われるようになり、この誤用が定着したらしく、放送業界では5月の晴れ間も「五月晴れ」と呼んでいるそうです。
「五月晴れ」といえば、百人一首の第2番にとられている持統天皇(645~702年)のこの歌を思い出します。
春すぎて 夏来(き)にけらし 白妙(しろたへ)の
衣(ころも)ほすてふ 天(あま)の香具山(かぐやま)
「京都おかき専門店 長岡京 小倉山荘 百人一首講座」のサイトから現代語訳と解説等を一部引用します。
「天の香具山」は奈良県橿原市にあり畝傍(うねび)山、耳成(みみなし)山と並ぶ大和三山のひとつです。天上から降りてきたという神話があるので「天の香具山」と呼ばれますが、持統天皇が政治を執り行っていた藤原京からは、東南の方角にこの山が眺められたようです。
この山を見ながら、この有能な女帝は「ああ、いつのまにか春が過ぎて夏がやってきたようね。夏になると真っ白な衣を干す天の香具山に、衣がひるがえっているのが見えるから」とふと感じたのでしょうか。
折しも「令和」効果で万葉集や奈良時代ブームですが、この歌も原歌は万葉集にあり、季節の推移を歌った多くの歌々の中でも、古くから特に名高い歌だったんだそうです。白が印象的で、涼しげな感じが出ていて好きな歌です。
ところで、今日は保健室の前に「白い衣」ではなく、布団が干してありました。
生徒の皆さんはどのくらいの頻度で布団を干しますか?
健康な人は寝付くまでに10分くらいかかるそうです。快適な睡眠のためには寝具も重要なアイテムなんですが、ふかふかの布団で寝る時ってとても気持ちいいですよね。お日様の下で干した布団は、汗などの水分やカビなどが紫外線によって消毒されるからでしょうか、全体の重さが軽くなったような感じがしますし、何とも言えないいい匂いもして、さらにいい気持ちで眠れるような気がします。
ということで、私、天気が良い日は努めて布団を干したいところですが、朝から干して学校に出ても、昼間に帰って布団を取り入れることがなかなかできないので、結局土・日しか干すことしかできません。しかも所用で人吉に残っている時で天気が良い日となると1月に1回位しか干せずに残念です。
これは、平成最初の頃の前任校(天草工業高校)の寮の思い出です。
終日晴れそうな日には朝から寮長の「今日は良い天気です。布団を干しましょう!ベランダに布団を掛けて、お日様に当てましょう!きっといい気分で眠れます!」という放送によるかけ声で寮生が一斉に布団を干していました。寮生たちは、昼休みに三々五々寮にもどって布団をしまっていたわけです。花粉症の人にとっては、布団に花粉が付くことを心配もしましたが、とても良い習慣だなと思っていました。
人吉高校との共同寄宿舎「凛然寮」の寮生の人たちはいかがでしょうか。土日は帰省や部活の練習試合や大会等があり、なかなか布団干しができないのではと心配します。
もう花粉症の季節はほぼ終わりました。今日は試験ですから、部活の練習も早めに切り上げて帰寮するのではないかと思います。数時間でも布団を干してみてはいいかがでしょう?ふかふかのお日様の匂いが、寮生のくせになりますように。そしてぐっすり眠って、明日のテストも頑張れるといいですね。
【校長】
10連休が終わって・・・
皇位継承に伴い降って湧いたような10連休、とうとう終わりました。夏休みの4分の1にも匹敵する長い休み、「令和」のスタートにふさわしい思い出深いものになりましたか。そして、有意義に過ごせましたか?
毎年、4月末~5月上旬の大型連休は疲れが出やすく、学校に行きたくないという気持ちを自覚する時期でもあるとされますが、皆さんは今日どのような思いで登校したのでしょうか。少々心配しています。
先月末(4月25日)発行の「ほけんだより4月号」に、そのような時の心の持ち方について特集してありました。心配な人はもう一度よく読んで、心のケア(あせらない・がんばりすぎない・一人で悩まない)を心掛けてください。
話を大きく変えます。昨日(5月6日)午後8時12分現在のHPの総アクセス数は1369631という回文数でした。1357531の回文数について4月22日の記事で取りあげたばかりですが、この1369631もなぜかしら惹き付けられるものがあります。一体何にだと思いますか?
スバリ、上4桁の1369という数字にです。1、3、6、9の数字の並び、別に等差数列や等比数列になっているわけではありませんが、何かが匂います。
ヒントです。この数、「何かの2乗になるんじゃないか?」っていう雰囲気を感じませんか?逆に言うなら、√(1369)は何でしょう。
これを確かめるのは割と簡単です。
○2=※※※9
みたいに2乗したときに1の位が9になる○の数って、1の位が3か7だけです。
202=400
302=900
402=1600
だから
○2=1369
になるとしたら
30と40の間の数しかあり得ません。
1369は3の倍数じゃないから33は違います。
では、372を試しに計算してみると、1369に一致します!
2乗になりそうなヒントを感じ取れたら、計算はたったの1回(37×37=?)だけです。
結論です。1369は37という素数の2乗でした。そういうことで、素数が好きな人にとっては、1369は何かしら惹かれる数字なんです。
それでは、1369にちなむ瞬殺クイズを2問。
① x2+74x+1369 を因数分解しなさい。
足して74、かけて1369になる2つの数を探すのは少々厄介かもしれませんが、皆さん方は難無くできるはずです。勿論、答は(x+37)2
② 直角三角形の直角をはさむ2辺は12cmと35cmです。斜辺の長さを求めなさい。
解説は不要かもしれませんが・・・、斜辺をx(cm)とすると、三平方の定理より
x=√(122+352)=√(1369)=37
よって、x=37(cm) ・・・(答)
では、1369631という数について考察してみましょう。これは素数でしょうか?私、電卓使って10分ほど心当たりある数で割ってみましたが、約数を見つけることができず、根負けしてネット上の素数判定機にかけてみました。
1369631=461×2971
461で割り切れるとか簡単に思いつくはずがありません。
ということで、1369631は2つの素数の積になる「半素数」で、その約数は、1, 461, 2971, 1369631の4個になります。
最後に、今日取り上げた1369631について、数字の並びをそのままにして、加減乗除等の記号を入れて、この数字が現れた日にちである5月6日をそのまま並べた56を作ってみます。
(-13+69)(6÷3-1)=56 → 5月6日
皆さんだったらどのような式を作りますか?
【校長】
学校のピクトグラムとして相応しいのは?
小学6年と中学3年を対象に、18日に行われた全国学力・学習状況調査(全国学力テスト)の問題が翌19日の新聞に載っていました。参加校は全ての国公立校と、約50%の私立校で、小6と中3合わせて212万人が同一日に検査を受けたと知り、センター試験の約55万人と比べいかに大規模な試験だったかと、驚きをもって記事を読んだところです。
私、中学3年生を受け入れる高校の校長として、彼らがどういう問題を解いてきたのか知っておくことは必要だと思い、全ての問題に一通り目を通しました。
やはり、初めて中3で導入された英語が印象的です。「聞く」「読む」「話す」「書く」の4技能をバランス良く身に付けて活用できるかを調べるため、自分の考えを英文で表現したり、話したりする問題など、高校入試よりも難しいのではと思いました。
英語の問題、新聞では「話す」技能の問題は省略されていましたが、テレビニュースで試験の様子が放映されたので概要を知ることができました。マイクが付いたヘッドセットを装着した生徒の声をパソコンで録音する方式で実施され、USBメモリーに保存された録音音声を委託業者に送って評価するんだそうです。サイトの個人ページにログインして動画を見ながら答えており、「なるほど、こうしてやるんだ。でも隣でしゃべっている生徒の声が聞こえてこないのかな・・・?」と心配しました。一体どんな問題が出題されたんでしょう。国立教育政策研究所のHPにはスクリプトがpdfで公開されているようですから、後ほど目を通してみようと思います。
「書く」では、世界の食糧危機と日本の食品ロス問題(毎日沢山の食糧が廃棄されている問題)のレポートを読んでどう感じたか、英文で書かせる問題がありました。限られた解答時間の中でどういった観点から書けばいいのか悩んだだろうな・・・と思いました。
でも、今回一番印象に残った問題として敢えて一つ取り上げるとすれば、次の問題です。外国人旅行客用のタウン・ガイドを作成するために、「学校」を表す2つのピクトグラム(案内用イラスト)のうち、どちらが良いかをウェブサイトで意見を募集するという設定で、1つを選んで自分の考えや理由を25字以上の英語で書くというものです。
皆さんだったらどちらを選びますか?自分がもつ「学校」のイメージで選ぶのではなく、「外国人旅行客にとって」という前提条件が問題をことさら難しくしているようにも思います。一体どちらを選んだ中学生が多かったのでしょう?
私、とても興味を持ちましたので、担任の先生の協力をいただき、機械科3年B組の生徒の皆さんにSHRの時間にアンケートを実施してもらいました。結果は、Aが22人(55%)、Bが18人(45%)で僅かにAのほうが多かったものの拮抗していました。
Aを選んだ人たちは、「黒板と本があり、大きい大人(先生)が小さい子ども(生徒)に何かを教えているようで、一目瞭然で学校をイメージしやすく、この光景は世界共通だと思う」といった理由を挙げた人が多かったです。また、「Bの建物は病院や図書館、博物館かもしれないし、日本人ならともかく、外国人にとって時計があるこういう形状の建物が果たして学校と認識できるのか?」と疑問を呈した人もいました。
一方、Bを選んだ人たちは、「Bは生徒たちが朝8時に登校しているようで学校と分かりやすいけど、Aは塾(予備校)とも捉えられるのでは」といった理由を挙げていました。その他、「Aは読み聞かせをしているようで幼稚園や保育園のようだ」とか、「外国の学校で(日本のように)教師から生徒へ一方的な授業がされているのだろうか」と、いぶかる理由を挙げた人も数名いて興味深かったです。それにしても、それらの理由を英語で書くのは、語彙力の問題もあり難しかったかもしれません。
文部科学省は中3で「英検3級相当以上」という学習目標を掲げているようです。それはともかく、自分で考え、それを英語で表現し、相手に伝える力は、私の世代の人たちが英語学習で求められた力とは大きく異なっているように思えます。
グローバル化という言葉が盛んに使われている昨今、コミュニケーション能力重視の姿勢は続くでしょうから、日頃から自分の考えを英語で伝える練習はますます必要になることでしょう。でも、一朝一夕にはそういった力は身につかないはずです。新入生の決意作文の中に、「特に、中学校のときに苦手だった英語を頑張りたい」と10名近くの生徒の皆さんが書いていましたが、そういうところを踏まえて地道な努力を期待します。
【校長】
読書の千本ノックとは?

公益財団法人読書運動推進協議会のHPには週間の意義として次のようにあります。
幼少のときから書物に親しみ、読書の喜びや楽しみを知り、ものごとを正しく判断する力をつけておくことが、子どもたちにとってどんなに大切なことか・・・。子どもに読書を勧めるだけでなく、大人にとっても子どもの読書の大切さを考えるとき、それが「こどもの読書週間」です。
いきなりですが、皆さんは月に何冊ぐらい本を読みますか?
図書館の記録によると、昨年度は一人当たり10.1冊という数字が残っていますので、割り算すると零点いくらという冊数になります。多いのか少ないのか・・・?勿論、学校の本ばかり読んでいるわけではないはずです。「朝の読書」が設定されていることもあるのかもしれませんが、司書の坂口先生や国語科の先生たちから「本校生は意外と読書家が多いのでは・・・」と伺い、嬉しく思っています。
というのも、私は趣味の欄とかに躊躇なく「読書」と書き込めるようになったのは30代になってからです。高校の頃を思い起こすに、分厚い時刻表が愛読書というほどの鉄道少年でしたから、読書の記憶は宿題で読書感想文を書くために仕方なく読んだこと以外全く思い出せない、いわゆる「不読者」でした。

その意味で、図書室に掲示してある右の写真、「不読者を0に」というキャッチフレーズが目に入ると、当時を思い出して今でもドキっとします。
ところで、平成24年6月12日の毎日新聞に掲載された「読書の千本ノック」という記事の切り抜きを手元に残していましたので、出だしを紹介します。
石川県の星陵高校に野球部名誉監督の山下智茂さんを訪ねた時のこと。「野球は人間がやるものだから、心がしっかりしてないとプレーに表れる。ところで人間性を豊かにし、精神力と忍耐力を同時に高める指導法がある。何か分かりますか?」という。
答えは「読書」。だから、野球部にいつも「本を読め」と指導する。山下さんの〝読書の千本ノック〟を、まともに受けて立った高校球児がかつていた。山下さんはこの生徒のために3カ年計画を立て、定期的に書物を手渡し続けた。最初は日本や世界の歴史書。福澤諭吉、二宮尊徳、アリストテレス…。過酷な野球練習の後も、生徒は片道1時間の電車通学を利用し、本を読み続けた。山下さんは振り返る。「彼、松井秀喜君は、僕が知る中で最も本を読んだ高校生です」
この記事を読んだ当時、私、とても驚きました。というのも、読書って読解力が鍛えられる、想像力が豊かになる、表現力が身につく、くらいの認識しかなかったからです。スポーツにも活かされる一面があったとか考えたこともありませんでした。読書は、国語の勉強などの一面だけではなく、普段の生活の中の至るところで深く関わり、意識しなくてもあらゆる面で自分を高めてくれているのかもしれません。凄いことです。
そういえば、高校の英語の授業で、A is to B what C is to D(AとBの関係はCとDの関係と同じである。【A:B=C:D】)という構文を習ったとき、次のような文に出会ったことを思い出しました。なかなか含蓄深い英文であり当時、もっともっと深くその意味を考えればよかったと今になって思います。
Reading is to the mind what food is to the body.
読書の精神に対する関係は、食物の肉体に対する関係と同じである。
10連休突入が間近です。この記事を読んだことを機会に一人でも多くの生徒の皆さんが連休中に本に親しむことを期待します。本校の図書館だけでも2万冊を越える本がありますよ!
【校長】
興味深い性質を持つ回文数
汗ばむ陽気の土日でしたが、生徒の皆さんはいかがお過ごしでしたか?
私は、昨日鹿児島市の平和リース球場で行われた第144回九州地区高等学校野球大会2回戦の応援に行きました。今年度新たに25名の新入部員を迎え、グラウンドの練習もますます熱がこもっている野球部、強豪校である福岡大学附属大濠高校相手にどのような戦いを繰り広げるのかと大変楽しみにしながら向かったところでした。
三回1死一、三塁で内野ゴロの間に1点を先制したものの五回に1点を失ってしまい、1対1のまま延長戦になりました。息詰まる投手戦を制したのは大濠で、十回表にホームランなどで一挙4点を入れられ結局1対5で敗れました。
選手の皆さん、白熱した試合を見せていただきありがとうございます。この後、RKK旗、NHK旗、夏の予選と続きます。見つかった課題を分析して捲土重来を期待します。また、第1試合で北九州の真颯(しんせい)館高校を相手に9対6で勝利し、8強入りを決めていた熊本西高校の選手の皆さんも五回まで応援をしていただきました。学校を代表してお礼を申し上げます。
写真には、飛行機雲の跡が沢山残っています。スマホのアプリ(flightradar24)で調べたところ、大阪や福岡と沖縄(那覇空港)を往復する国内線の他に、アンカレッジやバンクーバ(カナダ)、ロサンゼルス等から香港やタイペイ、シンガポール等に向かう国際線が頻繁に鹿児島上空を飛んでいることが分かりました。桜島の雄大な眺めとともに、日常と違う風景を久々に見て楽しい一日でした。
話は大きく変わりますが、昨年12月9日の記事で総アクセス数 1248421 という回文数を取りあげていました。これは初めの4項が初項1、公比2の等比数列でした。それからおよそ4ヶ月半後、またしても面白い回文数(右から読んでも左から読んでも同じになる数)が現れました。
私は夢の中でしたが、多分真夜中の午前1時20分頃に総アクセス数 1357531 を通過したはずです。これは、初めの4項が初項1、公差2の等差数列になっています。
これは素数でしょうか?
2002÷11=182のように、偶数桁の回文数は必ず11で割り切れるという興味深い性質がありますが、これは7桁で奇数桁です。ひょっとして素数かと胸が高まります。
でも違います。7で割り切れます。7の倍数の見分け方は昨年9月1日の記事で触れているとおり*ですが、3桁ずつ区切ってまとまりの和の差(1+531-357)を求めると392で、これは7の倍数(392÷7=56)になっています。ということで素因数分解すると、
1357531=7×19×59×173
従ってその約数は、1, 7, 19, 59, 133, 173, 413, 1121, 1211, 3287, 7847, 10207, 23009, 71449, 193933, 1357531の16個です。
ところで、7×173 の結果 1211 と 19×59 の結果 1121 を見て何か気付きませんか?
1357531=7×173×19×59=1211×1121
となって、なんと4桁×4桁に分解したらそれも回文数の形になっています。割と有名な事実ですが、知らなかった生徒の皆さんも多いかもしれません。いくつか例示してみます。
11×11=121 12×21=252 22×22=484
101×101=10201 102×201=20502
111×111=12321 1001×1001=1002001
1002×2001=2005002
1102×2011=2216122 2002×2002=4008004
・・・・
このように回文数は、入試に出ることはあまりないかもしれませんが、興味深い性質を持っていることが多く、趣味の数学の分野ではよく研究の対象になっています。
最後に、今日取り上げた1357531について、数字の並びをそのままにして、加減乗除等の記号を入れて、この数字が現れた日にちであり、4月22日をそのまま並べた422を作ってみます。
(-1+3!)×5!!!+7×53+1=422→4月22日

この小町算、やり始めると困ったことにポテチと一緒で「やめられない・止まらない」なんですよね、これが(..;)
【校長】
*7の倍数の見つけ方(昨年9月1日の記事より引用)
証明は省略しますが、次のように面倒です。7で割った方がよっぽど速いので7で割ることをお勧めします。
①例えば、数字を (abcdefghijkl) とします。
(<例> a=6, b=7, c=3 の場合 (abc) は 673 すなわち 六百七十三 を表します)
②この数字を、1の位から3桁ごとに分けていきます。
abc,def,ghi,jkl
③3桁の塊(かたまり)を一つ飛ばしにグループ化します。今回は色分けして赤と青のグループにします。
abc,def,ghi,jkl
④グループ毎に和を求めて、その差を計算します。 ( abc + ghi ) – ( def + jkl )
(もしも、青の和の方が 赤の和よりも大きいのであれば、青 – 赤 の計算をします)
⑤この 差 が 7の倍数であれば、もとの abcdefghijkl は7の倍数です。
<検証> 813297496970 という数字の場合
(813+496)–(297+970)
=1309 – 1267
=42
(7の倍数なので7で割り切れる。実際、813297496970÷7=16185356710)
「ノー レイン ノー レインボーって・・・」
昨日、始業式に引き続き行われた頭髪服装検査が終わって校長室に帰るとき、多くの生徒たちと一緒になりました。前を歩く生徒たちが(私に気付いていないのか?)今年度のテーマ「飛躍」に添えたサブテーマの“No rain, no rainbow. ”についてさっそく話をしていました。別に聞き耳を立てたわけではありませんのでよく聞き取れませんでしたが、ポジティブな感想を述べあっているようで嬉しく思いました。
ひょっとして英語の授業でもう習った人たちがいるかもしれません。私が高校生だった頃、「・・・すればするほど、ますます~だ」という意味の《The + 比較級 …, the + 比較級~》の構文を初めて習ったときのことです。
英文で「…」や「~」の部分が省略された“The sooner, the better.”と先生が板書され、「訳してみろ!」とおっしゃったのを鮮明に覚えています。
正解は、「早ければ早いほどよい」「早いにこしたことはない」です。今になって思えば、大げさかもしれませんが「心の琴線にふれる」とはこういうことを言うのかと考えるほど、面白い表現だと思いました。そして、先生の「これはわずか4語からなる英語で一番短い諺(ことわざ)だ!」という解説も当時の私は全く疑問を抱くことはなく、脳裏に刻み込まれました。
それから何年経ってからでしょうか?多分20~30代の頃だったと思います。サブテーマに定めた“No rain, no rainbow. ”という含蓄ありすぎる諺に出会いました。
直訳は『雨がなければ、虹はない』ですが、勿論、雨は『試練』、虹は『夢』や『希望』の象徴です。頑張らなければ結果は出ない、目的を遂げる前には苦しまないといけないなど、色々と解釈できることも知り、その奥の深さも含めていっぺんに好きな諺になりました。
と同時に、やり切れない複雑な思いで一杯にもなりました。というのも、私、英語の先生の言ったことを間に受けて、一番短い英語の諺は唯一“The sooner, the better.”とばかり信じ切っていたので、他にもあることを知って驚いたというか、了見が狭いままその歳まで生きてきたことをとても不甲斐なく思ったからです。「唯一」とか「絶対」、「一番」などという形容詞は、万人が話し常に揺れ動く言語の世界ではあり得ないということを悟ったところでした。色々調べてみたらわずか4語の諺、結構ありました。今、ぱっと思いつくだけでも次のようなものがあります。
Easy come, easy go.
直訳は「簡単に手に入るものは、簡単に出て行ってしまう」、つまり「得やすいものは失いやすい」という意味ですから、日本の諺でいう「悪銭身につかず」が近いでしょうか?
Tomorrow is another day.
「明日は別の日なんだ」、そうポジティブに諭しているように思います。「明日は明日の風が吹く」のように楽観的に訳すといいかもしれません。
Better late than never.
「遅くなってもやらないよりはましだ」と訳すことが多いようですが、待ち合わせの時間に遅れて来た場面で「遅れても来ないよりはましだ」という意味で使われているのを見たことがあります。
諺、名言、格言は長い時代を経て受け継がれてきた貴重な人生訓です。特に、英語の諺は日本語の諺にない文化的背景が感じられたり、口ずさみたくなるような語感があったりと、含蓄が深いように思います。就職試験にも出題されているのを見たことがあります!
“No rain, no rainbow. ”に出会ったのをきっかけに、皆さんもお気に入りの英語の諺を見つけて座右の銘にしてみてはいかがでしょうか。
【校長】
167名が入学しました

特に入学式では、多くの御来賓の皆様方の御臨席を賜りましたことに改めてお礼を申し上げます。
さて、本日、晴れて入学を許可された新入生は本科163名、専攻科4名の計167名です。この数字をもとに、今朝家を出るときからやってみたかったことがあります。それは、学校に着いてすぐHPを開けたときの総アクセス数で167を作る小町算をすることです。
式後にじっくりと考えてみようと、朝とりあえず数字をメモしておきました。7時24分現在の総アクセス数は、1344667でした。
この数字の並びをそのままにして、加減乗除等の記号を入れてみます。
134+46-6-7=167
偶然でしょうか?あまりにも簡単にできて拍子抜けです。ということで、もう1問挑戦します。今日4月8日の数字をそのまま並べた48を作ってみます。
1+3+44+(6-6)×7=48
こちらも簡単にできました。皆さんだったらどのような式を作りますか?
ところで、「167って何て思い出深い数字だろう・・・」と「入学許可」の時、壇上にいながら思っていました。というのも、167は私が学生の時の学籍番号で、4年間試験の答案用紙など色々な折に167を記入していたことを思い出したからです。
いつかはこんなこともありました。私が素数好きということを知った教授から不意に問題を出されたことがあります。「167の3桁の数を並び替えてできる数字のうち素数じゃないのは何~んだ?」というものです。
167は素数っぽいです。ひっくりかえした761は? 617は? 671は?
皆さんは瞬間的に動物的勘で答えることができますか?
実は、671だけが素数ではありません。671=11×61と素因数分解されます。671は11の倍数なんです。
3の倍数、4の倍数、5の倍数とかを見分けることは簡単ですが、皆さんは11の倍数を見分けることができますか?
証明は省略しますが、各位を一つ飛ばしに足した”和”の”差”が11の倍数又は0であれば、その数は11の倍数になります。
例えば、175428 を計算してみましょう。
一つ飛ばしに色を塗り分けてみますと 175428 。
そして、それぞれの和を計算します。
赤の和 1+5+2=8
青の和 7+4+8=19
19-8=11
これは11の倍数ですから、175428は11の倍数です。
先ほどの671は、(6+1)-7=0ですから、11の倍数ということです。皆さん知っていましたか?全く有名ではありませんが、知っておくと約分とかするときに使えることがあるかもしれません。
167の3ケタの数字を全部かけると42、これをひっくり返した24は風水5大吉数の1つで、金運・仕事運アップをもたらすラッキーナンバー、しかもその音「に・し」は私の名前のオノマトペ。これもなかなかいいです。
【校長】
「令和」に思う
4月1日、平成31年度がスタートしました。新着任された11名の先生方を御紹介した後、最初の職員会議を行いました。引き続き、学年会や部会、教科会などが開かれ、生徒の皆さんが年度当初スムーズに学校生活が送れるよう様々なことを協議しました。明日からは時間割の編成も始まります。
ところで、昼前に新元号が発表されました。私も固唾を飲んで事務室のテレビを見守った一人です。詩人の伊藤比呂美さんと作家の瀬戸内寂聴さんの対談で「荒波」とか出てきていたのを思い出しながら、そんなのだったらきっと面白いだろうな・・・とか思っていたら、まさかまさかの「令和」。
菅官房長官が額縁を掲げた時、「命令の『令』?、冷たい響きの語感だな」というのが第一印象でした。テレビで色々予想しているのを見て、自分なりに様々考えていましたが、ことごとく外れてしまい、正直Rで始まるとは全く予想もしてなかったので大変意外でした。後でよく考えてみたら、令には「令息」や「令嬢」のように使われ、「よい」「立派な」という意味があることを思い出しはしましたが・・・。
私、つい先日から来年1月の試験に向けて奈良検定の勉強を始めていました。昨年受けた京都検定と違って、神社仏閣や史跡、歴史、年中行事、伝統工芸の他に、万葉集と古墳が結構出題されています。万葉集の中の有名な和歌の一部分が隠されていて、そこを埋める問題(4択)です。「この歳で万葉集を勉強しないといけないのか、やっかいだな・・・」と思っていたまさにその矢先に、「令和」の出典が万葉集と知ったわけです。「何と素敵なことだ!」と驚くと同時に「勉強のし甲斐がある」と嬉しくなりました。
安倍首相の談話によると、「人々が美しく心を寄せ合う中で、文化が生まれ育つという意味が込められている」そうです。
で、出典の「初春令月 気淑風和」って一体何?
さっそく調べてみました。万葉集の梅花(うめのはな)の歌32首の序文なんだそうです。
「初春の令月にして、気淑(よ)く風和らぎ、梅は鏡前(きょうぜん)の粉(こ)を披(ひら)き、蘭は珮後(はいご)の香を薫らす」
【現代語訳:新春の好(よ)き月、空気は美しく風はやわらかに、梅は美女の鏡の前に装う白粉のごとく白く咲き、蘭は身を飾った香りの如きかおりをただよわせている:中西進氏「万葉集全訳注原文付」講談社文庫】
1300年も昔に誠に風雅なことを考えたその人に思いを馳せました。そうこうしていたら、ちょっと馴染んできたのか、「令」はキリッとして「和」は温かい感じがしてきて、響きも綺麗な言葉のようにも思えてきました。不思議です。
一週間後に迫った始業式で元号に触れない校長は皆無のはずです。色々と伝えたいことはあります。何を話そうかと今から悩んでしまいます。
【校長】
見慣れない列車が人吉駅に
学校は今日が修了式。先立って行った表彰式では皆勤・精勤賞や成績優秀賞などの校内表彰も含めてのべ493人を表彰しました。凄いことです。
生徒たちが昼前に放課になった頃、「今日の人吉駅清掃ボランティアは中止します」と校内放送が入りました。「エッ?なぜ??」と担当の先生に連絡をとったところ、「人吉駅でイベントがあっていて清掃どころじゃなさそう」ということでした。
すっかり忘れていました。今日は人吉駅にJR九州のD&S列車*が大集結する日でした。早速、1時間休みを取って駅に向かいました。黒山の人だかりです。私、人吉駅が足の踏み場もないほどこんなに賑わっているのを見たのは初めてです。図書館にあった「人吉市史」によると、昭和30年~40年代は、青井阿蘇神社の「おくんち祭り」の日だけは臨時列車が出るほど人吉駅が賑わっていたという記事を読んだことがありますが、本当に凄いことになっていました。
頂いたパンフレットには、「観光列車サミット in 人吉球磨」とありました。それによると、「『SL人吉』をはじめとするJR九州のD&S列車が3本も運転されている熊本県人吉球磨で、『観光列車と街づくり』について大人から子どもまで楽しみながら考える参加形のイベント・・・」とありました。
主催者らしい方とお話したところ、「肥薩線人吉駅に『A列車で行こう』、『いさぶろう・しんぺい』、『かわせみやませみ』、『SL人吉』、『指宿のたまて箱』、くま川鉄道の『田園シンフォニー』の6つもの観光列車が勢揃いするのは『最初で最後だろう』」ということでした。
何でも、『いさぶろう・しんぺい』号が人吉駅に到着して出発するまでの13:08~13:22までの14分間が6つの観光列車が一堂に会する奇跡の瞬間だったそうで、私も立ち会えて幸せでした。
↑左の写真(1番ホーム:A列車で行こう、2番ホーム:いさぶろう・しんぺい) 右の写真(庫1番:SL人吉、庫2番:指宿のたまて箱)
↑左の写真(3番ホーム:かわせみ やませみ、くま鉄ホーム:田園シンフォニー)
*D&S列車とは、個性溢れる外観や内装で運行され、乗ること自体も楽しんでもらうための仕掛けやイベントも用意されているJR九州の観光列車の総称(現在11種類)で、「デザイン&ストーリー」の略なんだそうです。
【校長】
自分はなぜ選ばれたんだろう・・・
いよいよ授業がある週としては今年度最後の週になりました。色々な意味で有終の美を飾るとともに、教室をピカピカにして後輩に渡せるよう5S(特に「清掃」)に力を入れてほしいと思います。
話は変わりますが、司書の坂口先生が、この3月末日をもって廃校になる多良木高校の図書館から75冊の本を貰って来られました。図書館だより第9号(2月27日発行)に「保管転換一覧」として紹介されているとおりです。管理上必要と認められる物品や資料を他の機関に移したり、管理区分を換えたりすることを行政では「保管転換」という難しい言葉を使いますが、その作業をされたわけです。
廃校になる学校に残された図書は、引き取り手がなければ廃棄処分にされるわけですから、選ばれた本たちは本校の図書館で再び日の目を見ることになりきっと喜んでいることでしょう。
私も早々にその図書が集められたコーナを見に行き、どのような観点から選書をされたのか説明を受けました。背表紙を眺めていたら、本たちのつぶやきが聞こえてきそうでした。「自分はなぜ選ばれたんだろう・・・?」と。
そんなことを考えていたら、私自身も最近、終活とか断捨離とか称して一気に本を捨てることがあるわけですが、どうしても捨てきれない本が本棚に残ることがあり、その本たちの気持ちと通じるところがあるのでは・・・?とか思えてきました。
多良木高校図書館にあったどのような本に光が当たり、息を吹き返したのか、どうして自分は選ばれたんだろうと思っているのか、それらの答えを想像しながら本の筆者と言葉を交わしてみるのも「小さな幸せ」かもしれません。図書館に足を運んでみませんか。
なお、本だけでなく家庭科で使う調理道具やアイロン台、皆さん方の机・椅子、視聴覚室用の長机、野球部用の防球ネット等も貰ってきてあることを申し添えます。
【校長】
1326635 → アインシュタイン博士の誕生日
今現在、午前8時16分現在の総アクセス数は1326635
数字の並びをそのままにして、加減乗除等の記号を入れてみたくなりました。
13+266+35=314 → 3月14日(アインシュタイン博士の誕生日)
色々やっていたら苦しいですが、こんな式もできました。
132+6!!!!×6!!!!+3!-5=314
ところで、今日3月14日はホワイトデーですが、「円周率の日」でもあります。円周率については、昨年の今日、思いを綴りました。
こちら → 円周率の中の「31415926535」
そして、日本パイ協会が円周率のπにちなんで「パイの日」、日本数学検定協会が「数学の日」と定めているようです。
さらに、E=mc2の方程式で有名なアインシュタイン博士の誕生日(1879年3月14日~1955年4月18日)なんだそうです。
アインシュタイン博士といえば、ベロをだした写真(ネット上に溢れている写真をここにコピペすることが著作権上どうなのか不明ですから見合わせます)がとても印象的で、名前くらいならだれでも聞いたことがあるはずです。
ドイツの物理学者でいわゆる相対性理論を発表しためっちゃくちゃ凄い人で、自然科学の分野ではニュートンと双璧をなす人類史上希な天才などと言われています。伝記によると、幼いころから数学に関しては才能を発揮していたそうで、9歳の時にピタゴラスの定理の存在を知り、その証明を寝食を忘れて考えたとか、12歳で微分積分学を独学で学んだとかあります。
親日家であり、戦前の大正11(1922)年、講演のために40日間に渡って来日し、行く先々で「アインシュタイン万歳!」と数千人の群衆が目に涙を浮かべながら熱狂的に迎えたと記録にあります。当時の日本人の「外国の学者に対する尊敬の念」を窺い知ることができます。
ところで、先述したE=mc2 (エネルギー=質量 X 光速の2乗)、これは特殊相対性理論から導き出されたもので、エネルギーと質量が等価関係を持ち、相互に互換性があり、条件が整えばエネルギーが質量に変換されるのと同様に、質量もまた適切な条件のもとではエネルギーに変換されることを示しています。この方程式により人類は「原子の火」を手に入れて、まず原爆が次いで、原子力エネルギーが生み出されました。世界で最も有名な科学方程式と言われるこの式、物理基礎でもちらっと学習するかもしれません。
この式の偉大さを中学生の皆さんにも分かりやすく言えば、そこらへんに落ちているただの石ころが、エネルギーの固まりだと言っている点が凄いのです。なぜならc=光速、光の速度を言うのはものすごく速いので、これの2乗をかけるととんでもないことになります。なんでも、広島の原爆でエネルギーに変わった質量はたったの1gだったそうです。ということで、物質のもっているエネルギーの量がものすごく莫大であることを示した式と言ってもいいです。
エネルギーと物質の質量の関係がこんなに簡単な式で表されるということに改めて驚かされます。
実際、質量1[ k g] を手元の電卓でエネルギーに変換してみます。光速度 c= 299792458[m/s]ですから、次のようになります。8.9875517873681764×1016[J]([J]はエネルギーの単位)
アインシュタインはこの公式を純粋に理論から導きだしたので、核分裂によるエネルギーの解放などは予想もしていなかったと言われています。

連合軍の占領下、「原爆」という文字が使用できなかった当時の事情らしいです。
【校長】
東大入試をリードする就職試験
学校は6日・7日の高校入試に引き続き8日はその採点日、9日・10日の土日と続きますから、生徒の皆さんにとっては5日連続の休みになっています。充実した家庭学習ができていますか?
今朝、ある生徒が登校してきていました。勿論、制服姿です。校内に人っ子一人いないことに気付いたのか、怪訝そうな表情を浮かべているのに偶然出くわしました。「今日は家庭学習だけど・・・」と声をかけたところ、「マジッすか?!」と言ってばつが悪そうに、でもどことなく嬉しそうに帰って行きました。ちょっとだけ可笑しかったです。
話を大きく変えます。以下は昨年12月19日にアップした「平成30年度の就職試験を振り返る」という記事の冒頭です。
就職試験問題を分析した結果、発想力や説得力を問う面白い問題を出題する企業が増えているな・・・という思いで綴っていました。
そしたら、何と2月26日に実施された東京大学の入試(英語)でまさに次のような問題が出題されていました。
本校生が受けた就職試験のほうが、大学入試より先を行っていて驚きです。でも実に楽しい問題と思いませんか?全世界でもいいとか、夢があり過ぎです。
某予備校が作成した模範解答に添えてあったポイントには次のようにありました。
その祝日の意義は何か。また、なぜそのような祝日が望ましいと考えるのか。存在意義、存在理由を論理的に述べて「ああ、そんな祝日ならいいね!」と採点者を説得することが必要。ただし、自分が知っている表現で題意を満たせる祝日を発想できるかが焦点となり、語数が60~80語とやや長めなこともあり、かなりの難問。
確かに英語では難しいかもしれませんが、「日本語」でならどんどん浮かんできそうです。生徒の皆さんも早めの就職試験対策として、まずは日本語で考えをまとめてみませんか?
【校長】
入試の朝、レンゲソウを見つけました

教務部で入試の係をしていた頃、受験生が帰った後の教室の整備をしていて、机の上に残された大量の消しゴムの屑に答案用紙との格闘の跡が偲ばれました。
これまで培ってきた力を余すところなく答案用紙にぶつけてください。
ところで今日3月6日、受験生の皆さんにとっては朝からあいにくの肌寒い雨模様になりましたが、虫たちが冬眠から目覚め活動を始める頃を意味する啓蟄(けいちつ)です。
啓蟄を含む二十四節気は太陽の黄経によって日が決まり、年によって変化します。私、3月5日前後と記憶していました。後で触れますが、今朝、通勤中に今年初めて目にしたレンゲソウ(蓮華草)に春を感じ、2019年の啓蟄はいつかな?って、とても気になりました。学校に着いてすぐネットで調べたところ、何と、今日3月6日でした!
予感が当たり、とても嬉しくなりました。ということで、朝から本校のホームページを開けたときの総アクセス数だった1320576という数字の並びをそのままにして、加減乗除等の記号を入れて、記念すべき今日の日にち3月6日の数字をそのまま並べた36を作る小町算に挑戦してみます。
弥生3月も早くも6日ということで、6通り作ってみます。
1-3+20+5+7+6=36
1+32+0!+(5+7)÷6=36
1-3+2-0!-5+7×6=36
(1+3+2)×(0+5+7-6)=36
1+3+2+0!+5×7-6=36
(1+3+2+0){(5+7)÷6}=36

私が小学生の頃の話です。肥料にするためと聞いていましたが、秋にレンゲソウの種を田んぼに播き、春に咲かせて、耕運機ですきこんで (土でならして)いたのをよく目にしていました。そんな「れんげ農法」が盛んだった当時は、春になると田んぼ一面が赤紫に染まっていたものです。「日本の原風景」とか持ち出すと、ちょっと大袈裟かもしれませんが・・・
そんな風景、最近あまり見かけないな、と思っていたら、去年の4月中旬でした。くま川鉄道で湯前に向かっていたところ、あさぎり駅の前後でレンゲ畑が沢山残っていているのを車窓越しに見てとても懐かしくなりました。
生徒の皆さんは、レンゲソウで首飾りとか作って遊んだ経験がある人はいますか?私、何かの拍子に近所の子からレンゲソウの首飾りのプレゼントを貰ったことがあります。丁度50年前の1968年、グループサウンズが一世を風靡して、ザ・タイガーズの「花の首飾り」が流行っていた頃のメルヘンチックな思い出です。
その曲で歌い込まれているのは、「ひな菊」の首飾りです。色々な歌手がカバーしているので、耳にしたことがある人も多いことでしょう。
【校長】
恋しい休憩時間!?
昨日実施した「親と子で学ぶ管内事業所説明会」、いかがでしたか?
進路指導部の松村先生から「会の前後で皆さん達の顔つきや表情が変わって見えた」という感想を聞いて嬉しく思いました。
冒頭の挨拶でも申し上げたとおり、今年度の2年生のインターンシップでは、本田技研工業様、井関熊本様、JNC様など7社にお世話になり、初めて人吉球磨管外の事業所で就業体験を実施しました。先日、その成果と課題をまとめた報告書を教育委員会に提出しましたが、添えてあった感想文を読んで「エッ!?」と思う表現を見つけました。それは・・・
ずっと立ち作業で足が棒のようになり、休憩時間がとても恋しかったです。
というものです。「休憩時間が恋しい」とは、現場で働いてみて初めて実感する素直な感想です。同時に、とても面白い表現だとも思いました。
「恋しい」は、「あなたが恋しい」(I miss you.)のように人に対して使うのが最も自然な感じがするわけですが、考えてみれば「異国の地から恋しい日本に思いを馳せる」とか「こたつが恋しい季節になりました」のようにモノを対象としても使えるんですよね。
「恋」で思い出すことがあります。
百人一首を全部覚えるのが宿題になった頃ですから、高校1年の冬休みだったと思います。課題考査で出題されるということもあり、割と本気に覚えていました。しかし、「恋の歌」が何と43首もあるんですよね。意味まで真剣にやっていたら、食傷気味になりました。そこで気分転換です。色々な教科に出てくる言葉(教科書の太字程度)にかたっぱしから「恋の」をつけてみて、しっくりする言葉が多いのはどの教科か考えてみました。
国語→恋の掛詞、恋の係り結びの法則、恋の丁寧語、恋の五段活用・・・
数学→恋の三角関数、恋の漸近線、恋の積分、恋の分配法則・・・
理科→恋の反発係数、恋の断熱膨張、恋の相対速度、恋のミトコンドリア・・・
社会→恋のスエズ運河、恋の暫定予算、恋の薩長同盟、恋の独立戦争・・・
今思えば、本当にしょうもないことを考えたわけですが、でもやってみると意外にロマンチックが止まらないものです。「恋は理系の用語と一番相性がいい」というのが当時の結論でした。
実際、「恋の三角関数☆」という初音ミクさん(バーチャルアイドル)の歌がありましたし、「恋の漸近線」と聞けば、時間が経てば経つほどお互いの距離は縮まるのに、どう頑張ってもくっつけない2人を想像できます。「恋の積分」というのも味わい深いです。ちなみに、
「恋」を時間で積分すると【 ① 】、さらに【 ① 】を積分すると【 ② 】
空欄、それぞれ何になると思いますか?
2年生の皆さんは、この前終わったばかりの学年末考査(数学)の試験範囲が積分でしたので是非考えてみてください。
難しく考える必要はありません。物理基礎で「加速度」を時間で積分したら「速度」、「速度」を積分したら「変位(位置)」になると習ったかもしれません。そのノリで気軽に考えると楽しめます。
私は【 ① 】は「愛」、【 ② 】には「憎しみ」が入るとすっきりします。
そう言えば、「恋を積分すると愛」という鳥人間コンテストに参加する大学生のサークルを舞台にした、どこかとんちんかんで噛み合わない恋の物語を描いた小説(角川文庫)がありました。(本校の図書館にはないそうです)
「愛を積分すれば憎しみ」については考えることがあります。憎しみは、英語でhate。そこで思い出すのがhate speech*です。生徒の皆さんもテレビ等で見たことがあると思います。特定の個人や集団を貶めて、暴力や差別を煽るような主張をするあの凄いエネルギー、一体どこから来ているのか考えたことありますか?私にはよく分からないところがあります。
でも、憎しみは、夫婦や家族など関係性が強ければ強いほど、ちょっとした諍(いさか)いをきっかけに愛が一転して憎しみに変わることがあることを考えると、生と死が表裏一体のように、愛も憎しみも根本は同じエネルギーということでしょうか?
「愛の反対は憎しみではなくて無関心」というのはマザーテレサの言葉(「出典マニア」の人達には異論もあります)と聞いたことがあります。「愛」と「憎しみ」と「無関心」の関係、考えれば考えるほど分からなくなるし、ちょっと怖い感じもしてきます。
【校長】
*ヘイトスピーチは、ウィキペディアによると、「主に人種、国籍、思想、性別、障害、職業、外見など、個人や集団が抱える欠点と思われるものを誹謗・中傷、貶す、差別するなどし、さらには他人をそのように扇動する発言(書き込み)を指すとされ、インターネットにおける書き込みもスピーチに含む」とあります。現代社会が抱える闇の部分かもしれません。
胸がざわつく17歳
今日2月22日は、「ニャン(2)ニャン(2)ニャン(2)」の語呂合わせから、「猫の日」に制定されていると朝のニュースで報じていました。この日をきかっけに、2月は全国各地で猫にちなんだイベントが開催されて、猫好きにはたまらない月なんだとか。
考えてみれば、月日をその順に並べた時、同じ数が3つ連続するのは1月11日の111と2月22日の222の2つだけです。万一、333とかあったら超気持ち悪いよな・・・とか考えていたら、今日は総アクセスカウンターに、2が沢山出現するということに気付きました。1312222という数字です。
午前7時頃からカウンターを見守っていました。多分、7時18分頃通過したはずです。
さっそく1312222で今日の日付の222を作ってみることにします。
1-3+1×2+222=222 → 2月22日
(13+1)×222÷2=222 → 2月22日
どちらも下4桁の2222を使っただけの面白みに欠ける式で、「小町算を舐めているのか!」と叱られるかもしれません。
気を取り直して、今日が誕生日の本校生が何人いるのか、名簿に検索をかけてみました。561人在籍しているから確率的に1人以上は期待できます。
1人いました。今日17歳を迎えた方、おめでとうございます。何か特別な感慨がありますか?
我が国も3年後の2022年4月から、成人年齢が20歳から18歳に引き下げられることが決まっています。その頃には、大人になる寸前の17歳という年齢は、今の19歳以上に輝きを増しているのかもしれません。
ところで、2年生の大半は既に17歳のはずです。今、その真っ最中を主人公として過ごしている皆さん方には、実感があまりないかもしれませんが、17歳というのは大人が昔を振り返ったとき印象深く刻まれている年齢だと思います。映画や文学など様々な作品でも17歳というのはよく取り上げられていていますし、大阪経済大学は「17歳からのメッセージ」という随筆コンクールを主催しています。Seventeenという女性向けのファッション雑誌もありますよね。
48年も前の話になりますが、南沙織さんというアイドル歌手のデビュー曲は「17才」*でした。私、この曲を希に耳にすると、自身が17歳のころ、どんな景色を見ていたんだろうと胸がざわつきます。(でも、残念なことに先日、2月7日の記事で取り上げた「ワンちゃん事件」以外あまり思い出せません)
大人と子どもの間で揺れる曖昧な時である17歳、きっと皆さんもずっと後になってからそのキラキラに気づくのかもしれません。
自分はどういう人間なのか、大人になるとはどういうことか、どのような大人になりたいのか、将来どんな仕事をしてどんな働き方をしているのか・・・そんなことに想いを巡らして17歳の今の自分の考えを文章にまとめておくのも有意義なことかもしれません。
【校長】
*南沙織さん、昭和46(1971)年に、この曲でデビューして1ヶ月後に17歳になったそうです。当時、テレビやラジオからやたらに流れていました。年末に日本レコード大賞(新人賞)を受賞して、紅白歌合戦の紅組トップバッターだったこと、私は小学5年生でしたが、「歌謡曲大好き少年」でしたからよく覚えています。
軽やかなメロディーも詞もどちらも好きでしたが、今にして思えば「17才」という言葉が歌詞の中に出て来ない不思議な曲だと思います。ウィキペディアによると、作詞家の有馬三恵子さんが作詞したのは既に40歳前後だったため、この曲がヒットしたときは周りから「40歳になってよくあのような詞が書けたね」と、半分呆れられるかように誉められたとあります。心温まるいいコメントです。それほど詞の内容が当時としては鮮烈だということだと思います。
小学生の私には、高校生のお姉さんの恋愛事情は眩しすぎましたが、しっかり感情移入して口ずさんでいました。ませガキだったんだと思います。多分。
その後、色々な歌手がカバーしていますので、きっと皆さんも聞いたことがあるはずです。
こめかみには夕日のうず
学校は昨日から学年末考査が始まりました。1年を締めくくる大事な試験です。全力を尽くしてください。
ところで、先日の3連休、寒い日々が続きました。生徒の皆さんは勿論、試験勉強に明け暮れていたはずですが、私は10日(日)に今年初めて金峰山(熊本市:665m)に登りました。南区島町の自宅から熊本西高校の横を通り過ぎて、河内町の手前から右折するコースで、片道17km位です。下山中の午後6時頃、雲仙普賢岳の横、島原半島に夕日が沈んでいました。あまりにも綺麗だったのでスマホでパシャリ。
夕暮れは、古来詩情をかき立てるようです。百人一首には収められてないけど「三夕(さんせき)の歌」と呼ばれる名歌があると昔、カルタ部の指導をしていた時、何かの本で読んだことがあります。さっそく調べ直すと・・・
さびしさは その色としも なかりけり 真木立つ山の 秋の夕暮れ (寂蓮)
心なき 身にもあはれは 知られけり 鴫立つ沢の 秋の夕暮れ (西行)
見渡せば 花も紅葉も なかりけり 浦の苫屋の 秋の夕暮れ (藤原定家)
いずれも新古今和歌集に採られた歌で、三句目を「けり」(詠嘆)で切り、五句目を「秋の夕暮れ」(体言止め)で結んでいます。最初の寂蓮法師の歌は意味がちょっと取りにくいですが、下2つは口語訳がなくても、今を生きる私たちにも寂寥とした景色が思い浮かんでくるほど分かりやすいはずです。秋の夕暮れの美しさと侘しさを愛でる心は日本人のDNAなのか、今も昔も変わらないと言ってもいいかもしれません。
とは言っても、夕暮れの捉え方も色々あるようでビックリです。「理系の人々」という理系へのイメージや偏見を面白おかしく描いたコミック本があります。本校の図書館には収蔵してありませんが、映画化もされているぐらいですから読んだ方がきっといるはずです。その中に「夕日」を巡って、太陽が沈むと、太陽光が通る大気の長さが長くなり、その結果、可視光線の青以外にも波長の短いその他の色も散乱してしまい、最終的に最も波長の長い赤色が目に飛び込んでくるという当然の現象が起こるだけで、なぜ文系の人たちがそんなに心を動かされるのかよく分からない・・・といった自虐?ネタで展開するストーリーがありました。私も理系の端くれのつもりですが、そこまで醒めた目で夕日を眺める人たちがいるとは…、いやはやです。
やはり、秋の夕暮れに真っ赤な太陽が沈んでゆくのを眺めながら、その瞬間に自分の二度と反復できない生の一回性に深く思いを致すだろうし、もしその隣に大切な人がいなかったら写メを送ってでもその光景を享有したいという気持ちがわき上がる(これらが文系の人たちの一般的な思考パターンなのかよくわかりませんが)のは当然だと思うし、どちらかというと私はそういうタイプです。
と言うことで、私にとって夕暮れは、中森明菜さんの名曲「トワイライト~夕暮れ便り~」が条件反射です。夕日を見るたびにタイトルに記したイントロ部を口ずさんでいた昔もありました。
私と同年代の方にとっては多分懐かしく思い出すであろうこの曲、大学を出て大阪の民間企業に就職した翌年、1983(昭和58)年にヒットしたもので、作詞が来生(きすぎ)えつこさん、作曲が来生たかおさんの姉弟による作品です。生徒の皆さん達にとっては、生まれる前の話ですから知らない人が多いかも?ぜひyoutubeなどで聴いてみてください。以下の話を納得してもらえるはずです。
「三夕の歌」のついでに、なぜこの曲について触れようと思ったかというと、昨夜、学校から帰ってラジオをかけて寛いでいたら、バレンタイン特集を締めくくる最後の曲として流れてきたからです。本当に久々に聴きました。私、懐かしさで思わず、読みかけの本を落っことしてしまいそうでした。
『や~はり あ~なたと 一緒に居たい 一言かきあぐね ・・・・・ 感じますか 届きますか この黄昏と恋便りまでも♪』
私は以前から、山口百恵さんの「いい日旅立ち」など、静かに愛する人のことを思いつめるバラード系が大好きでした。この「トワイライト」もその一つです。twilightとは、本来、黄昏(たそがれ)時、日の出前や日没後の薄明かりを意味します。初めて聞いた時、曲想自体もしみじみとして涙が出そうになったのですが、詞に対して何と素敵なタイトルをつけたんだろう思いました。でも、印刷された詞だけ読んでも、どうって事ありません。「好きな人に自分の想いを届けるために手紙を書く」、ただそれだけのことを綿々と大げさに表現しているだけです。しかし、曲が詞とあいまって盛り上がる、この効果は絶妙です。また、「一筆書く、手紙を書き送る」を英熟語でdrop a line と表記することがすんなりと腑に落ちる曲でもあります。
きっとこの曲の主人公は、恋も失恋も色々経験して、一人でいる時に美しい景色を見て、好きな人に思いを馳せることを何度もしたのかもしれません。一言一言がグッと胸に突き刺さるだけでなく、海辺の清涼感と黄昏の残照も感じさせる抒情的な名曲だと思います。もし、西行や定家が生きていたら、この曲をどう評するのか興味深いところです。
話は大きく変わりますが、若い頃の私にとって、中森明菜さんはリリースする曲ごとに「ウ~ん」「エッ!」と、思いが交錯した不思議な歌手でもありました。
デビュー曲「スローモーション」、来生姉弟の曲です。思春期のときめきを感じさせる清純なイメージ。その可愛らしさを打ち砕く「少女A」。これって不良賛歌?騙された!と思う間も無く、またしても来生姉弟の手による「セカンドラブ」。私の十八番。切ない系のバラードでやっぱり根はいい子だったんだ、とか思っていたら「二分の一の神話」で「いい加減にして〜!」と絶唱。これって突っ張りそのもの?そして「トワイライト~夕暮れ便り~」でしみじみと。どれが本当の明菜さんなのか、本校生の中にもこういう二面性を巧みに演じ分けることができる人がいるのでしょうか?
最後に・・・、かつて大阪と札幌を結ぶ「トワイライト・エクスプレス」というJR西日本が運行していた寝台特急列車がありました。出発時の夕暮れと到着時の明け方のそれぞれの時の薄明かりのイメージが命名の由来と聞いていましたが、実際に乗車して、日本海に沈む夕日などを車窓越しに眺めて納得しました。大阪駅を出発してすぐの車内放送の出だしにかかる音楽が山口百恵さんの「いい日旅立ち」で、いやがうえでも旅情が高まり、そういう意味で凝った演出をしていた列車でした。
もう一つ。明菜さんは私より6つ年下のはずだから今は何歳なんだろうかと指を折ったりもします。心の中では80年代のアイドルのまま(そういう意味ではこの記事の中で「明菜さん」は「明菜ちゃん」と表記したかった)です。でも、みんな平等に1年に1つずつ歳をとります。トワイライト(twilight)には、人生の黄昏即ち終末期の意味もあります。本を落っことすほど反応してしまったのは、心だけは若者のつもりでも、そ~っと人生の晩年が忍び寄ってきている証拠かもしれません。
【校長】
The 45th memorial day of the school piano
本日2月14日は、本校体育館にあるグランドピアノの45回目のアニバーサリーです。昭和49年(1974年)の今日、学校に設置されたと備品台帳に記録されていました。当時の価格で41,9700円。ネットで調べたところ、当時の高卒の初任給の平均(製造職)が約24,000円位、現在が約16,2000円ですから7倍弱、それを目安に現在の価格に換算してみると300万円位になります。グランドピアノを42万円で買い求めることは、今なら中古でもできませんが、こうして物価の違いを考慮すると、きっと中古ではなくて新品だったのでしょう。
本校を6年前に御退職になった江嶋先生に電話でお尋ねしたところ、校歌の作曲者でもある電気科の塩田靖弘先生が御在職中は、先生の御指導の下、生徒の伴奏で卒業式や入学式があっていたそうです。しかし、平成4年(1992年)に先生が御退職になった後は弾く生徒がおらず、体育館のステージの片隅で部活生のジャージ置き場として使われていたようです(園田先生談)。以来、多分ボールがぶつかるなど、ピアノにとっては苦難の日が続いたのかもしれません(涙)。先日点検したところ、鍵盤が上に戻ってこないなど不具合が沢山見つかり、急遽、修理と調律を行いました。
なぜ26年ぶりにピアノを長い眠りから起こしたかというと、(既に耳にしている人がいるかもしれませんが)今度の卒業式の式歌(君が代・校歌・蛍の光、仰げば尊し)は、なまのピアノ伴奏のもとで歌ってもらうことにしたからです。「伴奏してもいいですよ」と申し出てくれたのは、電気科1年の日下部(くさかべ)快生君と建築科1年の谷口純美さんです。
2人には、写真のようにボール等が当たらないようにバリアでしっかり囲ったピアノで、昼休みと放課後の少しの間、練習をしてもらっています。歌はみんなで歌いますが、伴奏は1人です。緊張のあまりミスタッチをしたとしても止まらずに歌に合わせて弾き続けることや、万一止まったとしても途中からでも(どこからでも)弾き始める力が要求されます。その意味で伴奏者には演奏技量は勿論、襷を繋ぎ続けていく駅伝選手と同じくらい強靱なメンタルが求められます。卒業式当日、素晴らしい伴奏で卒業生・在校生みんなと校歌等を高らかに歌えるよう練習を頑張ってください。
バレー部やバスケットボール部等、体育館内で練習している部活動の皆さんには、少々お邪魔になるかもしれませんが、御理解をお願いします。
【校長】
祝 総アクセス数 130万件達成
いつも本校のHPにお越しいただき、ありがとうございます。
1月に県立学校のHPシステムの更新が行われ、それ以降なぜかアクセスカウンターが伸び悩むという現象が続いています。
実際、今年度4月からの月別の1日当たりのアクセス数をグラフ化してみると、下のように推移しており、一目瞭然です。1月は12月に比べて半減してしまいました。
高速道路を走る大型トラックには、速度抑制装置(スピードリミッター)の装着が義務づけられて事実上90キロ以上出せないようになっているそうですが、いつの間にかアクセスカウンターにそのような抑制装置が付けられたのか(勿論そんなことはないはずですが)、まるで鉛が付いているかのように鈍い動きにそんなことさえ思ってしまいます。スランプは誰にでも突然訪れることと同じなのかもしれませんが・・・。
ということで、12月のペースなら1月の中旬にとっくに実現していたであろう130万件、やっと達成です。

130万! 久々にきりのいい数字です。
こういう綺麗な数字を見ると無性に素因数分解をしてみたくなります。早々、やってみます。
1300000=25×55×13
従って、その約数は、
1, 2, 4, 5, 8, 10, 13, 16, 20, 25, 26, 32, 40, 50, 52, 65, 80, 100, 104, 125, 130, 160, 200, 208, 250, 260, 325, 400, 416, 500, 520, 625, 650, 800, 1000, 1040, 1250, 1300, 1625, 2000, 2080, 2500, 2600, 3125, 3250, 4000, 5000, 5200, 6250, 6500, 8125, 10000, 10400, 12500, 13000, 16250, 20000, 25000, 26000, 32500, 40625, 50000, 52000, 65000, 81250, 100000, 130000, 162500, 260000, 325000, 650000, 1300000
の72個あることになります。
一桁目が5で終わる奇数の約数が全部で10個(約14%)ありますが、どれも「当然、あり得るよね」という約数ばかりで、以前、888888が77や777を約数に持つことに気付いた時に味わったような高揚感はありません。
では、いつものように 1300000 という数字の並びをそのままにして、加減乗除等の記号を入れて、今日の日にち2月7日の数字をそのまま並べた27を作ることに挑戦してみます。
13×(0!+0!)+0!+0!-0!=27 → 2月7日
1+30-(0!+0!)×(0!+0!)=27 → 2月7日
今回は、0!=1という定義(決め事)を使って簡単に2つできあがりました。
最後に・・・、生徒の皆さんは130万と聞いて、何か思い浮かぶことがありますか?
もし、お父さんが会社員、お母さんがパートで月10万円前後を稼いでいるご家庭だったら、130万という数字はお茶の間で時々話題になっているはずです。いわゆる「130万円の壁」です。税金や社会保険料の支払いで損しないためにも注意しておかないといけない数になりますが、まだまだ皆さんには早いかもしれませんね。気になる人は調べてみてくだい。なぜこういう制度があるのか知るところから、社会の仕組みが見えてくるかも?
【校長】
仮定法の思い出
トランプ大統領の5日の一般教書演説、いまだにメキシコ国境に壁を建設する公約の実現に強い意欲を示していることなどがテレビ等で盛んに報じられ、生徒の皆さんもきっと耳にしているはずです。
今朝7日の朝刊各紙にはその和訳が載っていました。讀賣新聞には、演説のポイント部分について英文が載っていたので、何気に目を落としてみました。
If I had not been elected President of the United States, we would right now, in my opinion, be in a major war with North Korea.
私が米国の大統領に選ばれていなかったら、私の意見では、今まさに、北朝鮮と大規模戦争になっていただろう。
たまたま読んだ大統領の英文、仮定法でした。「英語中級者の壁」とも言われるこの構文、私も高校の頃、散々苦労したことを思い出します。
手元のシラバスによると、本校では3年生の「コミュニケーションⅡ」で3学期に仮定法過去や仮定法過去完了について学習するようです。誰が名付けたんでしょう。名前がいかめしいですよね!「仮定法過去完了」って。この大統領の英文、まさにその「仮定法過去完了」かと思いきや、if節が仮定法過去完了、主節が仮定法過去という高校生泣かせのあの恐ろしい構文でした。
私が仮定法について学んだのは高校2年生の頃です。「英語では仮定の話をするとき、なぜ一つ前の時制を使うのか」、多分そんなことだっただろうと思い出すのですが、先生が熱心に説明していました。
その時、私は教室の廊下側の一番前の席で、開けっぱなしのドア越しに廊下の向こうから校舎に迷い込んだ仔犬がこっちに来るのが見えました。私と目が合うと突然立ち止まったので、「どこから来たの、お腹すいたの・・・?」とか口パクでしゃべってしまいました。当然、先生に見つかってしまい、「授業に集中してない!」とこっぴどく叱られ、怒り狂った先生が何とそのワンちゃんの首根っこを掴んで校庭に追い出してしまいました。私にとって仮定法はそんな苦い思い出と一緒に甦る構文でもあります。
そういうことを思い出しながら、今一度大統領の英文と和訳を読んでみたら、エッ?和訳がひょっとして間違っているのでは?と気付きました。
讀賣といえば、日本を代表する大新聞です。校閲はしっかりしてあるはずで、そんなことはまずあり得ないはずですが・・・。でも、right now が挿入され、「今まさに」とあるわけですから、当然文末は現在形で訳し、次のようになるべきではないかと思います。どうなんでしょう。生徒の皆さんはどう思いますか?
私が米国の大統領に選ばれていなかったら、私の意見では、今まさに、北朝鮮と大規模戦争になっているだろう。
【校長】
大きく変わりつつある高校入試
ここで述べることは1月21日にアップした「大学入試が変わる」と関連があるというか、その続編になることを最初にお断りしておきます。
私、教師になって以来、本校生は一体どういう問題を解いて入学してくるのかという観点から、高校入試の問題を毎年、結構時間をかけて眺めています。そして「最近、変わってきているな・・・」とつくづく思っていることが3つあります。
1つ目です。統計を取って分析しているわけでは勿論ありませんが、「平清盛は中国の( )との貿易に力を入れた」というような単なる知識・理解を問う穴埋め問題に代わって、記述式で「思考力・判断力・表現力」を問う問題が年々増加傾向にあることを実感しています。その記述量自体も増えているのは間違いないはずです。例えば、昨年度の社会科の問題では記述式が8問出題され、新聞に掲載された正解例に示された文字数の合計は、句読点まで含めて208文字にのぼります。過去数年分の5教科の総記述文字数は、一体どう推移しているのかグラフ化してみると、きっと顕著な傾向が見えるはずだと睨んでいます。
昔から証明が定番の数学は勿論のこと、国語や英語だけでなく、最近では理科や社会科でも、因果関係を説明させるものや、資料やグラフ・図表などを読み取って記述させる問題などが盛んに出題されています。しかも、解答を引き出すまでに読まなければならない資料や問題文がとにかく長くて多く、短時間に的確に自分の考えをまとめるためには相当な思考力や表現力が問われます。日頃から授業に主体的に臨んでおくことは勿論、様々なジャンルの本や新聞等を読んで自分の見識を深め、社会の動きにも関心を持っておくことが必要だと痛感します。
2つ目は、1つ目で述べた「思考力・判断力・表現力」を問う記述式の問題が多く出題されるようになっていることから当然言えることですが、難化傾向にあるということです。
私は専門が機械ということもあり、数学と中学生の頃から苦手だった「月」の問題を除いた理科だけは毎年全ての問題に挑戦しています。数学で例年出題されている二次関数と一次関数を組み合わせた問題や図形の融合問題(B問題)の中には、片手間では解けず、自宅に持ち帰って考え込むような問題がこのところ必ず1問はあります。誰がこんな難しい問題を作ったんだろう、この問題が時間内に解ける受験生がいるんだろうか、ひょっとして宇宙人?と思うほどです。そういう超優秀な頭脳の持ち主を早期に把握して、次のステップに向けて入学後の指導計画を立てるというのも高校にとっての難問の役割なのかもしれませんが・・・。
3つ目は、設問の中で「会話形式」で進めていくパターンが著しく増えているということです。「対話」の強調は、「主体的・対話的で深い学び」を求める次期学習指導要領を貫くキィ・コンセプトでもあるわけですが、具体的には、初めにある事象や実験が示され、これに対して数人が話し合いを進め、考察し、その過程の中に問題を組み込むパターンです。
例えば、昨年度の理科の問題では、由香さんと卓也君の会話が次のように出題されていました。
由香:・・・・の河原で安山岩が見えたのはなぜかしら。
卓也:・・・・を考えるとわかるかもしれないよ。・・・・・も興味深いね。
由香:・・・・についても、もっとくわしく調べたいね。
「~かしら」って女性語?かなり無理をして作問したようで、思わず「かわいいな・・・♪」とニヤケてしまったのは私一人ではないはずです。(「俺は・・・」で始まる会話はついぞ見たことがありません)
それはさておき、この手の問題は私たち教師に、「子どもたちに考えさせる授業をしていますか?」というメッセージを投げかけているように思えてなりません。
昨年度の社会科では、授業の一場面を扱った会話を元にした問題が出題されました。それをよく読んでみると、「先生」は何も知識を与えていません。ただ話題を提供して、答がある方向に誘導しているだけです。少々知識のある大人であれば、子どもに解き方を見せたり、答を与えたりすることは簡単です。しかし、そんなやり方ではダメだと言っているようにも思えます。
中国には、「飢えている人に魚を与えると喜ばれるが、その場しのぎにしかならない。それよりも魚の釣り方を教えてあげることがその人のためにはなる」といった趣旨の老子の言葉に由来する格言があります。確かに、人に魚を与えても1日で食べてしまい、釣りを教えれば一生食べていけるわけですが、この格言は教育の現場でもしばしば引用され、まさに言い得て妙です。授業も一緒。授業が単に勉強を教える場となってはいけません。こうした入試問題は、「人生の課題解決の知恵を子どもたち自身が獲得できるような授業が求められている」ということを暗示しているようで、厳粛に受け止めなければならないと思っています。
話は変わりますが、1月21日の記事で触れた大学共通テストのプレテストでも、生徒と先生の会話、生徒同士の議論といった「会話形式」の中での問題がほぼ全ての科目にありました。次は、平成30年の数学Ⅱ・数学Bの問題です。
花子: これは前に授業で学習した漸化式の問題だね。まず,・・・・の形に変形するといいんだよね。
太郎: そうだね。そうすると公比が・・・・の等比数列に結びつけられるね。
花子: 求め方の方針が立たないよ。
太郎: そういうときは,・・・・を代入して具体的な数列の様子をみてみよう。
花子: ・・・・となったけど…。
太郎: 階差数列を考えてみたらどうかな。
「こういう数学的会話が教室で本当に展開されるのかな?」「正直、こんなに物分かりのよい生徒はいねぇよ!」といった受験生の斜に構えたような感想も多数あったようですが、共通テストも高校入試も、形としては全く同じ傾向です。結局、大学入試が変化しているので、高校入試も変化していると考えるのがもっとも自然といえるでしょう。
そのような思いで大学入試センターのHPに公開されているプレテストの問題を改めて眺めていて面白いことに気付きました。
作問の在り方をつくづく考えさせられます。「超駄」かもしれませんし、少々長くもなります。お暇な方はおつきあいください。これは、平成30年のプレテストの国語の古文の問題の最後の設問です。源氏物語からの出題でした。以下に抜粋します。なお、○○や△△、・・・などは、それぞれコッテリした文言が入っていますが、この問題を考える際には全く関係ないので省略しています。
二重傍線部の解釈として、会話の後に六人の生徒から出された発言のうち、適当なものを二つ選べ。ただし、解答の順序は問わない。
生徒A: 私は○○だと思います。
生徒B: そうかなあ。私は△△だと思います。
生徒C: 私はAさんの意見がいいと思う。つまり・・・ということになるね。
生徒D: 私もAさんの意見でいいと思うけど、✕✕に関してはCさんとは意見が違って・・・・。
生徒E: いや、私はBさんの意見ほうが正しいと思うよ。・・・だから。
生徒F: 私もBさんの意見のほうがいいと思う。でも、・・・だよ。
「これって本当に対話だろうか?」、そのような思いはとりあえず置いておき、単純な組み合わせの問題と捉えると、6C2で15通り(AとB、AとC、AとD、AとE、AとF、BとC、BとD、BとE、BとF、CとD、CとE、CとF、DとE、DとF、EとF)の組み合わせが考えられます。
ここで、話の流れを吟味してみます。まず生徒Aと生徒Bが大きく2つの異なる見解を出して、それに対して生徒A側に賛同する立場から、生徒Cと生徒Dが異なる見解を補足しています。同様に生徒B側に賛同する立場から生徒Eと生徒Fが異なる見解を補足しています。そのことは、・・・等で本質的な所を抜いたこの会話からでも見抜けます。
Aの意見に賛同しているのはCとDであり、Bの意見に賛同しているのがEとFであることを考えあわせると、まずAとBで大きな二者選択になってしまうので、AとBの組み合わせを即削除、そして、AとE、AとF、BとC、BとDの4通りも論理的にあり得なくなり、すぐに除外が可能です。
同様に考えると、CとD、EとFも矛盾しているし、CとE、CとF、そしてDとE、DとFもヘンな組み合わせとして除外できます。
結局、AとC、AとD、BとE、BとFの4通りのうちどれかという問題です。実際、この問題の正解は、BとFです。
よ~く考えるまでもなく、二重傍線部の解釈を誤り、最初の選択であるAかBの選択を誤るとAとCやAとDを選択しかねず、その場合全滅してしまう可能性があります。この問題の配点は1問7点であり、2問で14点という今回の国語のプレテストの中では最大の配点になっていました。14点ゲットできるか0点か、この差は実に大きいと思います。こんなときは、「矛盾していることは重々承知でAとBを選ぶと7点は確保できるんじゃ?」とかやけくそ気味に考えた受験生がいたかもしれません。
そういうことで、生徒たちが対話や議論する問題で思考力・判断力等を問う問題を作問するのは、難しい一面があると考えさせられたところでした。
【校長】
What is your belief?
1月最後の週が始まりました。3年生は今日が最後の授業日、そして明日から学年末考査です。3年間の集大成の試験になります。全力で取り組んでください。
ところで、先週の週末、特に26日(土)は、時折雪が舞う大変寒い一日でした。生徒の皆さんはどのようにお過ごしでしたか?
私は当日、九州ルーテル学院大学で開催された「英語スキットコンテスト」の応援に行きました。今回で3回目になるこのコンテスト、県内の公立、私立高校から合計46チームが出場し、本校からもA、B2チームが参加しました。
スキット(skit)とは、「寸劇」を意味します。参加者2〜3人で構成する1チームが英語の台詞による寸劇(3分以内)を行い、内容・演技・英語による3つの基準で得点を競う方式で実施されました。
今回のテーマは、"belief"(信念)です。「あなたの『信念』は何ですか?」と、いきなりマイクを突きつけられたら多くの人がたじろぐと思います。心の軸とも言える「信念」、これを3分以内でどうコミカルにまとめるか、演技力や英語力の前に劇の構想力が問われます。
Aチーム(星原夢杜【1MB】君・平川皇樹【1MB】君・玉村慶太【2MA】君)は、"The world of AIs and human beings"のタイトルで、AI(人工知能)と人間がものづくりの大会で勝負します。その結果はいかに?
Bチーム(中島洸志【1AT】君・畑早和【1AT】君・段村冷美【2AT】さん)が演じたのは、宮大工を目指し日々技術の修練に励む高校生が、前が見えない壁にぶつかっているという設定です。そこに通りかかった同級生が・・・・。タイトルは、"Where there is a will, there is a way"(「意志あるところに道あり」の意味)で、ある意味"belief"の言い換えと言っていいかもしれません。
それぞれ、生徒たちが頭をひねって考えたシナリオと聞きました。一月ほど前、シナリオを読ませてもらったときから、「実に工業高校生らしい着想で面白い!」と、ずっと期待していました。
本番はミスなく、練習してきた最善の演技を多くの観衆と審査員の前で披露することができました。周りの先生方からの感想も好評なようで、ワクワクして結果を聞きましたが、残念ながら2チームともに決勝コンテスト進出は叶いませんでした。会場を後にしようとしたとき、「非常にメッセージ性のある、いいスキットだと思った。そのことを是非お伝えしたかった」と、わざわざ言いに駆けつけてくださる他校の先生もいて、嬉しく受け止めたところです。
次回大会での決勝コンテスト出場と上位入賞を目指して、また新たな取組みが始まることでしょう。他の球磨工生にとっても良い刺激となること間違いありません。私、残念なことに英語がよく聞き取れず半分も理解できませんでしたが、表情豊かにプレゼンテーションをする高校生たちに圧倒される半日になりました。
英語科の先生方には毎日遅くまで御指導いただきました。大変お世話になりました。また、保護者の皆様には応援ありがとうございました。
【校長】
大学入試が変わる
本日から県立学校の前期(特色)選抜の出願が始まりました。前期選抜は、本校の各科に関する学習に興味・関心があり、意欲的積極的な志望動機を持つ受験生の中から、その多様な能力や適性、意欲や関心、努力の成果などの優れた面を積極的に評価して選抜するものです。願書を託された中学校の先生方が次々と手続きに訪れ、受験シーズンが本格化した感がします。
本校を目指す受験生の皆さん、体調に気をつけて頑張ってください。
ところで、昨日、一昨日と「大学入試センター試験」が実施されました。全国で50万人余りが受験したとあって、テレビ等でも大変大きく報じられました。その中で必ず言い添えられたことが、「センター試験は来年2020年1月実施(2021年度入学者向け入試)を最後に廃止され、2021年からは、『大学入学共通テスト』(新テスト)が実施される」というものでした。
今の高校1年生以下は、この新テストを受験することになります。
本校生の大半が就職を選択しており、進学では国公立系でも工業高校枠の推薦入学制度を活用している者がほとんどで、今年度はセンター試験を受験した生徒はいませんでした。しかし、昨年度、一昨年度それぞれ1人ずつではありましたが、受験生がいたことは事実です。「入試制度が変わる」という報に接し、高校1年生やその保護者、中には中学3年生やその保護者の皆様の中にも、漠然とした不安をお持ちになられた方も多いのではないかと案じております。
今日は、大学入試の試験内容等がどう変わるのか、本校としてどう対応しようとしているのかを簡単にご説明をします。
「グローバル化や第4次産業革命に対応しうる人材を育成するため、新しい学力評価制度・大学入試制度の設立が必要である」ということが、この入試改革の背景にあります。文部科学省HP内の「大学入学者選抜改革について」では、そのような人材育成のためには、「学力の3要素」である①知識・技能、②思考力・判断力・表現力、③主体性を持って多様な人々と協働して学ぶ態度、の3つを育成・評価することが重要であると記されています。
では、具体的に何がどう変わるのか。センター試験にはなくて、新テスト(共通テスト)に新たに導入・変更されるものが3つあります。1つ目が「記述式問題」、2つ目が民間の検定試験を活用した英語の「4技能評価」、3つ目は提出書類に「志願者本人の記載する資料」等が加わるなど「調査書等の見直し」です。
まず1つ目です。現行の「大学入試センター試験」は、正解を選択肢の中から選ぶだけの出題形式ですが、新テストでは記述式の問題も加わることになります。このことで、「自らの力で考えをまとめさせたり、相手が理解できるよう根拠に基づいて論述させたりすることで、思考力・判断力・表現力が評価できる」としています。また、高校や中学校では「主体的・対話的で深い学びに向けた授業改善」が促され、大学では高校で身につけた「思考力・判断力・表現力」を前提とした質の高い教育の展開が期待できるとされています。
2つ目の英語の「4技能評価」。これは現行「大学入試センター試験」で実施されている「読む」「聞く」テストに、「書く」「話す」技能の評価を加えようというものです。急速に進むグローバル化へ対応するために、コミュニケーション重視の英語教育が一層求められていることが背景にあるわけですが、この「書く」「話す」テストのノウハウは、民間の検定試験実施会社の開発が相当進んでいるので、それを活用しようというものです。ケンブリッジ英語検定、TOEFL iBT、TOEIC(L&R・S&W)、実用英語技能検定(英検)などが共通テストの「英語」の試験として、成績提供システムに参加することが決定しています。受験生は、高校3年生以降の4月~12月の間に受験した2回までの検定試験の結果を共通テストの成績として、大学に提供することになります。
3つ目の「調査書等の見直し」。これは、「主体性を持って多様な人々と協働して学ぶ態度」を評価するため、高校生一人一人が積み上げてきた大学入学前の教育活動を評価することを目的としています。現行の調査書は、A3見開き1枚の様式となっていますが、この制限を撤廃して、より弾力的に記載できるようにするため、2021年度入試では調査書に記載される内容量がさらに増えるほか、「志願者本人の記載する資料※」の提出が求められる予定です。これは大きく、①活動報告書(「総合的な学習の時間」等において取り組んだ課題研究等、生徒会活動、部活動、ボランティア活動、資格・検定等、各種大会・コンクール等、学校の内外で意欲的に取り組んだ活動など)、②大学入学希望理由書や学習計画書(各大学の学部等の教育内容を踏まえ、入学希望理由や入学後に学びたい内容・計画、大学卒業後を見据えた目標等)からなり、志願者本人が記載するものです。
この大学入学者選抜改革、記述式の導入により、これまで可能だった自己採点ができなくなります。また、50万枚を上回る答案に対してどう採点委員を確保して、採点基準のレベルを合わせるのかも気になります。マスコミも盛んに報じているように、高校、大学双方から批判を含め様々な視点から意見が噴出しているわけですが、レールは敷かれてしまいました。大学全入時代と言われる今でも、大学入試は当事者にとって一生の一大事であり、高校側はその対応が早急に求められています。
御存じのとおり、大学入試センターは「大学入学プレテスト」と称して試行テストを平成29年と30年の2回実施し、思考力・判断力・表現力を問う記述式の問題とは一体どういう問題なのか、そのイメージを明らかにしました。本校の先生方にも問題の分析と、日頃の授業への反映をお願いしたところです。
また、教務部を中心に「主体的・対話的で深い学びに向けた授業改善」の視点を持った研究授業を企画し、思考力・判断力・表現力の育成を目指すとともに、記述式の問題への対応も意識した授業を展開しています。例えば、英語科の授業では、工業科目とも協働し、生徒の発信力を高め、英語を「書く」「話す」活動にアクティブに取り組めるよう、研究・実践を進めています。
さらに、「志願者本人の記載する資料」のうち①活動報告書については、今年度から各行事や学期の終わりごとに生徒たちに記述式の振り返りを求め、ポートフォリオ(学習の過程や成果などの記録を、計画的にファイル等にためておくこと)として記録を残すことを始めたところです。
これらの取組はまだ緒に就いたばかりですが、県内の他の工業系高校とも情報交換を密にしながら、新しい入試制度に向かって用意周到に対応するつもりです。
※「志願者本人の記載する資料」のうち、①活動報告書は、文字通り生徒が活動したことについて記述します。つまり、活動した生徒だけが書けることになります。ボランティアを積極的にしたり、資格試験に意欲的にチャレンジしたりすればするほど充実した報告書が書けるわけです。この報告書が提出できると、入試の際に加点の対象になることが十分に考えられます。また、本校では全員が課題研究に取り組みますが、研究の中心的なリーダーとなって取り組んだ生徒と、先生やリーダーに指示されたことだけに取り組んだ生徒とでは報告書の内容に違いが出てくることは明らかです。高校生活をより主体的に送り、充実させることで報告書の内容も豊かで充実してくることでしょう。
②大学入学希望理由書や学習計画書は、大学に入って自分が何をどのように学びたいのかを詳細に記述します。大学側はこれまで学力で受験生をふるい落としていました。しかし、現在「大学全入時代」と言われるように、大学の定員数と大学進学希望者数に差がありません。受験生はより好みさえしなければどこかの大学には入学できます。そのような中、学ぶ目的意識が乏しい学生が入学後に伸び悩むことを目の当たりにし、苦慮している大学側としては、「入学後も主体的に学んでいく学生を取りたい」という意識に傾くのは当然であり、「大学で学べること」と「生徒が学びたいこと」のマッチングがより重視されるようになっているわけです。
本校では、大学進学だけではなく、就職に関しても、将来どのような仕事をしたいのか、その仕事をするために自分に足りないものは何かを考えさせることにも力を入れています。
【校長】
月やあらぬ

インフルエンザ等での不参加者もなく、197人全員が6時5分、無事出発しました。
保護者の皆さまには早朝からの送迎、大変お世話になりました。事故・怪我なく旅程が進み、楽しい思い出を沢山作ってきてほしいと願っています。

「梅に鶯」連想で、その梅の木にウグイスが来て「ホ~ホケキョ♪」と鳴いている写真を撮ろうと昨日10分ほど待ってみましたが、とうとう来ませんでした。写真部の生徒たちが校内で「一瞬」を狙っている姿を時々目にし、その粘り強さに頭が下がります。私は早々引きあげました。
鳥のことを解説したあるサイトに、「梅の木に止まっている鳥はメジロの可能性が非常に高い。ウグイスとメジロは姿が似ているのと、メジロはウグイスの鳴き声と同じタイミングで梅の木に止まるため、ウグイスと勘違いする人が大変多い・・・」とかありました。私、メジロとウグイスの見分けはつきません。もし写真が撮れていたら、あわや梅の木に止まるメジロの写真を誤ってHPに載せるところだったかもしれません。冷や汗ものです。
梅の花について誰かと話すと、意外なことに桜より梅の花のほうが好きだという人が多いように思います。桜の花の儚さの美しさに対して、梅の花は何かしら力強さを感じます。その香りにも魅せられている私は、今年楽しみにしていることがあります。人吉市大畑(おこば)町の「人吉梅林」を訪ねることです。市のHPによると「白加賀(しらかが)や青軸(あおじく)を中心に、鶯宿(おうしゅく)など白桃系統も合わせた約4,600本の梅の花が咲き誇ります。周辺一帯は梅の香りに包まれ、白やピンク色の花が広大な斜面を彩る優美な世界に・・・」とありました。ずっと前から一度行ってみたい・・・と思っていました。せっかく縁あって人吉で勤務しているのに、昨年は都合で行けなかったので今年こそ。催事も行われる2月24日(日)が待ち遠しいです。できれば、昨年9月に大畑駅に開業したフレンチレストランにも足を運んでみたいです。
最後に・・・、梅ときたら私にとっては「鶯」じゃなくて、「月やあらぬ」が条件反射です。
恋人を失った男が、去年の春にその恋人とともに過ごした、もう住む人のいない家を訪れて詠んだ在原業平のこの和歌、切なすぎます。

あなたと共に見上げたあの月も、あなたと一緒に芳しい梅の香りを楽しんだ春も、そしてあなたまでもお隠れになり、私の周りのものは何もかも変わってしまった気がする。私だけは元とのままで変わらないのに・・・と、世の無常と手が届かない所に行ってしまった恋人に思いを馳せ嘆いている歌だと高校の時に教わりました。
伊勢物語の4段の悲恋をもとにしたラブストーリー、我が家の本立てにもそのコミック本があります。
間もなく別れの季節、3月がやってきます。
【校長】
2019年と国道219号線のワクワクする関係
明けましておめでとうございます。皆様には希望に満ちたいい新年をお迎えになられたことと思います。今年も本校のHPをどうぞ宜しくお願いします。
さて、生徒の皆さん方はお正月、いかがお過ごしでしたか?
球磨川では早くも3日に、寒風を衝いてカヌー部が初こぎをしたと報告を受けました。
私はというと、学校に通う子がいた頃は、元日の朝はそれなりの緊張感があったように記憶しています。でも、みんな巣立ってしまった今、大きな感慨もなくこたつの中で本を読んだり、始業式で何を語りかけようかと考えたり・・・そんな数日間でした。
とはいうものの、これから1年間お世話になる新年号の2019という数字には何かしらワクワク*するものがあります。
既に昨年11月27日の記事でも話題にした通り、2019は3×673と素因数分解され、2つの素数の積として表される「半素数」です。そして、今日を含め残り114日になった平成31年、この31は素数です。
早速、1から9までの数字をこの順に並べて、加減乗除等を施して2019と31を作る小町算をしてみます。
1+2345-6×7×8+9=2019
1×2+345×6-7×8+√9=2019
-1+2+(3!)!!!-45+6×7×8×9=2019
(1×2-3×4+5+678)×√9=2019
{(1+2)!-3}×(4!!-5!!!+678-√9)=2019
12×3+4×5-6×7+8+9=31
12÷3+√4-5+6+7+8+9=31
(1+2+3)×4+56÷7+8-9=31
1×2÷3×4×5×6-7!!!-8!!!!!+√9=31
sin-1(1/2)-tan-1(√3)-4+(5-6)×7+8×9=31
どちらもとりあえず5通りずつできあがりました。まだまだできそうな気がします。
昨年12月19日の記事でも触れたとおり、6[+]4[×]7[-]5=29 程度ではありますが、小町算は就職試験のSPIの常連で筆記試験でも多くの企業が出題しています。日頃からこういう機会を捉えて、紙と鉛筆を持って実際に試行錯誤しておくと、数に関する感覚が磨かれ備えは万全になるはずです。誰も考えつかないという渾身の一式ができあがったら是非教えてください。
暇つぶし?のついでに、今年の素数日も調べてみました。
素数日とは、2019年2月21日を20190221のように8桁で表すと素数になる日です。ネット上の「素数一覧」のサイトから拾い出した今年の素数日は次の19日です。
20190221、20190227、20190301、20190319、20190323
20190421、20190523、20190529、20190601、20190613
20190719、20190811、20190823、20190913、20191009
20191027、20191109、20191117、20191231
和暦(平成31年)ではどうなんだ?と、考えるのは自然なことです。このまま何も起きなければ、1989年1月8日に始まった平成は、11070日続いて、今年の4月30日に終わることになります。31****のような6桁表示の素数日は次のとおりわずか7日でした。
310111、310117、310127、310129、310223、310313
310423
工業高校で学び数字とは縁が切れないはずの皆さん方に、数字を見る目や数的処理のセンスが高まるようにとの願いを込めて、今年もこのサイトを充実していくつもりです。どうぞ宜しくお願いします。
最後に・・・、本原稿は下の注釈まで合わせて全部で2019文字です。
【校長】

ちなみに、八代市から人吉市までの約40kmの間に「国道219」の看板が全部で何箇所立っているか数えたことがあります。全部で27箇所でした。平均して1.4kmに1回、219という数字が嫌が上でも目に飛び込んできます。

先ほども触れたように、2019のほうは、2019=3✕673 でした。
どちらも3という素因数が共通しています。これがワクワクする原因でした。
ワクワクしたついでにちょっとしたクイズを作ってみました。下の①~⑤に当てはまる数字は何でしょう?数学検定3級程度の規則性を見つける問題です。
3✕ 73= 219
3✕173=【 ① 】
3✕273=【 ② 】
3✕373=【 ③ 】
3✕473=【 ④ 】
3✕573=【 ⑤ 】
3✕673= 2019
答 ①:519、②:819、②:1119、③:1419、⑤:1719
※300ずつ増えている理由は?
鹿と3に関連したクイズをもう一つ。漢和辞典で一番画数の多い漢字は何でしょう?
憂鬱(ゆううつ)の鬱ではありません。29画です。答は鹿を上に1つ下に2つ計3つ書いた「麤」で33画です。この漢字は「粗」と同じで、音読みは「ソ」、訓読みは「あらい」と読むようです。ちなみに牛3つの犇は「ひしめく」と読みますが、驫や猋、羴という漢字もあります。何と読むか知ってますか?猫が3つの漢字は見つかりませんでした。
平成30年度の就職試験を振り返る
就職試験ではどのような問題が出題され、面接で何が問われたのでしょうか。概要を知っておくことは学校を預かる責任者として大事なことであると思い、3年生の皆さん方が提出した受検報告書に毎年目を通しています。
集団討論で「日本食と言えば寿司か蕎麦か」というお題で議論させた企業がありました。一体どんなことが話し合われたのだろうと興味津々です。
また、計3社で「中学校で必須教科を1つだけ加えるなら何か」と面接で問い、「学校の教科で1つ増やすとすれば何か。理由も添えて述べなさい」と作文で出題していました。昨年度は、「祝日に1日付け加えるとしたら何?」とあり、「エッ?!」と思ったところでしたが、今年は「教科」です。一体どのような答を期待しているのでしょうか。もし学生時代に学び足りなかったことを聞いているのだとしたら、私なら「年金制度」と答えるかもしれません。
ということで、いくつかの問題を紹介します。(【 】内に地区と業種を示しました。3社以上で出題があった問題は【多数】と表記しています)
1、2年生の皆さん方は、このような問題に来年、再来年に直面します。今の実力でどのくらい対応できますか?
作文
・「入社3年後の目標」(「20年後の自分について」「社会人になってチャレンジしたいこと」「目標を達成するために継続して努力したこと」「社会人になるに当たっての心構え」「大工になってやってみたいこと」等も)【多数】
・「高校生活で一番困難だったこと」(「それをどう乗り越えたか」「その結果何を得たか」「それを今後どう活かすか」「今まで一番打ち込んだこと」「私が一番自信をもっていること」等も)【多数】
・「働くということはどういうことか」(「私にとって働きやすい職場とは」「仕事を通してどういう力をつけたいか」「働きながら成長するために心がけたいこと」「仕事をする上で大切なこと」等も)【多数】
・「製造業で一番必要なコンプラインアンス意識とは」【中京・製造】
・「学校の教科で1つ増やすとすれば何か。理由も添えて書きなさい」【中京・製造、中京・鉄鋼】
・「あなたを漢字1文字で表現するとしたら何か。理由も書きなさい」【中京・鉄鋼】
・「次の2つの中からあなたが修理できるものを選び、今まで学んだことを活かして修理の手順や必要な道具を詳しく書きなさい」【関東・保全】
①エアコンの効きが悪い ②パソコンでインターネットに繋がらない
・「お年寄りと関わる中で感銘を受けたこと」【熊本・介護】
集団討論
・「皆さん達4人はチームです。4人で会社を起業するとしてあなた達は何を売りますか」【中京・製造】
・「ドラえもんの四次元ポケットがあったとして、のび太君と世界を幸せにする道具をそれぞれ一つだけ選び、その理由並びにその道具の欠点を話し合ってまとめなさい」【中京・鉄鋼】
・「中学校で必須教科を一つだけ加えるとしたら何か」【中京・製造】
・「中高生のインターネットの依存の対策は」【九州・製造】
・「成功体験と失敗体験のどちらが人を成長させるか」【九州・電力】
・「KYT(危険予知訓練)活動。絵を見て危険なところを探し、安全策を5人で討論しなさい」【近畿・製造、中京・製造】
・「東京オリンピックを盛り上げるためには」【中京・製造】
・「社会のルールを守らない人はなぜ守らないのか、その解決策は」【九州・製造】
・「日本食と言えば寿司か蕎麦か」【関東・鉄道】
・「飛行機が故障して砂漠地帯に不時着した。そんな中あなた達5人は12個のアイテムを手にして逃げることになりました。12個の必要なアイテムを挙げて順位を決めなさい」【中京・製造】
・「学生と社会人の違い」【中京・製造】
・「ある企業には野球部があり、ファンクラブもある。同じように部を作るとしたら何部を作るか。チーム名、スローガン、集客方法、資金をどうするか」【関東・鉄鋼】
筆記試験(時事問題系の一般常識)
・「熊本県知事の名前をフルネームで漢字で書け」(「今の内閣総理大臣の名前」、「校長の名前」等も)【多数】
・「熊本城を建てた人は」【熊本・設備】
・「オリンピックの種目で新種目4つのうち1つ答えよ」【関東・電力】
・「自民党の総裁選挙に出馬するのは安部普三首相とあと一人は誰か」【関東・保全】
・「2018年、テニス全米オープンで優勝した選手は」【九州・建設】
・「東京オリンピック、パラリンピックのキャラクターは」【関東・製紙】
面接
・「高校時代に頑張ったこと」【多数】
・「年上の方や上司と仕事をしていくわけだが、どうすると上手く付き合っていけるか」【多数】
・「働くとはあなたにとってどういうことか」(「仕事とは何か」等も)【多数】
・「ジュニア・マイスターとは何か」【多数】
・「あなたが知っている重機の名前は」(「弊社の製品の名前は」等も)【多数】
・「弊社を漢字1文字で表すとしたら何か」(「漢字2文字なら何か」、「あなた自身を漢字1文字で表すと何か」等も)【多数】
・「あなたにとってどのようなことがストレスか。ストレス発散法は何か」【多数】
・「自分を動物に例えるなら」(「自分を車の部品に例えると何か。またその理由は何か」等も)【多数】
・「不得意な科目をどのように努力し克服したか」【中京・製造】
・「昨夜は寮に泊まってもらったが、同室4人とコミュニケーションを取ったか」【近畿・電力】
・「人の意見を聞いて動くタイプか、それとも自分で決めて行動するタイプか」【熊本・製造】
・「初任給をどう使うか」【中京・製造】
・「SNSに関してどのようなことに気をつけているか」【関東・鉄鋼】
・「あなたにとって苦手な人はどんな人か。その対処法は何か」【関東・建築】
・「あなたが住んでいる町の特徴は」【中京・建築】
・「ふりこ、ストップウォッチ、棒の3つを使って振り子の周期を確実に測定する方法は」【熊本・製造】
集団工作等
・紙20枚とはさみ、テープを使って8人で共同して高いタワーを作る。ただし、紙と紙との接合にテープを使ってはいけない。タワーの名称、工夫した点を話し合い、代表一人が発表。【中京・製造】
・ミニゴルフで得点を競う。(各班7人。まず、司会1、書記1、タイム1、応援2を選ぶ。選手と各係は重複可。各グループで「動作手順」を作成し、その手順通りに選手1人が3球ずつ打って3人の選手の合計点を班ごとに競う。その後、上手くできた点、できなかった点を面接で聞かれる)【中京・鉄鋼】
・マシュマロタワーにチャレンジ!【関東・電力】
パスタの乾麺20本、テープ90cm、たこひも90cm、マシュマロ1個(頂上につける)これらを使ってより高いタワーを4人で作りあげる。(説明5分、個人ワーク5分、作戦タイム13分、制作20分、反省10分)
まとめ
作文のお題は、毎年定番のものばかりです。面接では、社会の出来事を反映した時事問題を問う企業があるようです。グループワークや集団討論を課す企業が年々増え、採用に当たりコミュニケーション能力重視の姿勢は一貫したものを感じます。また、昨年度と同じ出題が続いている傾向が非常に顕著で、過去問をしっかり解いておく必要性を痛感します。
最後に・・・、生徒諸君が残していた感想には、「工場内は5Sが徹底していて、ゴミ、油など全く落ちていなかった」、「工場内は隅々まで掃除が行き届いており、さすがだと思った」などが沢山あり、普段から5Sを口うるさく指導している成果が出ているな・・・と嬉しく思ったところでもあります。
【校長】
追伸
・6□4□7□5=29 【多数】
□に+,-,÷,×を入れて式を完成させる問題を短時間にできるだけ沢山解くもので、SPIの常連で筆記試験でも多くの企業が出題しています。ちなみにこの答は順に+、×、-
このような算数系の問題(小町算)は、普段から私のサイトを見て数に関する感覚を磨いておくと得意になるかもしれません。
この問題を見て閃きました。今日12月19日は、今年最後の素数日*です。それを記念して日にちの数字をそのまま並べた1219をこの式で作ることができないかということです。即ち
6□4□7□5=1219
暫く考えたところ、何と全部「+」だけでできあがりました。
6!+(4!!)!!+7!!+5!!!=1219
「階乗、しかも多重階乗なんか使ってずるい」と言われそうですが、「+だけでというのが凄い偶然だ」と思わず唸ってしまいました。何かいいことがありそうです。
*素数日とは
平成30年12月19日を301219のように6桁で表すと素数になる日です。このことについては、今年1月1日の記事で一度紹介したところですが、改めて書き出すと以下の通り24日あり、今日は今年の最後の素数日になります。
300109、300119、300221、300301、300317、300319
300323、300331、300413、300427、300511、300623
300719、300721、300809、300821、300823、300929
301013、301027、301123、301127、301211、301219
西南戦争と人吉、そして村山台地
俳優の鈴木亮平さんが主演を務めるNHKの大河ドラマ「西郷どん」が昨夜とうとう終わってしまいました。最後2回は「西南戦争」での激しい戦闘の様子が圧巻でした。
言うまでもなく、西南戦争(西南の役)は、1877年(明治10年)に九州で、明治新政府に対して反感を持っていた鹿児島の士族達が西郷隆盛を盟主にして起こした武力反乱です。明治初期に起こった一連の士族反乱の中でも最大規模のもので、我が国最後で最大の内戦と言われています。
平和的な交渉を望んだのに賊軍となってしまった西郷軍、「最後の侍」として日本のために使命を全うし、こうやって歴史になっていってしまったのかと感無量の思いで見ました。
ところで、生徒の皆さんは、ここ人吉市が西南戦争の激戦地の一つだったということは大丈夫ですか。「西郷どん」では先週(第46話)、解説字幕で「人吉」という地名がほんの一瞬出ただけでしたが・・・。
そして、この戦争が献血等の際にお世話になっている日本赤十字社*発足のきっかけになったということは知っていましたか?(「西郷どん」ではこのことは扱われなかったようですが・・・。)
本校の校歌の1番は、「ふるさとの文化の朝に 風さやか村山台地♪」の出だしで始まります。本校が所在するこの村山台地こそ、西南戦争を語るうえではずせないキーワードになります。
その説明書きや史料によると、薩摩軍は、九州を北上し、熊本城を攻めますが、中々うまくいかなかったようです。1873(明治6)年3月、田原坂の戦いで敗れた薩摩軍は熊本城をあきらめ、追ってくるであろう官軍を迎え撃つために人吉にしばらくの間滞在しました。西郷隆盛は永国寺に本部(宿舎)を置いて戦争の指揮を執ることにし、球磨川南岸に兵を集結しました。
一方、薩摩藩を追って人吉に入った新政府軍は、人吉城下を一望でき見晴らしの良い村山台地に砲台を築きました。6月1日、眼下球磨川に展開する薩摩軍への総攻撃を開始。球磨川を挟んで砲火が飛び交いました。薩摩軍には人吉の士族たちも多数合流していましたので、父子、兄弟、甥と叔父が敵味方に分かれて戦ったとありました。(こういう記述は、中世の保元の乱(1156年)を彷彿させます)
薩摩軍の砲弾は、政府軍の本営まで届かず、球磨川を挟んでの攻防は官軍の圧勝で終わり、薩摩軍は、町に火を放って人吉から退却。町は、戦闘と放火により、灰燼に帰しました。それだけでなく、この人吉根拠地の期間中、薩摩軍はこの地域に苛烈な軍政を布き、政府軍と内通した容疑をかけられた住民が捕縛され、証拠も詮議も不十分なまま私刑同然に処刑する残虐が加えられているそうです。薩摩軍は総崩れとなって敗走、人吉を捨てて田代、大畑方面へ退却し、大畑に陣を敷きます。・・・以下省略します。
昨年は西南戦争後140年目に当たるということで、当時を振り返る催しが各地で行われたり、関連本も沢山出版されました。興味がある人は調べてみると、自分が住む人吉について新たな発見があるかもしれません。
また、いつの世も高台というのは戦局を有利に進めることが多いわけですが、本校はそんな悲しい歴史が残る村山台地に所在していることを知っておくことは大事なことかもしれません。
【校長】
*昨年の夏休み期間中に生徒会の生徒たちが、「青少年赤十字リーダーシップ・トレーニング」という活動に参加してきました。生徒たちがもらってきたガイドブックの中に赤十字の歴史について次のように触れてあります。以下、長くなりますが抜粋しておきます。(参考までに)
日本赤十字社もスイスで最初の赤十字が誕生した時と同じように、戦いがきっかけで誕生することになりました。戦いに大きな力をもっていた鹿児島の士族である反乱軍は熊本まで攻め上がり、熊本城や田原坂を中心に明治政府と反乱軍で激しい戦いが繰り広げられ多くの負傷兵が出ました。負傷した兵士の多くは戦場に倒れたままで、充分な看護も受けられず苦痛に耐えかね、お互い刺殺しあった者もいたと言われています。
九州での悲惨な戦いを東京の地で聞いて悲しく頭を痛めていた元老院(今の国会)議官の佐野常民は、負傷した兵士がなんの救護も受けず放っておかれていることが残念でなりませんでした。
佐野常民はこれまでにヨーロッパを旅行したことがあり、その時にヨーロッパには戦場の負傷兵を敵・味方の区別無く救護する赤十字という団体があることを知っており、日本でもそのような団体を作る必要があると考えていました。この西南戦争の時に、赤十字のような団体があれば、負傷兵の生命を救うことができると考えたのです。
そのことを友人の元老院議官の大給恒(おおきゅうゆずる)に相談したところ、大給恒も大いに賛成してくれ、2人は具体的な計画をまとめました。救護団体を作りそれを博愛社と名付け、明治政府に救護活動をするための願書(ねがいしょ)を提出しました。
しかし、願書に記されていた敵・味方の区別無く救護するという考えは当時の人々になかなか受け入れられず、明治政府は、政府に逆らう反乱軍の兵士まで救護するという趣旨のこの願書を認めませんでした。
佐野常民はあきらめませんでした。認められなかった願書を持って戦場の熊本へ向かい、熊本城で政府軍の総指揮者として反乱軍の鎮圧にあたっていた有栖川宮熾仁親王(ありすがわのみやたるひとしんのう)のもとへ、直接博愛社の設立の許可を願い出たのです。有栖川宮熾仁親王はこの願いを聞き入れ、その場で博愛社の設立を許可しました。
1877年5月1日のことです。日本赤十字社の創立記念日はこの日を記念して5月1日としました。これにより「博愛社」の救護員は直ちに現地に急行し、両軍の負傷者の救護にあたりました。この活動は、当時、敵の負傷者まで助けるという考えが理解できなかった人たちを驚かせました。
西南戦争から9年たった1886年(明治19年)、明治政府はジョネーブ条約へ加入しました。そして、博愛社は翌年の1887年(明治20年)に名前を日本赤十字社と改めることになり、ここに日本赤十字社として国際赤十字の一員に加わることになりました。
さらに1919年には、赤十字の平時活動を推進する国際赤十字・赤新月社連盟の創設に参画しました。
今日では、戦時平時の別なく幅広く赤十字の活動の推進に努めています。
長距離走大会と心拍数
いつも本校のHPにお越しいただきありがとうございます。

途中で3人がリタイアしましたが、その他の生徒たちは全員が規定時間内(2時間)に走り抜くことができました。
力強い走りでみんなを先導した男子1位の鶴田舞杜君【3MA】(43分3秒:302.0m/分)、女子1位の千代村春花さん【1A】(48分6秒:228.7m/分)をはじめ、上位15人の皆さん方を表彰しました。そして、団体の部では2MBが優勝しました。誠におめでとうございます。
沿道周辺の皆様には、今年も大変御迷惑をおかけしましたが、終始温かいご声援をいただきありがとうございました。また、保護者の皆様には豚汁を振る舞っていただき大変ありがとうございました。

1113、この数、どこかで耳にした数だな・・・と思って記憶の糸を手繰ったら・・・何と昨日、買い物をして支払ったお金でした。
1113円
ある意味、凄い偶然です。
1113は1113=3×7×53と素因数分解されるので、素数ではありませんが(約数は、1, 3, 7, 21, 53, 159, 371, 1113の8個)、今日12月13日の数字をそのまま並べた1213、こちらは素数です。
偶然といえば、凄いことが今朝起こりました。3日前(12月10日)の記事で1248421という数がアクセスカウンター以外で実際に現れるとしたらどんな場面なのかと話題にしました。
何と、それに近い数字が今朝現れたのです!
私、毎朝、手首式血圧計で血圧を測っています。最高血圧●●●mmHg、最低血圧▲▲mmHg、脈拍数★★拍/分 をそのまま並べると、●●●▲▲★★という7桁の数になります。今現在、学校のHPの総アクセス数が7桁を刻んでいますので、血圧計が表示した7桁の数とHPの総アクセス数が極々小さな確率ですが同じになる可能性があります。そういう日がいつどんな状況で現れるのか、毎日楽しみに血圧を測って、表示された数字を眺めています。

気になって心拍数が20前後の動物を検索したところ、ありました。象です。象で思い出すことがあります。生徒の皆さんは「哺乳類の心拍数と寿命は反比例し、一生の総心拍数は約20億拍で一定」という学説を聞いたことがありますか?有名ですから、耳にしたことがある人は多いかもしれません。
それによると、象(20拍/分)の寿命は、20億÷(20×60×24×365)を計算しておよそ70年、ちなみに人(70拍/分)は、20億÷(70×60×24×365)で、およそ54歳になります。(現在、人の平均寿命は男女とも80歳を越えていますが、医療と食生活の進歩によるものと考えられているようです)
とにかく、体が大きい(体重が重い)動物ほど1分間の心拍数が少なく長生きで、体が小さい(体重が軽い)動物ほど心拍数が多く寿命が短いという「心拍数と寿命の間の反比例の法則」そして、「哺乳類の心臓は総心拍数が20億回で打ち止め仕様」、どちらも味わい深い説です。
心拍数が少ないほど長生きできるというのなら、中・高校生の時にしっかり運動をして心肺機能を高めておき、平常時には70拍/分よりも低い、例えば60、50拍/分といった心拍数で動く強靱な心臓を作っておけば長生きできるということでしょうか?それとも、運動をやっていると、その分当然心拍数の増加を伴うので、やっただけ寿命が短くなるということでしょうか?
若い時に作った身体で残りの人生を生きていくというのは確かですが、こういうことが運動生理学などに無知の私にはよく分かりません。
ちなみに本日の長距離走大会でこんな計算をしてみました。もし、最大心拍数200拍/分で1時間半ずっと走っていたとすると、その間に心臓は1,8000回(200×90)打っていたことになります。これは生涯の総心拍数20億回に対してどのくらいの割合になるかというと、0.000009即ち9ppm*になります。この数字、一体どう捉えればいいのでしょう?
今日の長距離走大会、どのくらいまで心拍数が上がったか脈を取った人はいますか?身長や体重だけでなく、心拍数や血圧といった内臓機能についても、自分の身体のスペックとして時には気にしてみましょう。
【校長】
ppm*(パーツ・パー・ミリオン)について
ppmは、「parts per million」の頭文字をとったもので、100万分の1の意味。主に二酸化窒素などの大気汚染物質をはじめとする公害分野や、食品添加物などの濃度、岩石中の微量元素の組成、半導体中の不純物量を示す目的などでよく用いられるが、不良品発生率などの確率を表すこともある。
拵える、誂える、設える

見事な西高東低の気圧配置となり寒い週末でしたが、生徒の皆さんはどのようにお過ごしでしたか?
私は京都の同志社大学に行っていました。京都検定を受験しにです。
2,3年生の皆さんは、昨年2学期の終業式で次のような話をしたことを覚えているかもしれません。
「私、せっかく人吉の地に赴任したから、地元をよく知るためにも『人吉球磨検定』を受けようと決心した。・・・テキストを買って勉強してきたが、願書請求の段階になって実施してないことを知った。・・・受験生が集まらず3年前から休止になっているらしい。・・・ここ人吉は京都と雰囲気が似ていることから『小京都』と呼ばれているが、雪辱を果たすためにも本物の京都検定を受けたい。・・・」と。
一時期ブームになっていたご当地検定、その嵐も過ぎ去り東京の「大江戸検定」、奈良の「奈良まほろばソムリエ検定」、京都の「京都観光文化検定」(これが正式名称)の3つがいまだに沢山の受験生を集めており、その中でも絶大な人気があるのが通称「京都検定」のようです。
私、検定試験を受けるのはおよそ10年前の技能検定以来久々です。この京都検定、今の学校教育で育むことが重要視されている思考力・判断力・表現力等とは(論文が課せられる1級は別として少なくとも2級・3級では)無縁の世界です。ひたすら暗記力だけの勝負で、そういう意味では潔い試験と言ってもいいかもしれません。京都に行ったことは高校の修学旅行を含めわずか3回しかありません。地図を広げ碁盤目状の道路配置を頭に叩き込んだうえで、数多ある寺社を始め色々なことを全て一から覚えていきました。
とは言っても、この歳になると記憶は忘却との闘いです。今日10覚えても次の日には9忘れているといった状態が続き、途中何度か断念しようと弱気になりました。くじけそうになるモチベーションを奮い立たせてくれたのが、主催者が公表しているデータです。それによると、1級~3級のどの級も受験生が一番多い層が50歳~60歳(H28年度)ということで、記憶力の減退に苦しんでいる同志がきっと沢山いるはず?・・・、そのことだけが心の支えでした。
そういうことで、試験勉強では公式テキストに加えて市立図書館や県立図書館にある京都本を読み漁(あさ)りました。特にものづくり関係の本を中心に。そして気付いたことがあります。今日のタイトルにある「拵える、誂える、設える」という動詞です。順に「こしらえる、あつらえる、しつらえる」と読むようです。
京都のものづくり(伝統工芸)については、公式テキストブックの中に次の一節があります。
京都の伝統工芸の「匠の技」は朝廷、巨大社寺、貴族らがスポンサーとなり一流の審美眼で京の伝統工芸にさらなる技芸の精進を促し、これに応える十分な職人芸が発達した。・・・(途中略)・・・宗教都市であり、文化都市でもある京都は、現代でも工芸美術品の需要があり、それが重層的に影響しあいながら類いまれな「手の匠」を生み出しており、国の伝産法(伝統的工芸品産業の振興に関する法律)に基づいて、経済産業大臣が指定する伝統的工芸品に京都府内の17品目が指定を受けている。・・・
これら3つの大和言葉風の響きをもつ動詞、京のものづくりを語る本の中になぜか高い頻度で出てきます。私自身はこれまで稀に耳にしたことはありますが、いずれも自分が普段使う語彙ではありません。それだけにすごく目についたのかもしれません。意味も曖昧でしたから、念のために辞書で調べてみました。
●「拵(こしら)える」とは、ある材料を用いて、形の整ったものやある機能をもったものを作り上げること。
●「誂(あつら)える」とは、自分の思いどおりに作らせる。注文して作らせること。
●「設(しつら)える」とは、ある目的のための設備をある場所に設けること。
語義を読んでも、日常使わない言葉だけに分かったような、分からないような変な気分です。「誂える」は、お金を払って自分ではない他の人(専門家)に頼むニュアンスが強いから、ものづくり系の動詞にも拘わらず「手偏」ではなく「言偏」なのかなぁ・・・?とか思いつつ、このような小難しい動詞が似合う京の一流の職人たちによるものづくりの奥深さに思いを巡らしたところです。
こうした言葉で語られる伝統工芸に限らず、寺社や史跡・名勝から建築、庭園、美術、芸能に至るまで広く(浅く)触れたことで、日本の政治文化の中心であった京都の奥深い魅力を新たに発見しました。その意味で京都検定、私にとってはとても有益でした。また、知識が増えていく楽しみが記憶力低下の厳しい現実を突きつけられる辛さを凌駕してワクワクしたことも実感です。

この数、右から読んでも左から読んでも同じになる回文数です。それに加え、上4桁の1248は初項1、公比2の等比数列をなし、下4桁の8421は初項8、公比(1/2)の等比数列になっているという点でも面白い数です。ちなみに素因数分解すると、素数2つの積になる「半素数」でした。
1248421=29×43049
ですから、その約数は1,29, 43049, 1248421の4個になります。
ちなみに1248421という数がアクセスカウンター以外で実際に現れるとしたらどんな場面でしょう?私、超々気になって検索をかけてみました。
ありました。今、お茶の間の話題をさらっている某自動車メーカーがpdfで公表している売り上げ報告書の中に、次の表記を見つけました。こういう偶然ってあるんですね!
・・・販売台数は、前年比9.4%増の1,248,421台となりました。・・・
最後に、今日取り上げた1248421について、数字の並びをそのままにして、加減乗除等の記号を入れて、この数字が現れた日にちであり、開戦記念日でもある12月8日をそのまま並べた128を拵えてみます。
-1+24+84+21=128
1+2+4×8×4-2-1=128
(124+8-4)×(2-1)=128
1×2×4×8×4÷2×1=128
124+(8÷4+2)×1=128
1+248÷√4+2+1=128
{12√4-(8+4×2)}×1=128
1×2×√4×8!!!!×(4-2-1)=128
12×4!!+8!!!!+√4-2×1=128
{12÷4×8!!!!+(4!!)!!!!}×(2-1)=128
{12!!!!!!+48+4×2}÷1=128
12!!!!!!+sin-1(4/8)+(4!+2)×1=128
cos-1(1/2)+(4!!)!!!-8÷√4×(2+1)=128
tan-1{√(1+2)}+4+8!!!-4!!×2×1=128
ということで、広島~新神戸間の1時間ちょっと間に14通り立式しましたが、まだまだできそうな気がします。皆さんだったらどのような式を拵えますか?誰も考えつかないという渾身の一式ができあがったら是非教えてください。
ちなみに私もサイン・コサイン・タンジェントの全てが入った奇抜な式を立式しようとだいぶ試みましたが・・・
sin-1(1/2)+cos-1(4/8)-4-2+tan-1(1)=129 ×

受験に向かっているのに、小町算なんかで遊んでないで「追い込みの勉強したら・・・?」とか言われそうです。
でも、困ったことにポテチと一緒で「やめられない・止まらない」なんですよね、これが(..;)
【校長】
12月3日→123で思い出すこと
いつも本校のHPにお越しいただきありがとうございます。月が変わってとうとう師走に突入しました。1日(土)は小春日和でしたが、昨日2日(日)は昼から雨が降り出し少々肌寒い天気になりました。期末考査も終わりましたが、生徒の皆さんはいかがお過ごしでしたか?
私は昨日、多良木町で行われていたサイテク祭り( Science & Technology の略らしい)で、本校溶接部と電気工作部がブースを出していたこともあり、様子を見に行きました。天気がぐずついていたせいか、昨年度よりも若干客足が鈍ったということですが(主催者発表)、本校のロボットやUFOキャッチャーの前には写真のように終日賑わっていました。
事業所の皆様には大変お世話になりますが、御指導を宜しくお願いします。
ところで、数日間出張が続いていたので、たまっていた仕事をしようと、今日はいつもより2時間余り早く学校に来ました。到着後すぐHPを開いた時(午前5時45分)の総アクセス数は1242013。
これはどのような数かな?素数ぽいけど・・・と、いつものように素因数分解をしてみました。電卓を暫く叩きましたが、なかなかできません。根負けしてネット上の素数判定機にかけたわけですが、驚くべき事実に気付きました。
まず、1242013 は、先日から話題にしている「半素数」(2つの素数の積として表される数)でした。
1242013=41×30293
従って、その約数は 1, 41, 30293, 1242013の4個です。
何に驚いたのかというと、今日の日にち12月3日の数字をそのまま並べた123*も 123=3×41 と素因数分解される「半素数」であり、しかも41が共通していたということです。
それはさておき、この41という数、なぜか神秘的です。皆さんは、名古屋市と富山市を結び、日本列島をほぼ真っ二つに縦断する国道41号線のことを耳にしたことがありますか?
全長約250キロのこの道沿いから、ノーベル賞受賞者が相次いでいるということで、この国道41号線は別名「ノーベル街道」と呼ばれているそうです。日本でノーベル賞を受賞した方の生家の何と3分の2が41号線脇にあったそうです。右はネット上で見つけたそのことを報じる新聞記事です。偶然にしてはとても神秘的ですよね。
かつては出世魚のブリをはじめとする生活物資が運ばれていたらしいですが、この業績にあやかって「現代のお遍路」をする人たちもいるそうです。
最後に、今日取り上げた1242013について、数字の並びをそのままにして、加減乗除等の記号を入れて、今日話題にした41と123の2つの数を作ることに挑戦してみます。
1+2+42+0-1-3=41
124+2+0!-1-3=123
あまりにも簡単にできて、何だかな~です。もう一組作ってみます。
12×4-2-0!-1-3=41
-1+2+√4+20×1×3!=123
う~ん、ピンときません。もう一組作ってみます。
-1-2×4+2+{(0!+1)×3}!!=41
(1+2)4+{(2+0!)!+1}×3!=123
何通りもできそうですが、皆さんだったらどんな式を作りますか?
*123で思い出すこと
123と聞いて真っ先に思い浮かぶものといえば、33年前、昭和60年(1985年)8月12日に起きた日本航空123便御巣鷹山(おすたかやま)墜落事故です。単独事故としては史上最多の死者を出した航空機事故(乗員15人を含む520人が死亡)でした。
当時、私は教師として駆けだしの頃で、数学の免許を取るために東京の玉川大学の夏期講習会(スクーリング)に2週間通っており、明日帰熊という日でした。
あの日あの時(午後7時頃)、突然テレビの画面が「飛行機が消息不明」と報じるニュースに切り替わった瞬間は衝撃的で、鮮明に覚えています。その後は夜更けまでテレビにくぎ付けとなり、仮眠してはまたテレビを見るといった感じで、生涯忘れえぬ事故になりました。
時を経て、あの大惨事を直接知らない若い人たちが増えてきています。次第に風化が進むのは致し方ないのかもしれません。
そんなことを時々考えていたつい先日、これまた衝撃のニュースが報じられました。何と、イギリスのヒースロー空港で、乗務直前の日本航空のパイロット(副操縦士)から、基準値の9倍を超えるアルコールが検出され酩酊状態だったというものです。2日前の新聞では、現地の裁判所は「乗客乗員を危険にさらし、大惨事を引き起こすおそれがあったとして、被告に禁錮10カ月を言い渡した」と。
副操縦士は42歳とありました。今から33年前といえば9歳になりますから、この事故を直接知らない世代なのかもしれません。しかし、大惨事を引き起こした当該会社の社員ですし、社内教育で「御巣鷹を忘れるな!」と何度も聞き、徹底した安全教育を受けていたはずです。「それにも関わらずなぜ・・・?」という思いが、私たち大人の飲酒運転が無くならないこととダブってしまいます。
パイロットは離着陸の時だけでなく、常に緊張状態を要求される特殊な職業であり、お酒にストレス発散を求める向きがひょっとしたらあるのかもしれません。でも、飛行機の事故はとにかく、とにかく悲惨です。「飛行機をコントロールする前に、自分をコントロールできる人」が操縦する飛行機じゃないと誰しも乗りたくないはずです。
高校生を含めた若い人たちのアルコールの問題に敏感になっている時と偶然に重なったこともあって、今年一番ショックを受けたニュースの一つでした。
【校長】
√1234321=?
いつも本校のHPにお越しいただきありがとうございます。生徒の皆さん、3連休、いずれも天気に恵まれましたがいかがお過ごしでしたか?今日から期末考査が始まりました。全力を尽くしてください。
ところで、本校のHP、最近1日におよそ1100件(1時間当たり45件)のアクセスがあっています。

この数字、ちょっと面白いと思いませんか? 右から読んでも左から読んでも同じ数という意味で。
このような数字を「回文数字」といい、趣味の数学の分野でしばしば研究の対象になっています。このことについては、偶然にも丁度1年前、昨年の11月27日の記事で紹介済みです。(詳しくはこちら → 総アクセス数 842248 → この数字の魅力)

最上桁から数字が昇順に並び、何ともいい数字です。
ということで、今日はこれら2つの数字について考察してみます。
まずは今日のタイトルである √1234321=?
これは数年前の3年生の受験報告書の中にあった、即ち就職試験に出題された問題でもあります。学校では習わないはずの開平法(ルートの近似値を筆算で計算する素朴な方法)の技量を問う問題とは思えません。以下に述べる知識の有無が問われているはずです。
111や11111のように1がいくつも並んだ数字を「レピュニット」(repunit【repeated unitの略】)ということについても、今年の7月17日の記事で紹介済みです。(詳しくはこちら → 総アクセス数1111111と7月17日と239)
その日の記事で、レピュニットに関する頭の体操を3問出題していました。それとも関連する問題になります。
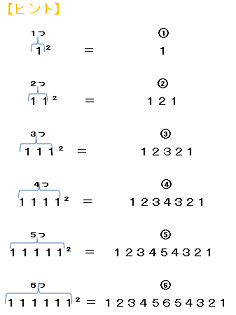
そこから何か閃きません?
・・・・
・・・・ thinking time ・・・・
・・・・
分からない人は左の【ヒント】を見て考えてください。
もう大丈夫ですよね。
4段目の④をみながら、答は1111
では、数としての1234321を考察してみます。まず素因数分解です。
1234321=112×1012
従って、その約数は、1, 11, 101, 121, 1111, 10201, 12221, 112211, 1234321の9個。何と約数まで全て回文数になっているのがある意味不気味です。
次に1234567 果たして、これは素数でしょうか?
色々な素数で割ってみました。なかなか素因数が見つかりません。根負けしてネット上の素数判定機にかけてみたら、素数ではありませんでした。
1234567=127×9721
ということで、その約数は 1, 127, 9721, 1234567の4個になります。
従って、もし「x2+9848x+1234567 を因数分解しなさい」という問題があれば、その答は (x+127)(x+9721)となります。中学程度の因数分解ですが、難しいですよね(..;)
でも、こういう因数分解が某私立高校の数学の入試の1番の集合問題の中に出題されていたのを見たことがあります。勿論、最後の定数項は1234567みたいな7桁の数字ではなく4桁の数字でした。その数字、随分昔のことで正確に覚えていませんが、例えば「x2-670x-2019を因数分解しなさい」ならできますか?
2019は来年の西暦です。閃き力を問う問題かもしれません。
答は(x+3)(x-673)です。定数項はわずか4桁ですけれども、当時、因数分解の専門書の中で「高校受験史上最難の因数分解」とか騒がれました。実際、限られた時間で3と673の組み合わせを見つけるのは至難の技かもしれません。
知っている人もいるかもしれませんが、1234567のように2つの素数の積として表される自然数のことを「半素数*(semiprime:【セミプライム】)」と言います。素数は無数に存在するため、半素数も無数に存在することになります。ちなみに最小の半素数は4(2×2)ですし、先ほど取り上げた来年の西暦である2019も(3×673)で半素数です。
最後に、今日取り上げた1234321と1234567の2つの数について、数字の並びをそのままにして、加減乗除等の記号を入れて、今日の日にち11月27日の数字をそのまま並べた1127を作ることに挑戦してみます。
12!!!-(3!)!-(4!!)!!!-(3!)!!!+2-1=1127 → 11月27日
1234-5!+6+7=1127 → 11月27日
*「半素数」について
名前がついているぐらいだから、数学、特に暗号化理論の分野では研究の対象になっています。ここでは極々簡単に。
インターネットでやり取りするデータは、常に悪質な第3者に傍受されているという前提で利用しなければなりません。クレジットカードの番号を入力するとき、その番号が盗まれて第三者に不正に使われないかとか心配したことがある人も多いはずです。
そこで、たとえ盗まれても絶対に読まれないように、データを暗号化する必要があります。その時にデータに素数を使った「鍵」を掛けます。2個の素数の積を求めることは簡単ですが、半素数を素因数分解して元の2個の素数を求めることは、その桁が大きくなればなるほど困難であり、そのことが「鍵」の安全性の原理になっています。事実、わずか7桁の数である1234567も127×9721のように素因数分解に苦戦しました。
図書館にある雑誌Newtonの昨年8月号が「素数の神秘」という特集を組んでいて、そこに素数を使った「鍵」について分かりやすく解説してあります。興味がある方は是非ご一読を。
追伸
1234567で思い出しました。123456789人です。何の数字でしょう?
昔、私が駆け出しの教員だった頃、新聞の見出しにこうありました。「日本の人口、今日123456789人」
いつの頃だったのかと改めてネットで調べたら、平成2年(1990年)4月3日のようです。ずっと増加傾向だった日本の総人口は、平成16年(2004年)12月の1億2783万8000人をピーク(総務省発表)に減少に転じています。減少のサイクルに入った日本の人口が再び123456789と並ぶのは2020年頃だと言われています。私たちはそのことを報じるニュースをどう受け止めるのでしょうか?
【校長】
手巻きウインチの設計図面がこんな形で!
いつも本校のHPにお越しいただきありがとうございます。
今日、学校は球磨工フェスタ(文化祭)を開催しています。あいにく、人吉市は産業祭を行っており、地域の中学校も文化祭をしているそうです。出足が心配されましたが、天気に恵まれたこともありお陰様で大盛況です。でも、中学生の皆さんにご観覧いただくことができなかったことは残念に思います。

私は昔、機械科の教師をしていました。前々々任校のことになりますが、3年間の機械科での学習の総まとめとして、卒業製図と称して描かせていたのがこの図面です。寒さに震えながら夜遅くまで描いていた生徒たちのことを思い出しました。
誰が描いた図面か知るよしもありませんが、将来こういう形で文化祭のポスターとして裏面が甦(よみがえ)るとはまさか思わなかったはずです。ある意味、機械科らしい究極のエコかもしれません。
話は変わりますが、体育館で行われた午前の部が終わり、校長室に戻りHPを開けたところ、今、午前11時24分現在の総アクセス件数は、1219957。
今日11月11日の日にちの数字の並びは1111で、レピュニット数(1がいくつも並んだ数字のこと。repunit【repeated unitの略】)です。
ということで、いつものように1219957に加減乗除等の記号を入れて、この1111を作ってみます。
121×9+√9×5+7=1111 → 11月11日
あまりにも簡単に出来たので手応えを感じません。もう一つ作ってみます。
√121+995+7!!=1111 → 11月11日
いくつも出来そうな気がします。皆さんだったらどんな式を作りますか?
【校長】
今日は古典の日

写真は一昨日、多良木高校であった会議に行った際に目にした校庭の木々をパシャリしたものです。さすがは奥球磨、人吉市内より色づくのが早いように思いました。
ところで、11月1日は「古典の日」。源氏物語千年紀を記念して10年前の平成20年(2008年)11月1日に京都で宣言されました。何とその2年後の平成22年、国の法律でも制定されました。
「こういうことが法律になじむのか?」と思えるような興味深い法律です。法文を読んだことがある方はきっと少ないでしょうから、全文を引用して紹介します。
(目的)
第一条 この法律は、古典が、我が国の文化において重要な位置を占め、優れた価値を有していることに鑑み、古典の日を設けること等により、様々な場において、国民が古典に親しむことを促し、その心のよりどころとして古典を広く根づかせ、もって心豊かな国民生活及び文化的で活力ある社会の実現に寄与することを目的とする。
(定義)
第二条 この法律において「古典」とは、文学、音楽、美術、演劇、伝統芸能、演芸、生活文化その他の文化芸術、学術又は思想の分野における古来の文化的所産であって、我が国において創造され、又は継承され、国民に多くの恵沢をもたらすものとして、優れた価値を有すると認められるに至ったものをいう。
(古典の日)
第三条 国民の間に広く古典についての関心と理解を深めるようにするため、古典の日を設ける。
2 古典の日は、十一月一日とする。
3 国及び地方公共団体は、古典の日には、その趣旨にふさわしい行事が実施されるよ う努めるものとする。
4 国及び地方公共団体は、前項に規定するもののほか、家庭、学校、職場、地域その他の様々な場において、国民が古典に親しむことができるよう、古典に関する学習及び古典を活用した教育の機会の整備、古典に関する調査研究の推進及びその成果の普及その他の必要な施策を講ずるよう努めるものとする。
附 則
この法律は、公布の日から施行する。
6年前、「古典の日」が法律で制定された時、マスコミでも大きく取り上げられました。当時、「えっ!何でまた法律で・・・?」と、私自身はかなり複雑な思いで受け止めたことを思い出します。
というのも、そもそも「古典の日」が京都で宣言された発端が、源氏物語の執筆千年を記念したものだったので、この法律でいう「古典」とはいわゆる国語で習う(文学の)古典とばかり思い込んでしまったからです。高校のとき、「ラ行変格活用」などでアトピーが出るほど苦しんだ古語文法を思い出し、「国は何と嫌な日を作ってくれたんだ!?」と思ってしまったわけです。
それから数年後、どういういきさつだったか忘れましたが、条文に目を通す機会がありました。第二条の「古典」の定義によると、文学だけでなく音楽や美術、演劇・・・と様々であり、「なんだ、そういうことだったんだ・・・(安堵)」と思った次第でした。
定義の後段には、「学術」や「思想」という言葉も出てきます。その視点から考えを巡らせてみると、今皆さん方が少なくとも普通教科で習っていることのほとんど、数学のサイン・コサインにしろ、理科のアボガドロ数にしろ、現社で学ぶベンサムの功利主義にしろ・・・、人類の叡智(えいち)の結晶であり、まさに古典といってもいいですよね。
私、そういうことも踏まえて、入学式の式辞に「古典」のことも触れることにし、毎年次のように話をしています。抜き出しておきますので、文中の「いにしえの賢人の思想」に着目しながら入学式の日を思い出してください。「そんな話、聞いたかな・・・」と思う人がいるかも?
・・・(前略)・・・第四次産業革命が社会や生活を大きく変えようとしている今、知識を得ることは勿論ですが、将来の技術者・技能者として数学的・論理的なものの見方や考え方をしっかり身に付けることは必要不可欠です。さらに、異文化やいにしえの賢人の思想に触れることで、自分の心の幅を広げ、それらを基に自分自身の頭で考え、判断し、実行する力も求められます。その意味で、中学までの教師や親から言われてする勉強から脱却し、知的好奇心を持って自ら学ぶ力を身に付けなければなりません。三綱領の中にある好学とはまさにそのような姿勢です。・・・(後略)・・・
話を大きく変えます。古典の日である今日11月1日に思いを込めて、朝一番(7時25分)にHPを開けた時の総アクセス数である1209199に加減乗除等の記号を入れて、日にちの数字の並びである111を作ってみます。
(120-9)×1(9-9)=111 → 11月1日
あっという間に式ができて拍子抜けです。生徒の皆さんだったらどんな式を作りますか?
【校長】
【注】 中学生の皆さんへ
102=10×10=100 とか 23=2×2×2=8 は御存じのとおりです。高校の数学では、もっとすごいものが出てきます。上に小さく書く数字を「指数」と呼びますが、この指数が0やマイナスのものが出てくるのです。
例えば、50とか、2-2という形のものです。
「0乗ってナニ?」「-2乗って・・・!?」
初めて見る人は、そう思うかもしれません。
それから、なんとこの指数、整数にとどまらず、有理数(二つの整数 a, b (ただしbは0 でない)をもちいて a/b という分数で表せる数)になることもあります。
64(2/3) とかです。3分の2乗とか、もう本当にすごい世界です。このように数の世界が広がることを「指数の拡張」と言うことがあります。
ちなみに、50は1、2-2は0.25、64(2/3)は16になります。
「・・・何で(?_?)」というのが実感かもしれませんが、高校の数学をお楽しみに。
ということで、今日の式の指数にあった(9-9)は0であり、1の0乗は1であることに注意しながら味わってください。
このように、どんな数も0乗すると1になります。今はそう覚えておいてください。勿論、高校ではなぜ0乗が1になるのか説明できるようになるはずです。
最後に・・・、今、「どんな数も・・・」と書きましたが、00(0の0乗)については、「0に0をかけると0だが、0の0乗は1である。果たして??」といった議論になることがあります。このことを理解するためには、高校の数学も越える高度な数学の素養が必要かもしれません。
祝 総アクセス数 120万件達成
いつも本校のHPにお越しいただき、ありがとうございます。
10月に入り、1日当たり平均1100件のアクセスをいただきながらカウンターは順調に数を伸ばしていました。

百二十万! 久々にきりのいい数字です。こういう綺麗な数字を見ると無性に素因数分解をしてみたくなります。早々やってみます。
1200000=27×3×55
従って、その約数は、1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 25, 30, 32, 40, 48, 50, 60, 64, 75, 80, 96, 100, 120, 125, 128, 150, 160, 192, 200, 240, 250, 300, 320, 375, 384, 400, 480, 500, 600, 625, 640, 750, 800, 960, 1000, 1200, 1250, ・・・(途中省略)・・・, 60000, 75000, 80000, 100000, 120000, 150000, 200000, 240000, 300000, 400000, 600000, 1200000
の96個あることになります。
では、いつものように 1200000 という数字の並びをそのままにして、加減乗除等の記号を入れて、今日の日にち10月24日の数字をそのまま並べた1024を作ることに挑戦してみます。
1×2(0!+0!+0!+0!+0!)!!!=1024
【注】 中学生の皆さんへ。”!”は、高校で学習する内容ですので、こうやって何度も説明していますが、”!”は「階乗」または「ファクトリアル」と読みます。
例えば5!なら、5×4×3×2×1を計算して120になります。
そして、0!=1というのも知っておく必要があります。これは定義(決めごと)ですから「どうしてそうなるの?」なんて考えたらいけません。
そういうことで、指数部にある(0!+0!+0!+0!+0!)の結果が5になる所までは大丈夫だと思います。
問題は”!!!”です。これは「3重階乗」といいます。このことについては、昨年の8月2日の記事以来、何度か解説していますが、このような「多重階乗」は、高校の数学の範囲も超えますので、「2重階乗(ダブルファクトリアル)」や「3重階乗(トリプルファクトリアル)」から順を追ってもう一度おさらいをしておきます。決して難しいものではありません。ついて来てください。
・まず、2重階乗(!!)は階乗の1つ飛ばしバージョンと考えてください。
n!!なら、n×(n-2)×(n-4)×・・・×・・・というように、2つずつ減らしながら掛け合わせます。nが偶数だと×4×2で終わりますが、nが奇数だと最後は×3×1で終わることになります。5を例にとってやると
5!!=5×3×1=15 となります。
・3重階乗(!!!)は階乗の2つ飛ばしバージョンと考えてください。
従って、5!!!なら、2つおきの階乗ですから、5×2で10になります。
要は、210=1024 を作ったわけです。2を10回かけると1024、これはとても有名であり、覚えておいて損はありません。
ちなみに、高校に入学して1年もしくは2年生で学習する専門の基礎科目に情報技術基礎という科目があります。その中にコンピュータで用いられる単位であるビットとバイトを扱う単元があり、この1024という数字が登場します。
コンピュータでは、2進数を扱う都合からキロ(K)やメガ(M)といった接頭辞が1000ではなく1024のべき乗で表示します。例えば、1 KB=1024 B、1 MB =1024 KB となります。つまり、1024Bが1kB、1024KBが1MB、1024MBが1GB、1024GBが1TB・・・となります。
簡単に言いますと、2進法で表すコンピュータの世界での1つの単位の大きさは、1024倍ごとに上がっていきます。高校の授業をお楽しみに・・・
ということで、「毎月120万円のお給料があれば(経済的には)幸せだろうな・・・」なんて思いつつ、あくまでも仮定の妄想をしながらこの数字と遊んでみました。
【校長】
「よけまん」って?
いつも本校のホームページにお越しいただきありがとうございます。

生徒の皆さん、頑張ってください。
ところで、学校からちょっと郊外に足を向けてみると、球磨川沿いに広がる田んぼでは、稲の穂が重そうに垂れています。
秋まさにたけなわ。
この光景を見ていると、「実るほど頭を垂れる稲穂かな」という言葉を思い出しました。色々な話でよく引用されますので、きっと生徒の皆さんも聞いたことがあると思います。稲の穂は実るほどに穂先が低く下がるわけですが、人も社会的な立場が高くなればなるほど、謙虚な姿勢で人と接することが大切であるという教えです。(私自身はこの言葉、パナソニックの創業者松下幸之助氏の「人生談義」という本の中で知りました)
稲と言えば・・・
お隣の高校、南稜高校のHPの昨日の記事が印象的でした。「南稜米の調製が終わりました!」というタイトルのブログの中に、調製作業が終わった南稜米を冷蔵庫へ運ぶ様子が写真付きで載っていました。今年は豊作だそうです。お米が一杯に詰まった100袋もの米袋をトラックから冷蔵庫まで運ぶのは、本当に大変だったみたいです。実際、とても難儀そうに運んでいて、袋を担ぐ生徒の表情に重さが滲み出ていました。
その記事の中に気になる言葉を見つけました! 次の一文です。
「重い、重い」と言いながら持ち方を工夫して運びました。終わった後、「よけまんがあればいいのに」と。確かに(笑)
私、「よけまん」という言葉を初めて目にしました。何人かの先生に聞いたところ御存じないようでしたので、「きっと方言に違いない!」と思って検索してみました。
やっぱりそうでした。あるサイトに、次のように紹介されていました。
この言葉の意味を知ってる方は、相当ディープな熊本人か、熊本オタクですね!「よけまん」とは、主に球磨地方に伝わる方言で、おやつ とか、一息入れる という意味です。よける(避ける) と おまんま がくっついて、「よけまん」となったそうで、「田んぼや畑での農作業を休憩して、おやつで一息いれる」という、意味合いなんだそうです。でも、昔むかしの言葉ではなく、球磨では今も立派に、普通に使われてるんですよ。・・・(後略)・・・
ディープな熊本人とか熊本オタクというコメントが何とも面白く可笑しいです。
それはさておき、農業系の高校は血が通う生き物を相手にしているので、工業高校とはまた違った学校の日常があり、ブログの内容もバラエティに富んでいます。同じ高校生として、隣の高校に通う友がどのようなことを学んでいるのか、他校のHPもちょっとのぞいてみてはいかがでしょうか。
【校長】
待ちなんかった 青井さん
昨日の青井阿蘇神社のおくんち祭りに参加した生徒の皆さん、大変お疲れ様でした。
陵和会(同窓会)の神輿(みこし)を担ぎたいと自ら手を挙げた3年生は今年101人であり、平成23年に生徒が参加し始めて以来最多の人数だったと担当の先生から伺いました。祭り好きの人にとっては、待ちなんかったことでしょう。

特に、最後の宮入行事、なかなか神輿を神前に納めさせてもらえず「セイヤ・セイヤ」の勇ましいかけ声を境内いっぱいに響き渡らせながら何度も繰り返しになり、見ていて圧巻でした。担ぐほうは超大変だったのでは?鈴の音も大きく鳴り響き、きっと青井の神様も喜ばれたのではないかと思っています。

話は変わりますが、今日10月10日は以前「体育の日」でした。1964年10月10日の東京オリンピックの開会式が行われたこの日、真っ青な大空に自衛隊機が五輪の大円のジェット雲を描く様子は繰り返し放映されていますので、見たことがある人は多いはずです。この日、東京の空は雲一つない快晴だったそうです。統計上晴れの日が多い「晴れの特異日*」に開会式をもってきたとか(嘘か本当か知りませんが)聞いたことがあります。
しかし、ここ人吉は昨日と一変して曇天(午後の降水確率60%)です。特異日が現れる気象学的原因はまだ解明されていないそうですが、閏年とかあるのになぜ毎年同じ日になるのか昔から不思議に思っています。
今日は、そんな10月10日に思いを込めて、今朝7時30分現在のHPの総アクセス数1184473を使って久々に数遊びをしてみたくなりました。数字の並びをそのままにして、加減乗除等の記号を入れ、今日10月10日の「1010」という数字を作ることします。(お昼休みの楽しみにとっておきました)
11!!!+8!!!+4!×√4+√(7-3)=1010→10月10日
特に手こずることなく、10分ほどで完了です。あまりにも簡単でしたから、もう一つ挑戦することにします。

青井阿蘇神社が球磨盆地のほぼ中央部、球磨川北側のあの地に鎮座して1212年目ということでしょう。
この1212というのも印象的でいい数字だと思います。そこで、この1212という数字を、同じく1184473から作ってみることにします。
1184+4!+7-3=1212
これまた簡単にできて、拍子抜けでした。皆さんだったらどのような式を作りますか?
【注】 中学生の皆さんへ。もう何度も説明していますが、”!”は「階乗」または「ファクトリアル」と読み、例えば4なら、4×3×2×1を計算して24になります。
・これに対して、2重階乗(!!)は階乗の1つ飛ばしバージョンと考えてください。
n!!なら、n×(n-2)×(n-4)×・・・×・・・というように、2つずつ減らしながら掛け合わせます。nが偶数だと×4×2で終わりますが、nが奇数だと最後は✕3✕1で終わることになります。
・3重階乗は階乗の2つ飛ばしバージョンです。n!!!なら、n×(n-3)×(n-6)×・・・ということです。最後は最小自然数まで掛けることになります。
従って、 8!!!=8×5×2=80
11!!!=11×8×5×2=880 となります。
* 特異日については、ネット上のコトバンクに次のように解説してありました。
長年にわたって毎日の気象状態の平均をとったとき、特定の日にある気象状態が偶然とは考えられないほど大きな確率で出現し、かつその前後の日にはそれほど大きくない出現確率のとき、この日を特異日(singularity)と呼ぶ。日本では 1月16日および 3月14日の「晴れ」、4月3日の「春の荒れ」、4月6日の「寒の戻り」、6月11日の「入梅」、9月17日および 26日の「台風来襲」、11月3日の「秋晴れ」などがよく知られる。
【校長】
今日は資格チャレンジの日
いつも本校のHPにお越しいただきありがとうございます。

近隣の高校が早々と延期を決める中、漏れ伝わってくる3年生のこの大会に懸ける意気込みにどう応えるか、最終的な判断をする者としてギリギリまで悩みました。
万一ぬかるんだグラウンドで足を取られ、骨折等大きな怪我があったり、気温が低い中、低体温症で救急車の出動があったりしたら・・・・色々なケースも考えました。最終的には、批判が出ることは重々承知で実施を決断しました。
集団演技の時に雨が上がったのは奇跡的で、大袈裟ですが「天の恩寵」だと思いました。「沢山の観客の前で演技ができてよかった」という生徒たちの声も聞き、時間短縮・種目変更・・・色々ありはしましたが、結果的には事故・怪我なく終わり、明日に延期してやるより雨天の中、かえって引き締まったのではないかと思っています。
一昨日夜、保護者の皆様にもこの気持ちをメールで配信したところです。保護者の皆様には、御理解・御協力をいただき誠にありがとうございました。

今朝のテレビのニュースは台風関連ばかりでしたが、ラジオでは今日は「日本酒の日」と言っていました。聞くところによると、10月に入ると新米の収穫が始まり、全国各地の蔵が日本酒造りを始めるからだそうです。鉄チャンの私としては、今日は東海道新幹線が開業した日(1964年)というのが真っ先に思い浮かびました。10月1日は「衣替え」でもあります。今朝の官舎の台所は21℃で肌寒かったので、冬に向けての準備をしなければならないと実感したところでした。
そういうことで、10月1日は各種団体が独自に定めた記念日が何かしら多そうな感じがして、ちょっと調べてみました。沢山ありました。
国際高齢者デー、コーヒーの日、法の日、日本茶の日、日本酒の日、メガネの日、・・・(途中略)・・・トンカツの日、雨といの日、ポイントカードの日、資格チャレンジの日、釜飯の日、あずきの日、省エネルギーの日・・・(以下略)・・・
何と47個も羅列されていました。それぞれのいわれを読んでいたら、無理な語呂合わせも多く、なかなか面白いと思ったところです。気になるのは「資格チャレンジの日」です。本校でも皆さんに資格取得を推奨しているからです。なぜ今日なの?と、想像を巡らせました。
制定・登録した一般社団法人日本記念日協会によると、「自己啓発・転職・就職などで重要な資格とその取得について、毎月の初日である1日に考え、資格取得への挑戦を促進し、より良き人生を目指してもらうことが目的」とありました。確かに、月の初日というのは気分一新、新しいことにチャレンジするにはうってつけかもしれません。
今日の職員朝会では、危険物取扱者の試験が12月8日(土)に本校で行われることが決定したという連絡がありました。この試験、全国的な合格率が低下して難化の傾向にあります。昨年度の本校生の合格率も今一つで、パッとしませんでした。リベンジをかけようと思っている人は多いはずです。
危険物はその取り扱いを誤り万一事故が発生すれば、人命を危険にさらし、環境を汚染し、地域社会に大きな被害を与え、企業は莫大な損害を被り大きな責任を負うことになります。その元々の原因は、あり得ないようなちょっとした判断ミスが多いと聞いています。今の皆さんにとっては、スキルアップの資格かもしれませんが、安全な社会づくりの使命を帯びた資格であるということもしっかり自覚して、計画を立てて頑張ってください。
ということで、1年365日すべてに何かしらの記念日があり、その数の多さに改めて驚かされたわけですが、最も記念日の多い日はいつなのかということも気になり調べてみました。何と10日後、10月10日みたいです。
【校長】
気を揉む台風24号の動き
いつも本校のHPにお越しいただきありがとうございます。

詳細は専攻科からアップされていたブログのとおりですが、祠を積んだトラックの後ろをつけて、昼過ぎに現場に到着しました。
右の写真では分かりにくいかもしれませんが、道路から設置場所までの通路が意外に狭く、フォークリフトや小型クレーン車を使って難儀しながら少しずつ移動させ、3時半頃やっと設置作業に取りかかることができました。あいにく秋の冷たい雨がぱらつく中での作業になりました。それにもかかわらず、地元の氏子さんたちも20名ほど出て来られ、笑顔で作業の様子を見守っていただきました。ありがとうございました。
ところで、今日は昨日の雨でぬかるんだグラウンドを整地しながら、体育大会の予行があっています。そんな生徒・職員みんなが気を揉んでいるのは天気のことです。遥か南の海を北上中の台風24号が、九州から本州にかけて停滞している秋雨前線を刺激しているようです。大会当日は雨、しかも予備日としている30日(日)は暴風雨のようです。少々の雨でも当初の予定通り29日(土)に実施するか、それとも来週の2日(火)とかに延期するか、難しい判断を迫られています。明日(28日)のお昼には態度決定をしてHP上でお知らせします。
最後に・・・
先週水曜日(9月19日)にアップしていた「サギと三角形の面積」の記事の中で「面積が24になる三角形の3辺がヘロン数として見つかったら教えてください」と書いていましたが、本校電気科の仲嶺先生の御親友から「2組見つかったよ」とメールをいただきました。お知らせいただきありがとうございました。
(a, b, c)= (6,8,10)→面積=24 (4,13,15)→面積=24
三辺が500までの自然数について、何とエクセルを使って計算させた結果なんだそうです。
よ~く見るまでもなく、このうち6,8,10は、三平方の定理で有名な辺の比が3:4:5の直角三角形ですよね。私、ピタゴラス数*はいつもヘロン数になるという至極当たり前のことを忘れていました。
そして、この(6,8,10)の三角形は、辺の長さの和と面積がいずれも24になります。今とても気を揉んでいる台風も24号と同じ数字でもあり、何か変な縁を感じます。
* ピタゴラス数とは、直角三角形において、三平方の定理 a2 + b2 = c2を成り立たせる自然数の組のことです。よく知られているのは、(a,b,c)=(3,4,5)、(5,12,13)などでしょうか。
このピタゴラス数は、c<100の範囲で次の16個あることが知られているそうです。意外に沢山あることに改めて驚いたところですが、数学の先生だったら「作問に使えるな・・・」と思うかもしれません。
(a,b,c)=(3,4,5)、(5,12,13)、(15,8,17)、(7,24,25)、(21,20,29)、(9,40,41)、
(35,12,37)、(11,60,61)、(45,28,53)、(33,56,65)、(13,84,85)、(63,16,65)、
(55,48,73)、(39,80,89)、(77,36,85)、(65,72,97)
【校長】
サギと三角形の面積
いつも本校のHPにお越しいただきありがとうございます。
先週金曜日から始まった体育大会の練習、3連休を挟んで3日目になる今日は、1年生が午前中体育館で集団演技の練習をしました。いかがでしょうか。練習を通して、少しずつ形が出来上がっていることを実感していますか?

サギにはいい思い出があります。昔、釣にはまっていた時のことです。川岸で釣をしていたら、サギからずっと背後で待たれていたことがあります。つり上げた魚を貰おうとしているのです。そのような光景、時々新聞写真等で紹介されますので、イメージが湧く方が多いかもしれません。まさか自分がその当事者になるとは・・・! とても光栄でした。
魚を釣っているということをしっかり理解し、辛抱強く待つ様子からは知能の高さが窺えます。サギ君に魚をあげようと、ついつい粘ってしまい、これもまた釣の一つの醍醐味と言ってもいいかもしれないな、とか思ったところでした。鳥は警戒心が強いというのが私の認識でしたので、野生のサギがこんなに人間と接する生き物とは本当に驚きです。
古来、日本人とサギは親しい関係だったのかもしれません。それを裏付けることとして、温泉の開湯伝説を思い出します。「日本三古湯」の一つ、愛媛県・道後温泉に伝わる「足に傷を負って苦しんでいた一羽の白鷺が、岩間から噴出する温泉を見つけた」という話を聞いたことがある人は多いはずです。このように歴史ある温泉には開湯伝説があり、そこには鹿や熊などの動物が登場することがあるのですが、一番多いのが「白鷺伝説」なんだそうです。
改めてネットで「温泉 サギ」と入れて検索してみると沢山ヒットし、サギが温泉で脚の傷を治したという話は定番になっていることが窺えます。それにしても、あんな堅そうな脚ではお湯の温かさも感じられないのでは?と思うのですが、血管は通っているはずなので、長く湯に入っていれば多少は体も温まるのかもしれません。私が初任や前任校のころによく通った武雄温泉(佐賀)や天草下田温泉も白鷺伝説があります。人吉市内にも「白鷺の湯」という温泉がありますよね。
話は変わりますが、生徒の皆さんはサギを英語で何というか知っていますか?
答はheron(ヘロン)です。
何と、三角形の3辺の長さから素早く面積を求める公式を発見した古代エジプトの数学者・技術者のヘロン(Heron)さんと綴りが一緒です!
2、3年生は数学の教科書の中に見受けた人もいると思いますが、ヘロンの公式を発見した人として有名です。その公式とは、三角形の3辺の長さをa,b,cとしたとき、面積を次の式で求めるものです。
三角形の面積=√{s(s-a)(s-b)(s-c)}
ただし、s=(a+b+c)/2
私がヘロンの公式を初めて目にしたのは、中学1年生の時でした。図書館から借りた数学史の本の中に見つけました。当時、三角形の面積を求める公式は「(底辺)×(高さ)÷2」しか知らなかった私にとって、3辺の長さからそれを求めることができるというのは大変な驚きで、しかもその公式が遥か2000年も前の紀元前1世紀に発見されていたということを知り衝撃的でもありました。三角関数(三角比)を使わずに中学生でも理解できる証明が載っていて、理解をしようと、もがきまくった覚えがあります。
当時、この公式を使って、あることに挑戦したことも懐かしく思い出します。何かというと、三角形の3辺とも長さが自然数で、かつ面積も自然数となるような3辺を見つけることです。結構時間を費やしたはずですが、結局その当時見つけることができませんでした。随分後になって、そういう三角形は「ヘロン三角形」と名付けられ、3辺の長さの三つ組(a,b,c)をヘロン数と呼ぶことなどを知りました。例えば(13,14,15)はヘロン数(面積は84)です。
今朝の7時35分現在の本校の総アクセス数は1159305でした。この数字、各桁の数の総和(1+1+5+9+3+0+5)を求めると何と「24」。
私の名前(西)の擬音語(オノマトペ)の数字表現である「24」と偶然同じです。そして今話題にしている「サギ」の漢字「鷺」も総画数24画です。凄い偶然を感じます。ということで、中学の時に挑戦したことを再びやってみようという気になりました。
即ち、サギにあやかって、面積が24になる三角形の3辺がヘロン数として存在するか見つけようというものです。生徒の皆さん方の体育大会の練習を眺めながら、数時間色々な数字で試してみましたが結局、見つけることができませんでした。
生徒の皆さんで、もし見つかったら教えてください。ただし、存在しないことを証明しようとすると、数学界ではすぐ難問になりますので要注意です。
【校長】
18と秋の到来
夏休みも残り1週間を切りました。焦っている人がいるかもしれません。
本校のホームページ、たまたま開いた昨夜8月26日の20時13分現在の総アクセス数は1142052でした。
この数字をずっと見ていたら、面白いことに気付きました。下4桁の2052と上3桁の114との関係です。
何と、2052÷114=18ということで、綺麗に割り切れるのです。たまたま目にした数字で、このことに気付き、当夜の満月も相まって「吉兆」を感じたところでした。
この18という数字、西洋では「悪魔の数字」とされる666との関係(6+6+6=18など)がよく取り沙汰されますが、私にとっては小中学校の時に何度か出席番号でお世話になったこともある思い出深い数の1つです。
18といえば、相良33観音巡りで相良村川辺にある18番札所「廻(めぐ)り観音」につい3日前、熊本出張から五木越えで帰る途中に立ち寄ったばかりでした。すぐ横の川辺川が激流のようになっていて、鮎釣りをする人が流されないかと気を揉みました。

そんなことを思い出していたら、「百人一首の18番の歌は何だったかな?」と気になりました。(教諭のころ、百人一首部の顧問をしていました)
調べてみたら、「住の江の岸に寄る波よるさへや・・・」で、平安時代の藤原俊行の歌です。
藤原俊行といったら、この歌よりも中学校の時の国語で習った
私は、枯れて元気を失ったひまわりの大輪が頭を下げて茶色く変色しつつあるのを見て、「しっかりしてよ、ひまわり君!」とか言いながら夏の終わりを感じました。
【校長】
残暑お見舞い申し上げます

夏休みもいよいよ折り返し。宿題が気になり始めた人がいるかもしれません。計画を立ててお過ごしください。
この間も、3年生は連日登校して、SPI対策、履歴書の清書等に懸命に取り組んでいますし、1,2年生は暑い中、さらに暑い体育館等で練習に明け暮れています。
先ほどは、8月3日(金)から6日(月)にかけて、岐阜県海津市長良川国際レガッタコースで開催されたインターハイ・カヌー競技に出場した選手7名が顧問の中島先生と共に結果の報告に来室しました。カナディアンペア500mが準決勝3位、カナディアンフォアが5位入賞ということでした。県の青のユニフォームを着て、真っ黒に日焼けした姿が凜々しかったです。おめでとうございます。
話は変わりますが、明日11日は新月です。何か目標を達成しようと思うとき、人はその達成を強く願うものですが、その最もよいタイミングが新月の日だとされています。2学期がうまくスタートできるように、月に願いを込めてみてはいかがでしょうか。
【校長】
全校応援、お世話になりました。
いつも本校のHPにお越しいただきありがとうございます。
昨日は全校応援でした。炎天下、第4シードの有明高校との試合は、天候と同じく熱いものとなりました。
生徒の皆さんの気迫のこもった応援が選手の背中を押したのでしょう。白熱した息詰まる接戦を制して、2対0で勝利。校歌を高らかに歌うことができ、胸が高まりました。
そして・・・、胸をなで下ろしたこともあります。昨日の試合では全部で34人が熱中症の疑いで救急搬送されたそうですが、本校からは救急車に乗った生徒が一人もいなかったということです。体育や部活での日頃の身体の鍛え方が本物であることを証明したようなものです。三綱領にある「剛健」がしっかり身についていています!
「人吉球磨から甲子園に」の悲願達成のためには、あと2回勝ち続けなければなりません。引き続き応援をお願いします。
ただ、県高野連からは全校応援の自粛要請がありました。そこで、21日(土)の準決勝については、せっかく応援計画を立てていましたが、全校応援は急遽見合わせることにしました。
希望者が自主的に藤崎台球場に応援に行くことを妨げるものではありませんが、熱中症が心配されます。テレビ等を通しての応援でも「祈り」は通じるはずです。できましたらその方向での協力を宜しくお願いします。
最後に・・・。3日前の熊本高校と本校の試合は7回裏の時点で、8対1で7点差のコールドゲームで勝利しました。


(一昨日の記事はこちらをクリック→総アクセス数1111111と7月17日と239)
そんなゲームがあれば「どういう試合運びだったらそういうことが起こるのか・・・」と想像が広がり楽しかったです。
【校長】
総アクセス数1111111と7月17日と239
いつも本校のHPにお越しいただきありがとうございます。

改めて蝉時雨の意味を手元の辞書で確認したところ、「たくさんの蝉が鳴いているさまを時雨の降る音にたとえていう語」(時雨は「初冬の頃、一時、風が強まり、急にぱらぱらと降ってはやみ、数時間で通り過ぎてゆく雨)とありました。夏生まれの私にとっても、朝から蝉時雨を聞きながら目が覚めるのは幸せなひと時ですが、「死ぬほど」という表現が可笑しく、この季節になるとその友のことを思い出します。
生徒の皆さんは、死ぬほど好きな日本語ってありますか?私自身、好きな言葉なら「木漏れ日」や「恩寵(おんちょう)」、「逢瀬」、「春うらら」*1等、ぱっと思いつきますが、「死ぬほど・・・」と言われると、はて何だろうと考え込んでしまいます。

「レビュニット」というのは、ほとんどの生徒の皆さんにとって初めて耳にする言葉かもしれません。この数字もそうですが、111や11111のように1がいくつも並んだ数字を「レピュニット」(repunit【repeated unitの略】)といいます。そして、素数であるレピュニットは「レピュニット(型の)素数」と呼ばれ、あるレピュニットが素数であるかどうかというのが、例によって素数ファンの関心事*2になっています。
この1111111は、レピュニット素数でしょうか?さっそく素因数分解ができないか確かめてみます。
色々な素数で割ってみました。なかなか素因数が見つかりません。根負けしてネット上の素数判定機にかけてみたら、素数ではありませんでした。1が7連続するこの数からは想像すらできない、意外に大きな2つの素数の積になっていました。
1111111=239×4649
従って、約数は1,239,4649,1111111の4個あることになります。
4649という素因数が何ともいいですね。「よろしく」と読めます。人吉から熊本まで国道219号線を2時間運転すると、このナンバーをつけたクルマと1台はすれ違っている気がします。でも、希望ナンバー制の人気ベスト200のランキングには入っていませんでした。
そしてもう一つの素因数239も・・・。
私はこのことにたった今気付き、あまりの偶然に恐れおののいているところです。今日7月17日の数字の並びである717を素因数分解すると
717=3×239でした。ここにも239が隠れていたとは!?
ということで、1111111の数字の並びをそのままにして、加減乗除等の記号を入れて、717を作ってみたくもなりました。
{(1+1+1)!}!-(1-1)!-1-1=717 → 7月17日
【注】 中学生の皆さんへ !は「階乗」または「ファクトリアル」と読み、詳しいことは高校の数学で学習しますが、例えばここに出てくる3!なら3×2×1を計算して6ですし、ここではさらにその6の階乗を求めています。6!=6×5×4×3×2×1ですから720になります。このようにn!なら、n×(n-1)×…×3×2×1の自然数の積を計算します。
そして、(1-1)!は0!のことです。0!(ゼロの階乗)は1です。これは約束(決め事)ですから、「どうしてそうなるの?」とか考えたらいけません。
最後に1111111に関する頭の体操を3問出題します。生徒の皆さん、よかったら解いてみてください。
① 1111111が2進数だとしたら、これは10進数ではいくらでしょう?
② 1+11+111+1111+11111+111111+1111111=?
③ 11111112の計算結果は?(なるべくエレガントに計算してください)
答え
① 127
② 1234567
③ 1234567654321
略解
① 1×26+1×25+1×24+1×23+1×22+1×21+1×20
=64+32+16+8+4+2+1
=127
これは情報技術検定3級のレベルです。2進数を日常的に扱うコンピューターのシステムエンジニア(SE)にとっては、すぐに127と反応できないと飯を食べていけない・・・とか聞いたことがあります。
② 1
+ 11
+ 111
+ 1111
+ 11111
+ 111111
+ 1111111
= 1234567
③ 11111112
=1111111×1111111
=1111111×(1000000+100000+10000+1000+100+10+1)
= 1111111000000
+ 111111100000
+ 11111110000
+ 1111111000
+ 111111100
+ 11111110
+ 1111111
= 1234567654321

時々耳にする恩寵、奥深い言葉です。神が人間に与える恵み、神の無償の賜物(たまもの)のことです。村上春樹の小説の多くは、恩寵が深い所でテーマなっているようで、そのことを意識しだすと頭が混乱します。
「契りを結ぶ」は古典では必須の言葉ですよね。現代において、「約束する」という堅い意味で使われることはあまりないように思うのですが、そういう文字通りの意味があるからこそ、恋愛についてのくだりでは意味するところが明らかなのに、刺激的な匂いを感じさせない言葉だと思っています。
「春うらら」は漢字では「春麗」とありました。「春のうららの隅田川~♪」(by滝廉太郎)は、文部省唱歌として中学校の時に習いましたが、文科省唱歌と名を変えて今でも指導しているんでしょうか?
*21が並んでいる数はいかにも素数っぽいのですが、レピュニット素数は意外に稀のようです。11の次のレピュニット素数は1が19個並ぶまで現れず、その次は23個。その次は飛んで317個。その次はさらに飛んで1031個の時だそうです。
レビュニット素数がどんなタイミングで出現するのか、あるいは無限に存在するかどうかというのは未解決問題となっており、好事家たちの関心を引くのもわかるような気がします。
【校長】
梅雨明け
いつも本校のHPにお越しいただきありありがとうございます。

※ 右の写真は、昨日(10日)の夕方5時頃、本校の上に出現した虹です。最近虹をよく見ます。確か、この一ヶ月で4回目(内1回は月夜の虹でした)。飛行機から見ると、遮るモノが無いので丸く見えるとか聞いたことがあります。本当かなぁ?
今日は昼から熊本市内で研修会でした。途中の休憩時間に野球の試合結果が入り(対御船高校戦、6対0で勝利)、回りの先生方から祝福の言葉を頂きました。
その後、熊工で所用を済ませ、夜の9時過ぎに人吉(学校)に帰って来ました。不在の間にたまっていた書類に目を通した後、HPを開けたら、午後10時12分現在の総アクセス数は、1107369
この数字、何か閃くものがありました。素数?
いや、違います。素因数分解は次のようになります。
1107369=32×41×3001 ・・・・・・・・・・・①
じゃあ、何かというと、上4桁の数が下3桁の数で割り切れるということです。
即ち
1107÷369=3 ・・・・・・・・・・・・・・・・・②
あまり面白くありませんか?? ちなみに、
上4桁の1107を素因数分解すると、1107=33×41 ・・・③
下3桁の369を素因数分解すると、 369=32×41 ・・・④
となります。
①~④を眺めてみると、何の脈絡もなさそうで何か秘密が隠れていそうで、不思議な気分になり、暫くボ~っと見とれてしまいました。
生徒の皆さんたちは、7桁の数、そして上4桁、下3桁のそれぞれの数の因数にどのような関係があればこのようなことが起こるのか見破りましたか?
心移りしました。いつものように、1107369という数字の並びをそのままにして、加減乗除等の記号を入れて、今日の日付である711を作ってみます。
1×(107×3!+69)=711 → 7月11日(梅雨明け)
これまた、簡単過ぎて面白くありません。もう一ひねり・・・と考えていたら、警備員の方が「まだ残られますか?」と来られました。時計を見たら午後11時。官舎に帰ります。
【校長】
今日は半夏生
いつも本校のHPにお越しいただきありありがとうございます。
また月曜日が始まりました。先週末に期末考査が終わり、月も変わって生徒の皆さんの頭の中は夏休みに向かって一直線といったところでしょうか?
今日は1年の折り返し点にも当たります。日がだんだん短くなっていることを実感している人がどのくらいいるのか分かりませんが、夏至から数えて11日目の今日7月2日は、暦の上で「半夏生(はんげしょう)」と呼ばれています。
朝からラジオで「今日は半夏生」と言っていたのを聞いて、「半夏生」の3文字を初めて目にした時、「はんなつなま?半分夏が生まれる? これっていったい何?」と反応した遠い昔を思い出しました。昔といえば、私、昔、大阪の企業に勤めていて、関西では半夏生の日に行事食としてタコを食べる習慣があったことも思い出したわけですが、この「半夏生」の意味をよく知らなかったので改めて調べてみました。

葉の片面(表面)だけが白くなることから古くはカタシログサ(片白草)とも呼ばれたり、「半化粧」と表記されたりすることもあるそうです。湿地帯を好む絶滅危惧種とありました。私は目にしたことはありませんが、皆さんは見かけたことありますか?
「半夏生」は昔から農作業の大事な節目とされ、田植えを終わらせる目安とされてきただけでなく、この日の天気で収穫を占ってきたそうです。この頃に降る雨は「半夏雨」と呼ばれ、大雨になることが多いとありました。

手始めに素因数分解をしてみたくなりました。
1100000=25×55×11
従って、その約数は、1, 2, 4, 5, 8, 10, 11, 16, 20, 22, 25, 32, 40, 44, 50, 55, 80, 88, 100, 110, 125, 160, 176, 200, 220, 250, 275, 352, 400, 440, 500, 550, 625, 800, 880, 1000, 1100, 1250, 1375, 1760, 2000, 2200, 2500, 2750, 3125, 4000, ・・・(途中省略)・・・, 55000, 68750, 100000, 110000, 137500, 220000, 275000, 550000, 1100000
の72個あることになります。
次にいつものように、1100000という数字の並びをそのままにして、加減乗除等の記号を入れて、今日の日付である72を作ってみます。
(1+1)×{(0!+0!+0!)!}!!!×(0!+0!)=72
【注】 中学生の皆さんへ もう何度かこの記事の中でも説明をしていることにはなりますが、!は「階乗」または「ファクトリアル」と読み、詳しいことは高校の数学で学習します。ここにある3!なら、3×2×1を計算して6になります。このようにn!なら、n×(n-1)×…×3×2×1の自然数の積を計算します。
そして、0!(ゼロの階乗)は1です。これは約束(決め事)ですから、「どうしてそうなるの?」とか考えたらいけません。
”!”が2つ以上つく「多重階乗」については、高校の学習範囲も超えてしまいます。しかし、そんなに難しくはないので、興味ある方は昨年10月22日の記事「祝 総アクセス数800000件達成」をご覧ください。校長室>徒然雑記帖から入ることができます。
ちなみに、6!!!なら3つおきの階乗ですから、6×3で18になります。
最後に・・・、昨日7月1日(日)は、高校就職では求人受付開始日でした。実質、今日から求人票を持参して企業の方が来校されます。
いい印象を持って帰っていただけるように、生徒の皆さんも日常の所作を今一度点検してください。
【校長】
明日から期末テスト
いつも本校のHPにお越しいただきありありがとうございます。
また月曜日が始まりました。梅雨の中休みでしょうか、朝から青空が広がって気持ちがいい一日です。

今日は私たち教職員の完全定時退勤日に合わせて、生徒の皆さんたちも部活動がない日になります。さっさと下校して、ラケットやバットを鉛筆に持ち替えて、しっかり勉強に励んでください。
勉強に疲れたら夜空を見上げてみてみるといいかもしれません。左側がちょっと欠けた大きな月がぽっかりと浮かんでいることでしょう。淡い月の光が目を優しく癒やしてくれるはずです。満月は3日後の6月28日(木)です。
ところで、「最近アクセス数を話材にした記事が最近出ていませんね」と、私自身も気にしていたことについて、何人かの先生方から声をかけていただいています。
今年、4月6日に6桁から7桁へと1桁あがり100万台になりました。100万に達した後は(およそ1週間後に110万になりそうではありますが)、なかなか興味をひく数字が出現しなかったことによるものです。
本日6月25日16時25分現在の総アクセス件数は、1095470 です。正直、食指が動く数字ではありませんが、久々にやってみます。(数字の並びをそのままにして、加減乗除等の記号を入れて、今日の日付である625を作ってみます)
1095-470=625 → 6月25日
あっという間に立式できましたが、全く面白みがありません。もう一ひねりしてみます。
(1+0!)9+5!-4-[√7]―0!=625 → 6月25日
【注】 中学生の皆さんへ !は「階乗」または「ファクトリアル」と読み、詳しいことは高校の数学で学習します。ここにある5!なら、5×4×3×2×1を計算して120になります。このようにn!なら、n×(n-1)×…×3×2×1の自然数の積を計算します。そして、0!(ゼロの階乗)は1です。これは約束(決め事)ですから、「どうしてそうなるの?」とか考えたらいけません。
この式にはもう一つ見慣れない記号([ ])があります。これはガウス記号と呼ばれ、その数を超えない最大の整数を表す記号です。私の記事では初めて登場する数学の記号になりますが、そんなに難しくはありません。例えば[3.14]=3になりますし、[-0.23]=-1となります。
従って、上の式では√7≒2.645・・・ですから、[√7]=2です。
数学の先生に聞いたところ、ガウス記号は教科書に載っていないので、本校では扱ってないそうですが、教科書に載っていなくても『実数xを超えない最大の整数を[x]と表すこととする』という注意書きを問題文に明示したうえで、大学入試には出題されていますので注意が必要です。就職試験でも前述の [-0.23] =? 程度の問題でしたが、出題されていたのを受検報告書で見た覚えがあります。
ちなみにガウスは、19世紀のドイツの超天才数学者・物理学者です。彼の業績は極めて多岐に渡り、数学や電磁気などの物理学で彼の名を冠した定理や法則が多数存在するんだそうです。
話は大きく変わって、朝のテレビで言っていたことになります。本日、6月25日は、1960年(昭和35年)の今日、自動車による交通が発達し、道路における危険の防止と交通の安全と円滑、道路交通による障害の防止を目的とした「道路交通法」が施行された日なんだそうです。
道路交通法と聞いて、私たち教職員がいつも気をつけておかなければならないことは、「第65条第1項 何人も*、酒気を帯びて車両等を運転してはならない」だと強く思っています。
* 法律解説書の注釈には、「何人」というのは、運転免許を受けている人にかかわらず、全ての人が対象で、車両等とは、自動車はもちろん、電車や軽車両等(自転車等)までを含むとありました。
先月、熊本市で自転車に乗って登校していた高校3年生の女子生徒が酒気帯び運転の人が運転するワゴン車にはねられて死亡するという大変痛ましい事故がありました。どんなに気をつけていても飲酒運転のクルマに巻き込まれたらどうしようもなく、この報に接して大きな無力感を感じました。
生徒の皆さんたちも、もうすぐクルマの運転免許証を手にするはずです。お互いに良き交通社会人でありたいものです。
【校長】
サイン・コサイン何になる・・・♪
公開授業週間の今週、2年生の各教室では、数学で三角関数の加法定理をやっています。「ここって苦労する所なんだよな・・・」と、自分自身も三角関数に手を焼いていた高校時代を思い出しました。
自分が数学教師だったら入門程度の三角関数の範囲でどんな問題を出すだろう・・・と、10問作問してみました。
生徒の皆さん、三択式ですからよかったら解いてみてください。
一部おふざけの問題も入ってますので、あくまでも暇つぶしにどうぞ。
でも、1問20秒のペースで解いていって、7問以上正解だったら、「三角関数検定3級」位の力はあるのでは?と思います。
1 三角関数で、sinは日本語で「正弦」といいますが、cosは何という?
①余接 ②正接 ③余弦
2 三角関数の主役、sinさん、cosくん、tanさんのうち、いつも自虐的にひがんでいると思われるのは誰?
①sinさん ②cosくん ③tanさん
3 アンケートで「三角関数が嫌い」と答えた日本の高校生が、その理由として挙げた中でいつも最上位にあるものは?
① 公式が多い。
② 三角関係を思い出して苦しくなるから。
③ sin、cos、tanとの出会いが「超唐突!!」で「何、コイツら?」の思いをずっと引きずってしまったから
4 三角関数のイロハともいえる三角比(三角形、特に直角三角形の辺の比を考える分野)は、いつ頃どこで産声をあげた?
① 紀元前約2000年頃のエジプト
② 紀元前約200年頃のギリシャ
③ 1740年頃のスイス
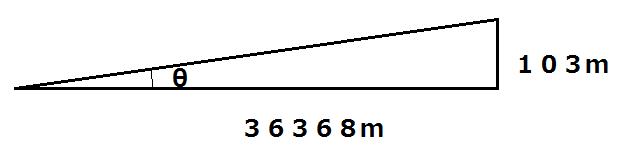
①0.016° ②0.16° ③1.6°
6 次の角度のうち、sinとcosの値が等しくなるのは?
①135° ②225° ③315°
7 sin75° と sin30°+sin45°の大小関係は?
①sin75°>(sin30°+sin45°)
②sin75°=(sin30°+sin45°)
③sin75°<(sin30°+sin45°)
8 中学校で習った「三平方の定理」というのは、【 】定理の特別な場合(θ=90°の場合)だった。
①正弦 ②余弦 ③正接
9 次の勉強嫌いの生徒のほざきに、教師になったつもりで力強く論破してください。一番説得力のあるものは?
「何でcos135°を求める必要があんの?やってる意味ねぇし、人生に三角関数なんか必要ねぇし」
① 三角関数が必要な職業が選べなくなり、人生の選択肢を狭めてしまうよ!
② 私は今その三角関数を君たちに教えることでお金をもらってま~す。
③ 「何の役に立つの?」って疑問は「そもそも何で必要なの?」って疑問なわけで、その答えは「じゃあ、あんた何で生まれたの?」に帰結するよ!
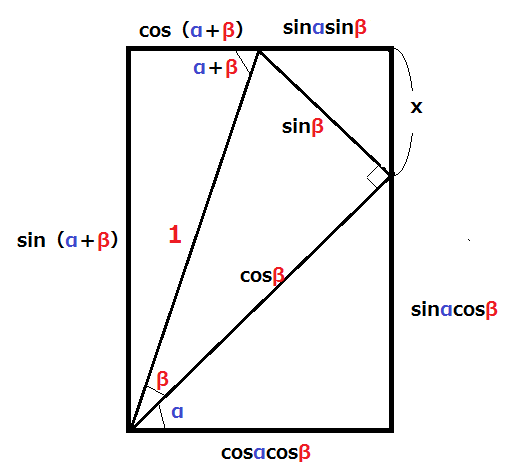
xに相当する長さは?
①cosβsinα
②sinβcosα
③cosαsinβ
【答え】
1:③ 2:③ 3:① 4:① 5:②
6:② 7:③ 8:② 9:①②③(どれを選んでも正解) 10:③
【解説】
1: 数学Ⅰの教科書で確認してください。
既に習ったように、sin(サイン)とcos(コサイン)の間には、sin2θ+cos2θ=1(サインの2乗とコサインの2乗の和は1)という強力な関係があります。その意味で「サインとコサインは一対」であると言っても過言でありません。コサインの英語表記cosineは、co+sineでco-は「~と共に」という意味を作る接頭辞です。なるほど、コサイン(cos)はサイン(sin)と常に共にあるので、この英語表記は分かりやすいです。しかし、日本語になるとcosがなぜ「余弦」と名付けられたのか?
「余」に込められた意味等を追究してみるのも一興かもしれません。
2: 次のサイトを見てみてください。tanさんの嘆きが聞こえてきそうです。
http://nlab.itmedia.co.jp/nl/articles/1710/18/news049.html
数学Ⅰでよく出題される三角関数の式の証明では、tanΘが出てきたらsinΘ/cosΘに直して計算すればうまくいくことが多いです。でも、とかく分数の計算はややっこしくなりがちで、tanΘを見ると「うわ…」と引かれる原因なのかもしれません。
A+B+C=π のとき、tanA+tanB+tanC=tanAtanBtanCなんていう美しい公式もあります。tanさんの良いところを見つけて、エールを送ってください。
3: あるアンケート(自由記述)で②の回答を見たとき笑ってしまいました。
私、三角関数ほど単純なものはなく、三角関係ほど複雑なものはないと思うのですが・・・。
皆さん方が学習してきたように、三角関数はまず直角三角形による定義をしますが、次に単位円による定義に拡張されます。その拡張された定義の元では三角関数は「円関数」と呼ばれることもあります。従って、三角関数からどうしても三角関係を連想される方は、「円関数!!」と5回ほど唱えれば邪念が払われるかもしれません?
4: これは数学史の問題です。その手の本を紐解くと、①の紀元前 2000 年頃、エジプト人がピラミッドの建設で原始的な三角比(1年の最初の頃に習った三角関数)を使っていたとあります。
そして、今2年生の皆さんが習っている三角関数や加法定理は、②の古代ギリシャ時代には確立されていたというので驚きです。
なお、③の1740年ごろというのは、オイラーが次の公式を発見した記念すべき年です。
ei x=cosx+ isinx
実数の世界では全くの無関係のように思われていた指数関数と三角関数が、複素数の世界では親戚どころか兄弟であったことを意味する重要な式です。
この式は、大学の工学部や理学部等に進学すると数学で学びます。今の段階ではこんな式があるんだ・・・という理解で十分です。オイラーはスイス生まれの数学者で、人類史上最も多くの論文を書いた数学者であったと言われています。
5: これは直感で正解してほしいところですが、ある意味難問かもしれません。
実際、人吉から八代方面に向かって国道219号線を車に乗っていると、道がずっとゆるやかな下り坂になっていることに気付くはずです。一体どのくらいの勾配なんでしょう?
これは、逆三角関数と呼ばれる計算をすることで求めることができます。
逆三角関数は数学では習っていないと思いますが、設計などの専門科目で学びますし、計算技術検定2級を受検した人にはおなじみのはずです。
Θ=tan-1(103/36368)を関数電卓に入れると、約0.16と表示されます。
6: 三角関数を単位円で再定義した際に、sinはy座標、cosはx座標になります。従って、第1象限と第3象限でsinとcosが等しくなることがありえます。
ちなみにこの問題は競技クイズ日本一決定戦の予選第1回戦(1問平均10秒のペースで解答する力が要求)に出題されました。
7: 頭の中に単位円を描き、30°、45°、75°それぞれのy座標をイメージしてください。30°のy座標と45°のy座標を重ね合わせた(足し合わせた)高さと75°の高さの比較になります。頭の中に図が丁寧に描ければ答は自ずと③と分かるはずです。
ここでは計算で求めてみます。
sin30°=1/2(=0.5)、sin45°=√2/2です。
ここで√2を約1.4として計算すると右辺は、
sin30°+sin45°=0.5+0.7=1.2
では、左辺のsin75°はいくらでしょう?
既に「加法定理」を学習した皆さんなら簡単です。
sin(α+β)=sinαcosβ+cosαsinβを使って
sin75°=sin(45°+30°)
=sin45°cos30°+cos45°sin30°
=(√2/2)( √3/2)+(√2/2)( 1/2)
=(√6+√2)/4
ここで、先ほどと同様に、√6を約2.4、√2を約1.4として計算すると、
sin75°=(√6 + √2)/4=(2.4+1.4)/4=3.8/4=0.95
従ってsin75°<(sin30°+sin45°)となります。
ここで覚えておいてほしいのは、
sin(α+β)=sinαcosβ+cosαsinβ
であって、
sin(α+β)=sinα+sinβ
にはならないということです。
では、この問題は加法定理を知らないと解けないのでしょうか?
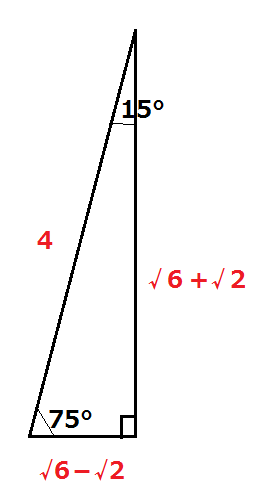
実は、75°と15°の右図のような直角三角形では、辺の比が「 4:√6 + √2:√6 - √2」というのが成り立ちます。
これを覚えておくと15°と75°について、sin、cos、tanの値が図を見ながら、sin75°=(√6 + √2)/4とか、たちどころに分かりますので非常に便利です。
某電力会社の就職試験問題で、sin75°=(□+√2)/4という穴埋め問題で、□に√6を入れさせる問題が出題されたことがあります。加法定理を万一忘れていてもこの辺の比を思い出せば楽勝です。
余談ですが、sinとcosの加法定理そのものの証明が1999年(平成11年)の東京大学の入試で出題されました。「公式は証明してから使うべき」というメッセージなんだろうか、それとも「教科書の内容すら身に付いていないのに難しい問題集を解いている受験生に対する警告」なのだろうかとか色々騒がれました。出来も非常に悪かったそうです。勿論、皆さんは習ったばかりなので証明はバッチリですよね?
8: 余弦定理とは、a2=b2+ c2-2bc・cosAという形の公式です。
今、A=90°のときcos90°=0ですから、a2=b2+ c2となり、これは中学校で習った三平方の定理そのものです。
正弦定理とは、a/sinA = b/sinB = c/sinC という形の公式です。
ちなみに、正接定理と呼ばれているものはありません。
余弦定理を用いることにより、三角形の「2辺の長さとその間の角度」から「残り1辺の長さ」を求められます。また、三角形の「3辺の長さ」が与えられた場合に、すべての角の余弦が求められ、すべての「角の大きさ」を考えることもできます。これに対して、正弦定理は三角形の「1辺の長さ」と「2つの角の大きさ」が与えられた場合に、「残りの2辺の長さ」を求めることができます。慣れるまでどちらの定理を使えばいいのか悩むことがあるかもしれません。
9: これはどれを選んでもマルにします。あなたなら先生からどう言われたいですか?私、自分で解答を作りましたが、3つともとても気にいっています。
この問題の作問のヒントになったのは、「サイン・コサイン何になる・・・♪.」と歌詞の中に出てくる『受験生ブルース』でした。日本のフォークソングの源流を作った男と言われる高石友也の代表曲で、1968年(昭和43年)に大ヒットしました。今でいう「団塊の世代」が大学受験地獄(この言葉は今、死語かも?)を経験していた頃で、当時私は小学3年(9歳)でした。テレビやラジオから毎日のように流れるその哀しい曲を何度も聞いているうちに、サイン・コサインという数学用語がしっかりインプットされました。
高校になって初めてサイン・コサインを習い、「こんなの勉強して何になる?」とその歌詞の意味するところが分かったような気が私自身しましたし、誰でも一度はそう思うのではないかとか考え込んでしまいました。
そういえば、鹿児島県の伊藤祐一郎前知事が2015年(平成27年)8月、「サイン、コサインを女の子に教えて何になる?」などと発言してちょっとした話題になったことがありました。
「いろいろな人生の問題があるため、今の均一な教育の仕組みを変えた方がいい」との思いからの発言だったと釈明されましたが、知事もきっと『受験生ブルース』を聞いて育った世代なのかな・・・と思った次第でした。
私自身も昔、生徒指導部で交通係をしていた頃、多分通学自転車のマナーの悪さに憤慨したドライバーだったんでしょう。苦情の電話の中で「アンタの高校、サイン・コサインとか難しいことを教えなくてもいいから、信号の見方をきちんと指導してくれ!」と罵声を浴びたことがあります。悲しい思い出です。
10: 三角関数はまず直角三角形による定義をします。これはまさにその範囲です。図をよく見ながら丁寧に読み解いていくと必ずわかるはずです。
私は昔からこの図を見るたびに、「本当によく出来た図だな!」と思っていました。あくまでも、α、β、α+βがいずれも鋭角という制限付きではありますが、加法定理がこんなに分かりやすく図の中に表現できるなんて、ある意味凄いです。
是非、sin(α-β)やcos(α-β)が表示できる図も考えてみてください。
【校長】
「ひよどり越え」の名前の由来を探る(その2)
中庭のあじさいの花が二輪咲いています。なぜ紫陽花と書いてアジサイと読むのか知りません。でも、この淡い紫色を見ていると夢見心地の気分にひたれます。
今朝、高校総体の行進の練習がありました。総体が終わるまで梅雨入りは待ってほしいと願っていましたが、とうとう熊本も昨日梅雨入りしてしまいました。
注:以下の記事は、昨年7月20日にアップした「アクセス数682962→鵯(ひよどり)越えの戦い)」の中編になります。(昨年7月20日の記事は→こちら)
本校生が「ひよどり越え」と呼んでいるのは、平家物語の中でも語られる平家滅亡の前兆となる戦い(一ノ谷の戦い)に出てくる呼称です。
いつ頃誰が列車通学生が上ってくるあの坂を「ひよどり越え」と名付けたのか、人吉市史や本校の30周年記念誌などで調べましたが結局分かりませんでした。それどころか意外なことを知りました。それは・・・
「黒坂」
昭和41年4月8日号の人吉新聞に「黒坂の登校階段完成」の見出しに続く次のような趣旨の記述があり、その当時は「黒坂」と呼ばれていたようです。
球磨工業高校通学生徒の一部父兄(主に汽車通学生から市に対し整備を陳情されていた市内城本町の西校登校道路(人吉駅裏の通称黒坂)がこのほどコンクリート階段に整備され、通学生徒をはじめ、地元の利用者は喜んでいる。
同道路は急勾配のため、整備しても一雨降ればすぐ土砂を洗い流し、路面が悪くなり地元民からも整備方が陳情されていた。昨年は悪路を通行する生徒の姿を見て、同町民政委員谷川源昨さんが老身を問わず道路整備に汗を流し生徒から感謝されたこともあったが、今回の整備で通学生も安心して通れると言っている。同道路は延長140m、巾員1mを全長階段にしている。工費は11万6千円。
一方、「大悲坂」とも

そのパンフレットには、「西暦1764年紺屋町の商人達が協力し合い、観蓮寺の観音堂に行く参道を苦労して切り拓き、その事業を後世に残そうと「大悲坂碑」(だいひさかひ)を建てています」とあります。従って、この登り坂は250年前頃は、「大悲坂」と呼ばれていたことになります。

村山観音が安置されているお堂は「大悲殿」と呼ばれているところから来ているのかもしれません。手元の国語辞典によると、「大悲」とは「他人が悲しみ苦しんでいるのをみて助けてあげたいと思う人の心」とあり、どうやら仏教用語のようです。
結局「ひよどり越え」とは?
私、赴任当初から気になっていたことがあります。それは、平家の落人伝説が色濃く残る地域に所在する学校だからある意味当然かもしれませんが、本校も色々と落人伝説と関わりがあるのでは?ということです。どんな点にそれを感じたかと言うと・・・
① 今、話題にしている平家物語にも出てくる「ひよどり越え」のネーミングがまさにそれ。
隣の人吉西小学校の先生方を含め十人近くの行き交う地元の方々に坂道の名前を尋ねてみましたが、その全員が「この坂に名前があるの?」とか「知らない」といった答えばかりでした。人吉西小学校の某先生は、「球磨工生が上がってくる坂」と呼んでいると言われ、「ナルホド!」と思いました。
また、学校評議員をお願いしている1期生の馬場上氏にも尋ねてみたところ、「当時何と呼んでいたか忘れたが、そういう(=ひよどり越え)呼び方はしていなかったはずだ。初めて聞いた」という証言をいただきました。


パンフレットには、「この中の7基の外壁に馬などの動物、武具、文様等の装飾が残っていることから、早くから学界にも注目され、大正10年(1921年)3月3日に国指定史跡となりました。昭和58年から毎年7月第4土曜日には地元城本町住民が中心となって「古墳まつり」が続いています」とありました。
この古墳に沿って、約240人の列車通学生が毎日登下校で使っている365段の階段があり、本校関係者が「ひよどり越え」と名付けているのです。

人吉市に外灯の増設を陳情しても国指定の文化財(大村横穴古墳群)だから形状の変更が難しいらしく、なかなか進んでいないのが現状です。
後編に続きます。
【校長】
Why don’t we go to see a firefly tonight?
いつも本校のHPにお越しいただきありありがとうございます。
朝夕は半袖では少し肌寒いけど、日中は汗ばむ爽やかな初夏の陽気です。そろそろ梅雨入りも気になるところですが、いかがお過ごしでしょうか。
昨日は私たち教師の「完全定時退勤日」ということで、生徒の皆さんは部活がありませんでした。嬉しそうな表情で下校する何人かに「早く帰って何するの?」と水を向けたところ、にこにこしながら異口同音に「勿論、勉強です」と。何かしら可笑しかったです。
私は昨夜8時頃、歩いてコンビニに買い物に行く途中、川べりの草むらに蛍が光を放っているのを目にしました。蛍、今年になって初めてでした。綺麗な清流に恵まれたここ人吉は蛍が舞うんですよね!
昨年、こちらに越してきて、蛍が乱舞する光景を何十年ぶりかに目にして、自然が豊かなんだと改めて驚きました。

そういえば、千年も昔に書かれた「源氏物語」にも、蛍が恋物語にふさわしい感じで描かれています。ズバリ「蛍」と名付けられた巻でです。
手元のシラバスによると、本校の国語では徒然と伊勢は学習しますが、源氏は扱わないみたいですから、生徒の皆さんの中でこのストーリーを知っている方は少ないのかもしれません。ごく大雑把にいうと、玉鬘(たまかずら)という姫君の姿を、ある男性に見せようと考えた光源氏が、暗闇のなかで蛍を放ち、その光に照らし出された姫の美しさに、男性がますます恋心を募らせていくというシチュエーションでした。

暗闇の中のロマンチックな光の明滅に癒されるかもしれません。
【校長】
五月ばかりなどに山里にありく
いつも本校のHPにお越しいただきありありがとうございます。
生徒の皆さん、連休後半をどのように過ごしましたか。
「部活三昧」と聞こえてきそうですが、1日位は休養日があったはずでは・・・?
ということで、私はこどもの日の5日、熊本市の金峰山中腹にある洞窟、霊巌洞*1まで、徒歩で往復(16キロ位)してきました。晩年の5年間を熊本で過ごした宮本武蔵が、この洞窟にこもって兵法書「五輪書(ごりんしょ)」を著したことは、あまりにも有名です。

そんなことを考えていたら、よもぎ餅を久しく口にしていないことを思い出し、どうしても食べたくなって、帰宅後近くのスーパーへ直行。
製菓・パンのコーナーに、最後の1パックが残っていました。某大手パンメーカー製のよもぎ餅大福5個パックで213円。北海道産の粒あん入りです。
そのお味は・・・?
餅の色こそヨモギ色でしたが、その香りはほとんどせず、「こんなものかな・・・」と少し残念でした。夕方のニュースでは温泉施設で「いい香り!」とか言いながら菖蒲湯につかる子どもたちの様子を報じていました。季節の匂いを楽しむ心のゆとりをいつまでも持ちたいものです。
週の初めは大雨です。連休のせいか今週は少し長く感じるかもしれません。高校総体も近づいていますが、あと10日で中間考査。特に、1年生にとっては高校で初めての定期テストになります。ぜひ、計画を立てて学習を始めてください。
*1うっそうと茂る樹木におおわれ、神秘的な霊場として知られる雲巌禅寺(うんがんぜんじ)の裏山に所在します。洞窟内には岩戸観音(いわとかんのん)の名で呼ばれる観音像が安置されています。
*2【口語訳(意訳)】車の車輪に踏まれた蓬が輪が回る時に、ふっと剥がれて車の御簾などに当たり、パシッと微かな音を立てて引っかかるのが趣(おもむき)がある。
【校長】
飛行機雲に想う
いつも本校のHPにお越しいただきありありがとうございます。
月が変わり、いよいよ平成のカウントダウンが始まりました。大型連休狭間の今日5月2日、学校では朝から進学課外の開講式、そして午後はこの春就職して帰省した卒業生を招いて機械科の生徒を対象に進路講話が行われました。
さて、いきなりですが、生徒の皆さんは飛行機に興味がありますか?
私は高校の頃、鉄研(鉄道研究同好会)に所属しており、東京あたりまでの出張なら今でも鉄道を利用するほうで、飛行機は今一つです。でも、お月様を見るのが好きなので、今日はどのあたりにいるんだろうと空を見上げた際に飛行機を見つけることが多々あり、人吉上空を飛ぶ飛行機に興味を持ちました。
多分、上空の気象条件が整った時だと思います。青空の下、一直線にくっきりと力強い雲*1を引く飛行機を目にすることがあり、嫌なことも忘れていつまでも目で追ってしまいます。そうこうしているうちに、人吉上空は、高高度を飛ぶ国際線の旅客機の航路が設定されているのでは?と思うようになりました。
はるか上空を飛ぶ機影を眺めていると、
あれはどこから飛んできてどこに向かっているんだろうとか思いませんか?
私はとても気になります。
知っている人も多いかもしれませんが、リアルタイムで世界中の飛んでいる飛行機が分かるという「Flightradar24」というスマホ用のアプリがあります。今、この瞬間飛んでいる飛行機が、どこを飛んでいて、どんなルートで、高さとスピードはどれぐらいかを地図上に表示してくれるもので、コックピットからの仮想の眺めも見ることができるというものです。(ADS-Bという航空機が現在の位置と高度を絶えず送信するシステムを使っているらしいです)無料版と有料版がありますが、無料版でもインストールしていると結構楽しめるお薦めの神アプリです。
ということで、私、飛行機を見つけると、いつもこのアプリを開いて検索してしまいます。あくまでも私が人吉の空を見上げて確認した飛行機を調べた限りの話になりますが、本市上空を飛ぶ国際線には以下の便がいました。(そのアプリの画像を貼り付けて皆さんにお見せすることができればいいのですが、著作権上その行為が許可されているのかどうか不明ですから、フリーの白地図にいくつかの路線のイメージを書き込んだものを代わりに載せておきます)
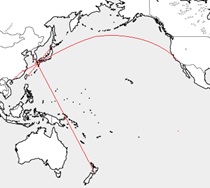
バンコク(タイ)-新千歳、台北-成田、
台北-福岡、マニラ-福岡
仁川(韓国)-グアム、仁川-ウェリントン(ニュージーランド)、
仁川-シドニー(オーストラリア)
上海-サンフランシスコ
重慶(チョンチン:中国)-サンフランシスコ
いかがでしょうか、写真にあったように、人吉上空でいくつかの航路が十字に交わっていることがどういうことかお分かりだと思います。
私は、高校・大学の頃、故城達也さんの素敵な声のナレーションで始まる「ジェットストリーム」*2という深夜ラジオの番組を聴いて育った世代です。だからでしょうか、国際線の飛行機に乗ったことこそ数回しかありませんが、翼のランプを点滅させながら夜間飛行をしている飛行機を眺めると、明日の朝どこに降り立つのだろうかと、この空のもと繋がっている異郷の街や情景を想像してしまい、一緒に乗っていきたくなります。
若葉が美しい季節、今日は八十八夜(立春から88日目)、あと3日で立夏、往く春を惜しむ頃です。生徒の皆さん、有意義な連休後半をお過ごしください。
*1飛行機雲はジェットエンジンからの排気ガスが核になり、水蒸気が凝結して生じるもので、上空の環境によってできる時とできない時があります。どんな時にできるのか調べてみて驚きました。飛行機雲が現れすぐ消えずに長時間残る時は、空気中の水蒸気が多いことを示し、何と、天気が下り坂の前兆なんだそうです。そういうこともつゆ知らず、この歳までポカンと眺めていたとは・・・!?
ちなみに「飛行機雲」は、英語でairplane cloudではなく、contrail [コントレイル]と綴るんだそうです。これは、condensation trailからできた単語でcondensationは「(気体の)凝縮・凝結」、trailは「跡」の意味です。
*2その番組のオープニングナレーションは次のとおりでした。CDまで購入して何度も聴いたので今でも諳んじて言えます。皆さんも声を出して読んでみませんか?これは「声に出して読みたい日本語」だと思います。
遠い地平線が消えて、ふかぶかとした夜の闇に心を休める時、はるか雲海の上を音もなく流れ去る気流は、たゆみない宇宙の営みを告げています。
満天の星をいただく、はてしない光の海をゆたかに流れゆく風に心を開けば、きらめく星座の物語も聞こえてくる、 夜の静寂(しじま)の何と饒舌(じょうぜつ)なことでしょうか。
光と影の境に消えていったはるかな地平線も瞼に浮かんでまいります。
日本航空があなたにお送りする音楽の定期便ジェットストリーム 、皆様の夜間飛行のお供をするパイロットは私、城達也です
【校長】
3乗の展開の公式
いつも本校のHPにお越しいただきありありがとうございます。
今日の2限目、3階の1年生の教室です。建築科や機械科ではモーメントや力の合成など専門の内容が本格的に始まっていました。また、電気科では数学で3乗の展開をやっていました。
3乗の展開とは、(a+b)3=a3+3a2b+3ab2+b3 の公式を使って(2a+3b)3などを求めるものです。
板書されたこの公式が廊下越しに見えて、自分が高校の時の数学の恩師(故人)のことを思い出してとてもノスタルジックな気持ちになりました。
その先生、中学数学で学んだ2乗の展開公式と3乗、(そして発展的に学ぶ)4乗の展開公式の中に出てくる各項の係数を抜き出して板書され「規則性を見つけてごらん」と水を向けられたのです。
どういうことかというと、
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
各項の係数を抜き出すと
121
1331
14641
なかなか見えてこないかもしれませんが、
(a+b)1=a+b
を2乗の展開公式の上段に加えて、係数の並びを少しずらすと
11
121
1331
14641
のように、綺麗な三角形の形に係数が並んでいきます。そして上の段の係数と下の段の係数の間には規則性があります。
この記事をお読みの1年生や中学生の皆さん、もう見抜けましたか?
上の段の左上の数と右上の数の和が下の段にきています!
この三角形は「パスカルの三角形」(Pascal's triangle)と呼ばれています。圧力や応力の単位[Pa]として工業で学ぶ皆さんにとってはおなじみのフランスのパスカル(1623~1662)ですが、彼が最初に気付いたからということでしょうか?名前が残っています。しかし、数学史を紐解くと、実際にはパスカルより何世紀も前の数学者たちも研究していたようです。
従って、14641の下の段の数字の並びは、1 5 10 10 5 1 となりますので、(a+b)5の展開公式は、
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5 となります。
係数の並びは分かるけどa4bとかがどういう仕組みになっているのか、こんがらがっている人がいるかもしれません。
a について見るとa5, a4, a3, a2, a1, a0(a0=1)のように次数が下がり、
b について見るとb0,b1,b2,b3,b4,b5のように次数が上がっています。ここで、aとbの次数を合わせるといつも5次(5乗)になるということは見逃さないで下さい。
まぁ、こういう公式なんて覚えていなくても、気合いで1つずつ展開すれば済む話なんです。でも、覚えていたほうが速く解けるし、計算による脳のエネルギー消費を節約することができるわけです。最後に・・・
Which do you like better, expansion or factorization?
(展開と因数分解、どちらが好きですか?)
私は断然・・・。
【校長】
初志貫徹・有言実行
いつも本校のHPにお越しいただきありありがとうございます。
ここ数日、199名の新入生が入学式の日に提出した「決意作文」を読んでいます。「精一杯」「しっかりと」「挑戦」といった言葉がちりばめられ「やる気」がビンビン伝わってくる作文がある一方、「ご指導よろしくお願い申し上げます」で締めくくられ謙虚さが感じられる作文まで色々あり、とても感銘を受けます。と同時に、私たち教職員もそれに応えるべく頑張らないといけない!という気持ちがいやがうえでも高まります。
この種の作文は就職の際にもよく書かされるもので、その時は意気込むあまり大きなことを書きすぎないのが美徳なのかもしれません。しかし、高校生の決意作文にそれは求めません。作文で綴った本校で頑張りたいという大志(これは今年度の学校テーマです)、その気持ちをいつまでも忘れないでほしいと心から願っているところです。初心忘るべからず*、初志貫徹です!
* 入学式の定番フレーズでもある「初心忘るべからず」、生徒の皆さんもきっと一度は耳にしたことがあるはずです。およそ600年前、能を大成した世阿弥(ぜあみ:多分歴史で習ったはずです)が著わした「花鏡」の中に見える言葉だそうです。
実は、私もこの言葉を引用して、今年度の入学式の式辞を作っていました。でも、長くなりそうでしたのでやめました。今日、改めて調べていたら、世阿弥がいう「初心」とは、「物事を始めたころの新鮮な気持ちや謙虚な気持ち」を指すのではなく「みじめさや未熟さ」を指していると知りました。即ち、「その心を忘れるな」ということは、「あの頃のみじめな状態には戻りたくない」という気持ちを常にもって、芸事に精進しなさいという意味らしいです。そういう隠された意味を知っていると、また違った感じに聞こえます。
では、決意作文で触れられていた本校で「頑張りたいこと」のランキング6位までと、特に印象に残った記述をいくつか紹介します。
頑張りたいこと No1・・・学習 (169名:84.9%)
No2・・・部活 (160名:80.4%)
No3・・・資格取得( 62名:31.1%)
No4・・・生活面 ( 57名:28.6%)【時間を守る等】
No5・・・学校行事( 44名:22.1%)【体育大会等】
No6・・・友達作り( 35名:17.6%)
○ 他人の意見に耳を傾け、相互が納得する意見を見つけ出すこと、そして何かを頼まれた時にその期待に近い結果を残すことに心掛け、人を愛するのはもちろん人から愛される人になりたい。
○ 私には一つの大きな目標があります。それは○○部の仲間と共に全国の舞台で活躍し、日本一になることです。
○ これからこの学校でものづくりを学ぶ中で、誠実の心を大切にしていきたいです。なぜなら、誠実さがなければ良い作品ができないからです。
○ 部活動では運動部のマネージャーになり、選手を支えながら選手と一緒に成長していけるような部活づくりをしたいと考えています。
○ 私の力で○○部を必ず全国大会に出場させます。
○ 僕の好きな諺に、「為せば成る、為さねば成らぬ何事も、成さぬは人の為さぬなりけり」とあります。この言葉の通り、強い意志を持ち、何事にも挑戦し続けていきたいです。
○ 過去の自分を一度捨て、新たに勉学に励み進化した自分を両親に見せたいです。・・・そして、今までお世話になった地域の方々、友達、家族一人一人に恩返しをしたいです。
○ 「努力は人を裏切らない」この言葉を信じ一日一日を大切にしていきたい。
○ 先輩には敬語を正しく使いたい。
○ まだ人吉球磨から甲子園に出場したことがないので、部活での練習に加え、自主トレを人一倍して県代表として甲子園に出場したい。
○ ○○に就職したいという夢を必ず叶えるためにも、高校で取れる資格を全部取るように頑張ります。資格はお金がかかると思うけど、親に感謝して一発で合格できるように頑張ります。
○ 前期試験の面接で言ったとおり、生徒会長になりたいと思っています。
○ 僕が高校で頑張りたいことは全て校訓に当てはまります。剛健誠実、自主自律、好学敬愛の三綱領はとても大事なので、三年間大切に心掛けます。
○ 将来○○関係に進みたい。そこは英語がとても大切なので英語をしっかりとまじめに取り組みたいです。
○ 中学校では給食があってバランスの取れて美味しいご飯を食べてきましたが、もうそんなのはないので、自分でバランスの取れた食事をしていきます。
○ 私が球磨工業高校で頑張りたいことは、つねに「トップ」に立つということです。
○ 最後に僕が挑戦したいことは3年間無遅刻無欠席を達成することです。
有言実行でいきましょう。頑張れ、新入生!
【校長】
spring storm
いつも本校のHPにお越しいただきありがとうございます。
一昨日午後の春の嵐、すごい強風と大雨でしたが、生徒の皆さんはどのように過ごしましたか?
私は窓を叩きつける雨を見ていて、ヘルマン・ヘッセの「春の嵐」を思い出しました。40年前、大学2年の頃に読んだ覚えがあります。確か切ない恋愛ものだったような気がしますが、内容を思い出せません。
あのころ何を考えてその小説を読んだんだろう・・・、そう思うと居ても立ってもいられなくなり近くの本屋さん(ブックオフ)に大雨の中、車を走らせました。あいにく、ありませんでした。
もう1軒行ってみました。またしても空振りでした。諦めて帰る頃は、風雨もだいぶ治まっていました。側溝の蓋には、飛び散った花びらが一杯。桜は2週間前に終わっています。何の花びらでしょう。ハナミズキ?
司書の坂口先生に伺ったところ、「『車輪の下』はあるんだけど・・・」ということでした。残念です。
【校長】
入学式、無事に終わりました。
いつも本校のHPにお越しいただきありがとうございます。
右の写真は、1年生のある教室の黒板に描いてあったメッセージです。「2時間かけて描いた」と担任の先生から伺いました。歓迎する気持ちがすごくこもっています。
改めまして、新入生の皆さん、入学誠におめでとうございます。真新しい制服やスーツに身を包んで臨んだ入学式、いかがでしたか?
実は、入学式が午後3時前に終わり物品販売等があっている中、午後4時45分からは人吉高校敷地内にある凛然寮(人吉球磨地域共同寄宿舎)で入寮式が行われました。私にとっても新入寮生にとっても大変忙しい一日でした。
入寮式も滞りなく終わり自宅に帰り、遅い夕ご飯を食べてホッとしてHPを立ち上げたら、今現在、午後10時32分現在の総アクセス件数は、1005678。
下4桁が5<6<7<8、末広がりでなかなかいい感じの数字です。
数字といえば、今日入学を許可した生徒・学生数は、本科が199名、専攻科が8名の計207名です。
合計の207は、各桁の和が9で3の倍数ですから、3で割り切れます。実際、素因数分解すると32×23となり約数は1,3,9,23,69,207の6個あります。
私としては、200に1不足している199という数字、丁度200じゃないのがとても残念なんですが、199はそれはそれで気になります。
もうお気付きと思いますが、これは素数です。しかも、各桁の数字を入れ替えてできる919,991も素数*ということで「これは一体どういうこと?」と一気にテンションがあがりました。
* 各桁の数字をどのように入れ替えても素数になる数字のことを「完全順列素数」ということを思い出しました。2桁の素数なら11,13,17,37,79の5個で、これを見つけるのは中学数学のレベルです。3桁なら199以外にどのような素数があるのか・・・?
けっこう面倒でしたが、199以外に113と337を見つけることができました。4桁ではどうなるのでしょうか・・・? 気が遠くなります。
ところで、199という素数は、各桁を循環させると991,919となり、そのいずれも素数ですので、「循環素数」でもあります。実は、199よりも2少ない197も197→971→719と各桁を循環させると、いずれも素数になりますので循環素数ですが、これは完全順列素数ではありません。(197,179,719,971は素数ですが、791が7×113、917が7×131と素因数分解されます)
最初に話題にした総アクセス件数の1005678の5,6,7,8の並びにヒントを得てごちゃごちゃやっていたら、またしても面白い性質をみつけました。何と199は、連続する6つの整数の平方の和で表されるということです。
数式で書くと 199=32+42+52+62+72+82
「美しい!」と見とれて、寝るのも忘れてしまいそうです。こうなると、専攻科の入学生の数である8にも何か意味を見出したくなります。
色々考えてみましたが、特に思いつきません。苦し紛れですが、199と8を結び付けるものとして「8n-1」ということ位でしょうか?
199=8×25-1
(あれ!、1不足が出てきました。199は、8n-1型で表される12番目の素数になります)
話は大きく変わりますが、桜が終わりハナミズキが青空に美しく映える頃となりました。右の写真は校長官舎の庭にあるものです。
歌手一青窈(ひとと よう)さんの歌でも有名なハナミズキ、図書館の植物図鑑によると、日本における植栽は、1912年に当時の東京市長だった尾崎行雄がアメリカ合衆国ワシントンD.C.へ桜(ソメイヨシノ)を贈った返礼として1915年に贈られたのが始まりとありました。日本人が桜を愛するように、アメリカではハナミズキが最も愛されるのだそうです。
明日は対面式、明後日は交歓会と、新入生を対象とした行事が続きます。
【校長】
祝 総アクセス数 百万件達成
いつも本校のHPにお越しいただきありありがとうございます。
本日4月5日、午後3時40分現在の総アクセス件数は、1000000。
ついに、6桁から7桁へと1桁あがり、総アクセス数が百万に達しました。
気の早い話ですが、もし現在のペースのアクセス件数(1日当たり平均1200件)がずっと続くと仮定すると、8桁の最小数である1千万になるのは、2048年12月頃です。その頃、今の生徒たちは40歳前です。どのような人生が開けているのでしょうか。考えるだけでワクワクしますし、自分はその頃どうなっているのだろうかと思うとなぜか切なくなります。そしてその間およそ20年6カ月間、7桁の様々な数を目にすることになります。
ところで、百万という数、とてもウキウキします。平方根(√1000000)は1000で、立方根(3√1000000)は100です。また、常用対数(log1000000)は6ですね。とりあえず素因数分解してみます。胸がドキドキ高まります。
26×56ですから、その約数は、1, 2, 4, 5, 8, 10, 16, 20, 25, 32, 40, 50, 64, 80, 100, 125, 160, 200, 250, 320, 400, 500, 625, 800, 1000, 1250, 1600, 2000, 2500, 3125, 4000, 5000, 6250, 8000, 10000, 12500, 15625, 20000, 25000, 31250, 40000, 50000, 62500, 100000, 125000, 200000, 250000, 500000, 1000000の49(=7×7)個です。
このサイトではこれまで達成したHPの総アクセス数を取り上げて様々な角度から考察をしてきましたが、約数の個数が奇数個になったのは初めてです。以前、奇数個の約数の数について、その数学的な説明をこのサイトでしたことがあります。興味がある方は、校長室>徒然雑記帖から入って、昨年1月15日のサイトをご覧ください。「nが平方数⟺ nの約数の個数は奇数」とか書いてあります。
続いて、いつものように数字の並びをそのままにして、加減乗除等の記号を入れて、今日の日付である45を作ってみます。
((1+0!+0!)!)!!-(0!+0!+0!)(0!)=45 → 4月5日
【注】 中学生の皆さんへ !は「階乗」または「ファクトリアル」と読み、詳しいことは高校の数学で学習しますが、例えば6!なら、6×5×4×3×2×1を計算することになります。このようにn!なら、n×(n-1)×…×3×2×1の自然数の積を計算します。”!”が2つ以上つく「多重階乗」については、高校の学習範囲も超えてしまいます。しかし、そんなに難しくはないので、興味ある方は昨年10月22日の記事「祝 総アクセス数800000件達成」をご覧ください。校長室>徒然雑記帳から入ることができます。ちなみに6!!なら2つおきの階乗ですから、6×4×2で48になります。
そして、0!(ゼロの階乗)は1です。これは約束(決め事)ですから、どうしてそうなるの?とか考えたらいけません。
時間をあまりかけることなく立式できたのですが、できれば「!!」のような仰々しい記号を使わず、すっきりした式を作りたかったです。生徒の皆さん、もっとシンプルな式ができたら教えてください。
話は変わりますが、生徒の皆さんは100万と聞いて、どのようなことを思い出しますか。工業で学ぶ人たちですから、SI接頭辞の1000000 倍がM(メガ)、1/1000000 は µ(マイクロ)ということや、百万分率をppm (parts per million) ということはすぐに思い浮かぶかもしれません。
私は随分前に新聞で読んだある記事を思い出しました。私立文系の大学の受験者で数学(センター試験)を選択した学生としなかった学生の「その後の年収」の追跡調査に関するもので、京都大学の先生が調査したものでした。それによると、数学を受験した人の年収が平均100万円位多いという結果で、当時大変驚いてこの記事を何度も読み直しました。
今回、改めて関連記事を探しましてみたらネット上に残っていました。(興味ある方は「数学受験者の年収が100万円位多い」で検索してみてください)
「数学で鍛えた論理能力は社会に出て活躍の場を広げることにつながるので、子どものうちから数学力を身につけさせることに留意すべきである」という趣旨の記事に接し、生徒たちに数学の大切さについて話をした覚えがあります。
ところで、100万円の分の1万円札束を見たことがありますか?私は銀行で見たことがあります。その厚さ、およそ1cmで横向きに立てることができます。
100万円位ならベテランの行員さんの手にかかるとほんの数秒で数えられるみたいです。実際、100万円近いボーナスを、元行員の妻に手渡したところ「パパッと数えられたので味気なかった」というぼやきを友人から聞いたことがあります。
最後に「百万」が入っている背筋がぞくっとするような言葉を一つ。あまりにも有名なので、耳にしたことがある人が多いかもしれませんが・・・・。
喜劇王チャップリンが制作した映画「殺人狂時代」の中に出てくる次の言葉です。
1人殺せば殺人犯だが、100万人殺せば英雄だ。
この映画、私は見たことがありません。第二次世界大戦末期、「最新兵器」の実験台として、広島・長崎へ「原子爆弾」を投下し、30万人以上もの罪のない一般人を殺し、「戦争の早期終結」との大義のもと美化し、戦勝国の気分に酔っていたアメリカを痛烈に皮肉る内容の映画だそうです。そして、この言葉は20世紀の映画史に残る「名台詞(せりふ)」と呼ばれているようです。
来週の月曜日は始業式、そして入学式です。特に、新入生の皆さん、心の準備はできていますか?そして宿題は終わりましたか?
【校長】
「しづごころ」とは?

春風にあおられ、ヒラヒラと舞い散る桜の花びらを見て、百人一首の33番紀友則(きのとものり ?~905)の歌が思い出されました。
ひさかたの 光のどけき 春の日に
静心なく 花の散るらむ
思い出したのはいいのですが、ふと「しづごころ」とはどういう意味だったんだろうと気になり始め、国語便覧やネット等で調べてみました。以下の現代語訳や解説は、「京おかきの小倉山荘」のサイトからの引用です。
◆現代語訳◆
こんなに日の光がのどかに射している春の日に、なぜ桜の花は落ち着かなげに散っているのだろうか。
◆解説◆
【ひさかたの】
日や月などにかかる枕詞(まくらことば)で、ここでは「(日の)光」にかかっています。
【光のどけき】
「日の光が穏やか」という意味です。「のどけし」には、のんびりとしているな、などというほどの意味もあります。
【静心なく】
「静心(しづごころ)」は「落ち着いた心」という意味。「落ち着いた心がなく」とは、散る桜の花を人間のように見立てる擬人法です。
【花の】
花はもちろん桜のこと。
【散るらむ】
「らむ」は目に見えるところでの推量の助動詞で、「どうして~だろう」という意味。どうして、心静めずに桜は散っているのだろうか、というような意味になります。
◆鑑賞◆
柔らかな春の日差しの中を、桜の花びらが散っていく。こんなにのどかな春の一日なのに、花びらはどうしてこんなにあわただしく散っていくのか、静める心はないのか、という歌です。とても日本的で美しい光景。そんな桜の美しさが匂うような歌といえるでしょう。
ということで、「しづごころ」とは「落ち着いた心」という意味でした。落ち着いた心がなくとは、散る桜の花を人間のように見立てる擬人法(この言葉、久々に聞く懐かしい響きです)だったんですね。散りゆく桜への哀愁が感じられ、この季節、必ず思い出す歌ですが、謎が解けてよかったです。
そういえば、私の好きな在原業平(ありわらのなりひら 825~880)も伊勢物語82段の中に、桜をテーマとした次のような歌を残しています。
世の中に 絶えて桜の なかりせば
春の心は のどけからまし
この歌はとても分かりやすいですね。「この世の中に、まったく桜の花というものが無かったならば、春を迎える人の心は、穏やかでいられるだろうに」という意味です。
業平はこの歌をどんな気持ちで詠んだのでしょうか。勿論、本気で「桜なんか無かったらいいのに」と思っているわけではないはずです。
「美しい桜の花よ、どうか散らずに、このままずっと咲いていておくれ」という、はかない花の命を惜しむ思いや桜を賞賛する気持ちを、あえて逆説的に「桜の花がなければ春はのどかなのに」詠んだのだと思います。
伊勢物語を読んだことがある人は、この業平の歌への返歌として、ある人(作者不明)が詠んだ次の歌が収められていることを覚えているかもしれません。
散ればこそ いとど桜は めでたけれ
憂き世になにか 久しかるべき
「桜は散るからこそ素晴らしいのです。うき世に永遠のものなどないのですから」という意味で、これも分かりやすく共感できますよね。
「散るからこそ桜は素晴らしい!」とは実に思い切って言ったものだと思います。潔く散っていく桜を見ていると、この世の万物が絶えず変化し続けていること、そして、形あるものは必ず滅することに思いが至ります。だからこそ、今この瞬間のかけがえのなさが際立つのかもしれません。
どうも、古来、日本人は桜が大好きで、「もうすぐ咲きそうだ。ああ、咲いた。もう散ってしまった!」と、桜に振り回され過ぎているような気がします。日本人のDNAだから仕方ないのかもしれませんが・・・。
隣の事務室から不要な文書をシュレッダーにかける音がずっと響いていて、春の憂鬱(メランコリー)は一層深くなります。今日は、今年度最後の勤務日です。
【校長】
blooming
今年度もあと2週間。いよいよ押し迫ってきました。
雨の週明けになりましたが、天気に恵まれた土日、学校周辺で春を探してみました。
写真は白ですが、紅やピンクの花もあちこちで見受けます。時おり響くウグイスやメジロの囀りにもうっとりしてしまいます。
本校下のあやめ公園の木蓮、一斉に美しい花が咲き誇っていました。上品な甘い香りを漂わせる白色の花が青空によく映え、この時期つい愛着をもって眺めてしまいます。
木蓮の木は恐竜が生きていた1億年前頃には存在していて、日本では平安時代から栽培されていたとか。

きっと命名者を恨んでいるのかも?何と、絶滅危惧種なんだそうです!

そして、河原には、県の鳥、ヒバリが天高く美しい鳴き声で歌っていました。
『うらうらに照れる春日に雲雀(ひばり)上がり心悲しも独りし思へば』とは万葉集の家持の歌です。春の憂愁(メランコリー)というのでしょうか、雲雀の楽しそうな囀りと自分の憂鬱な物思いの対比が妙です。
【校長】
総アクセス数969696 → 100万の前に一息
土の中で冬ごもりしていた虫たちが地面に這い出てくる日とされる24節気の一つ啓蟄(けいちつ)、今年は3月6日だったようです。それから一週間が過ぎ、あの厳しい寒さが嘘のように暖かい毎日が続いています。生徒の皆さん、いかがお過ごしでしょうか。高校入試関係で家庭学習の日が頻繁にあっていましたので、寝ぼけた虫たちのように調子が狂っている人もいるかもしれません?
昨日は合格発表がありました。昨年、一昨年、ドキドキして過ごしたこの時期を思い出してみるのもしみじみとしていいものかもしれません。
さて、969696とは、昨日3月14日8時12分現在の本校のHPの総アクセス件数です。
このような綺麗な数字を見ると、数字の並びをそのままにして、加減乗除等の記号を入れてみたくなり、昨日の日付の314を作ることに挑戦していました。
(969-6)÷√9-6=315 惜しい、もう一歩
96×(9-6)+9+6!!!=315 あれ~
9!÷6!÷9×6-(9+6!!!!)=315 どうしたんだろう?
【注】 中学生の皆さんへ。
”!”は「階乗」または「ファクトリアル」と読みます。例えば6!なら、6×5×4×3×2×1を計算して720になります。”!”が2つ以上つく「多重階乗」については、高校の学習範囲を超えてしまいます。しかし、そんなに難しくはないので、興味ある方は10月22日の記事「祝 総アクセス数800000件達成」をご覧ください。校長室>徒然雑記帳から入ることができます。
ちなみに6!!!は2つ飛ばしの階乗ですから6×3で18です。また、6!!!!は3つ飛ばしの階乗ですから6×2で12になります。
ということで、お昼ご飯を食べながら20分ほど格闘しましたが、どうしても式を完成させることができませんでした。持ち帰って今度は晩酌をしながら楽しみました。でも、近い数字にはなりますが314はとうとうできず、give upしました。この記事をアップし始めてから初めてで残念です。もし、生徒の皆さんで314になる式を作れた人がいたら教えてください。
ところで、969696というのは、間もなく到達するであろう1000000(100万)の前に敢えて取り上げて、その数字の性質を考察しておくべき数字だと思います。
そこで、その面白さを実感するクイズを作問してみました。問題はわずか3問、○×クイズです。下の「正解と解説」を見る前にちょっとでも考えてもらえれば嬉しいです。
① 969696と紙に書いて180度回転させた後、その数字を裏側から見ると696969になる。
② 696969÷969696と69÷96の計算結果は同じである。
③ 96は1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96の12個の約数があり、69の約数(1, 3, 23, 69)4個のちょうど3倍の約数をもっている。従って、969696の約数の個数も696969の約数の個数の3倍である。
① 正解と解説
× 180度回転させても同じ数字になります。それを裏側から見ると、次のように見えるはずです。→
実際に紙に数字を書いてやってみてください。
それにしても、数字の「6」と「9」、よく似てますよね。昔、担任をしているときに、くじで席替えをしていた際、二つの区別がつくように6には「6」のようにアンダーバーを引いていたのを思い出しました。
十進法のそれぞれの数字がいつ頃発明されたのかよく知りませんが、今改めて疑問に思ったのは、「なぜひっくり返したら同じみたいな記号にしてしまったのか」ということです。0と1から9まで、順番に見ていっても、こんなに似ている記号を使った数字はありません。なぜこういうことになったのか、数学史を紐解くと面白いかもしれません。
② 正解と解説
○ 696969=69×10000+69×100+69
=69×(10000+100+1)
=69×10101
969696=96×10000+96×100+96
=96×(10000+100+1)
=96×10101
従って、696969÷969696=(69×10101)÷(96×10101)
=69÷96
=0.71875
③ 正解と解説
○ 969696を素因数分解すると25×32×7×13×37ですから、その約数の個数を指数に1ずつ足して積を求めると、6×3×2×2×2=144個
一方、696969を素因数分解すると32×7×13×23×37ですから、その約数の個数は3×2×2×2×2=48個
従って、144÷48=3で3倍になります。
しかし、実際にこんな面倒な素因数分解をするまでもなく、②の解説の本質的な意味が分かれば、○になることは自明ですよね!
いかがでしたか?工業高校に学ぶ生徒の皆さん方にとって、数学は大事な科目になります。というより、数字とはこの先、縁が切れないはずですし、まずは近い将来の関門である入社試験で課されるSPIの非言語問題を、快刀乱麻を断つがごとくやっつけていかなければなりません。そんな皆さん方に、数字を見る目や数的処理のセンスが高まるようにとの願いを込めて作問してみました。
最後に、言語系のクイズも2問。
④ 百人一首の69番と96番の両歌で、共通して想起される事物は次のどれか。
ア:花 イ:鳥 ウ:風 エ:月
⑤ 「6」と「9」のように紛らわしい日本語の平仮名を一組挙げよ。
④ 正解と解説
ウ
69番 【能因法師】
嵐吹く 三室(みむろ)の山の もみぢ葉は
龍田(たつた)の川の 錦なりけり
(現代語訳)山風が吹いている三室山(みむろやま)の紅葉(が吹き散らされて)で、竜田川の水面は錦のように絢爛たる美しさだ。
96番 【入道前太政大臣 藤原公経(きんつね)】
花さそふ 嵐の庭の 雪ならで
ふりゆくものは 我が身なりけり
(現代語訳)桜の花を誘って吹き散らす嵐の日の庭は、桜の花びらがまるで雪のように降っているが、実は老いさらばえて古(ふ)りゆくのは、私自身なのだなあ。
生徒の皆さんは、百人一首をどのように覚えていますか?
語呂合わせ(例:うかりける…はげしかれとは → うっかりはげ、なげけとて…かこちがおなる → 嘆け過去)や決まり字で覚えている人がほとんどだと思いますが、詠者や歌番号で覚えている人も数は少ないですがいるはずです。
この問題は歌番号で覚えている人じゃないと難しかったかもしれません。中には、「これやこの ゆくもかえるもわかれてはしるもしらぬもあふさかのせき」→「百首の中で唯一濁点が一個もない歌」のように、特徴を捉えて覚えている人もいるかもしれませんね?
⑤ 正解と解説
平仮名の「さ」と「ち」
左右対称というのでしょうか、改めて見るとよく似ていると思いませんか?
英語のアルファベットの「p」と「q」*もそうですよね。
* pとqで思い出しました。一昨年の京都大学の入試で数学の問題の中で「2つの素数pとqで、pq+qp の計算結果が素数になる組み合わせを全て求めよ」という、ハッと虚を突くような問題が出題(理系・第2問・配点30点)されていました。
式が簡単で美しい対称形ですが難問です。でも、一組なら中学生の皆さんでもすぐに見つけられるはずですし、その一組を答案に書くだけで部分点はもらえるはずです。難しいのは、「全て」というのをどのように証明するかです。
いつか機会があればこのサイトで取り上げるかもしれませんが、果たして何組あるのか、素数が好きな人は知的に格闘してみてください。
今日は、96が3回繰り返された969696をもとに、96と69まで話を発展させました。
実は96は熊本市出身の私にとっては、電話の市外局番096-***-****で何十年もお世話になっているわけで、とても身近な数字だと思っていました。
また、それをひっくり返した69ですが、つい先日来賓として出席した人吉第二中学校の卒業式では、体育館前方に「第69回卒業証書授与式」と看板が下がっていて、「69回目を数えるということは、昭和何年に開校したんだろう?」と指を折りましたので記憶に新しい数字です。
そういえば、2週間前の日曜日、熊本駅の前を歩いていたら、突然署名を求められました。何だろうと説明を聞いていたら「憲法改正に関する『反対』の署名」でした。
日本国憲法で憲法改正について定めた条文は第96条です。そして、自衛隊の役割を明文で書き込むための憲法改正を目指しているのが安倍内閣です。その安倍内閣、今も続く長期政権の源流となる第2次安倍内閣が発足したのが安倍氏を第96代内閣総理大臣として任命された平成24年12月26日でした。この「96」の偶然の一致は何だろうと、つい思ってしまいます。
【校長】
円周率の中の「31415926535」
いつも本校のHPにお越しいただきありがとうございます。今日3月14日は、ホワイトデー?
「俺にはホワイトデーなんてかんけーねーんだよ!」って言っている人もいるかも。そんな硬派の君には「円周率の日」*1がお似合いなのかも?
世の中における円周率の役割を考え、円周率が存在しない世界について思いを巡らそうと、多くの国でこの日を円周率の日と定めているようです。
ところで、円周率については昨年10月2日のこのサイトの脚注でも取り上げたことがありましたが、改めてその定義、大丈夫ですか?
円の直径の長さと円周の長さの比(比率)ですよね。円の大きさ(円の直径)によらず、(円周の長さ)÷(円の直径の長さ)=一定(約3.14) であり、これをπ*2と表します。
とても奥が深い円周率、紀元前から現在まで世界中の人たちが色々な形で研究をしていて、今なお進化し続け、コンピュータを使用した計算では、10兆桁を超えて計算されているようです。手元にある教科書のコラムには、「円周率の値は1961年に10万桁、 1973年に100万桁、 1983年に1000万桁、1987年に1億桁、 1989年に10億桁、1997年に100億桁、1999年に1000億桁、2002年に1兆桁、そしてとうとう2014年に13兆桁まで計算されるに至った」とありました。
このように、無理数(小数点以下で同じ繰り返しをしない数)である円周率、皆さんは小数点以下何桁まで記憶していますか?
義務教育の段階では「3.14」と教わったので、2桁だけの人がほとんどだと思いますが、数学が少しでも好きな人ならば「3.14159」とキリのいい5桁まで覚えている人もいることでしょう。
3.14159265 35897932 38462643383279 5028841971・・・
を「産医師異国に向こう 産後厄なく産婦宮代に虫散々闇に鳴く これに母養育ない」という有名な語呂合わせで覚えている人は40桁まで大丈夫でしょう。
あるサイトには、小学生でも100桁位まで覚えられる語呂合わせが紹介され、どうしてこんなに円周率が人気なんだろう?と不思議ですが、これを覚えるギネス記録もあるようで、何と10万桁を超える記録が認定されているようです。
永遠に続く円周率になぞらえて、3月14日に入籍する人が多い(夫婦のどちらかが数学マニア?)と今朝のラジオで報じていました。そういえば、本校の先生の中にも車のナンバーが「・314」の先生がいらっしゃいます。希望ナンバー制度で取得されたのでしょうか、それとも偶然でしょうか?
このように、延々と割り切れずに小数点以下に数字が続いていく円周率ですが、その小数点以下2,000,000,000(20億)桁までに、任意の数字の羅列があるかどうかを調べるアメリカの研究者のサイトあります。(そのサイト、リンクを張ることが許可されているのか不明ですのでURLの紹介は控えておきます)
Irrational Numbers Search Engine というキーワードを copy paste して検索をかけてみてください。すぐにヒットするはずです。ちなみに、Irrational Numbers(イラショナル ナンバーズ)とは「無理数」のことです。
20億桁までと限りはありますが、任意の数字列を入力すると、それが何桁目に現れるかを検索してもらえるので、結構楽しい暇つぶしができます。
試しに、今日2018年3月14日である「20180314」の8桁の数字の並びがあるかどうか確認してみました。
次のように表示され、小数点以下第2143万2395桁目*3にあることが分かります。検索に要した時間はわずか0.1575秒です。
The numeric string 20180314 appears at the 21,432,395th decimal digit of Pi.
12528181760351422658201803148862764626677917154
^ <-- 21,432,395th digit
Search time was 0.1575 seconds.
「これは面白い!」と、自分の誕生日や気になる数字を次々に調べてみました。色々試した限り、8桁までは任意の数字の並びが全て存在するようです。ワクワクしてきました。
そこで、20億桁までに円周率の数字の最初の並びである「31415926535・・・」がどこまで存在するのか調べてみました。以下、○:「存在した」、×:「存在しない」の意味です。参考までに検索時間も示しました。
8桁(31415926)→○(5036万6472桁目:0.39秒)
9桁(314159265)→○(16億6004万2751桁目:12.78秒)
10桁(3141592653)→×(15.75秒)
11桁(31415926535)→×(20.28秒)
ということで、円周率の数字の最初の並びは9桁まで存在するようです。
ちなみに、「123456789」という9桁の数字の列があるかどうか試したところ、次のように表示され、小数点以下第5億2355万1502桁目に最初の並びがあることが分かりました。
The numeric string 123456789 appears at the 523,551,502nd decimal digit of Pi.
7260489917323889207212345678922486448188070486
^ <-- 523,551,502nd digit
Search time was 4.0000 seconds.
ドキドキしながら、2進数っぽい数字などヘンな数を色々と試してみました。
000000000 →(0が9連続)×
00000000 →(0が8連続)○:1億7233万850桁目
010101010 →(0,1が9つ交互)×
01010101 →(0,1が8つ交互)○:1621万470桁目
111110000 →(十進数では496)○:692万6655桁目
123454321 →(回文数9桁)○:17億7448万3,587桁目
先ほども書いたように、任意の数字の並びが8桁までなら存在するようですが、9桁になると存在しないケースもあるようです。
このプログラムでは制限が20億桁ですが、もっと桁数が広がり、現在分かっているという10兆桁当たりまで検索できるようになれば、10桁、11桁・・・と、任意の数字の並びが存在する可能性も広がるような気がします。
最後に・・・、私が愛用しているマグカップは、周囲に円周率が小数点以下1545桁目まで印刷され、「π」の文字がデザイン的に浮き上がっている優れものです。今日3月14日の「314」があるかどうか、検索ソフトに頼ることなくコーヒーを飲みながら目を凝らして探してみましたが、見つけることができませんでした。そこで検索ソフトにかけてみたら、最初に現れるのは「2120桁目」でした。惜しかったです。
【校長】
*1 今日3月14日は、日本パイ協会が円周率のπにちなんで「パイの日」、日本数学検定協会はこの日を「数学の日」と定めています。
円周率で思い出しました。「アメリカの人口は円周率」という新聞の見出しを見たことをです。今、改めて検索したところ、平成24年(2012年)8月14日のことでした。このことを報じた記事には、「アメリカの人口が、3億1415万9265人になりました」とあり、アメリカ国勢調査局が有頂天になって喜んでいるとありました。「なるほど!これでアメリカの人口は忘れない」と当時、嬉しくなったことを覚えています。
なお、今日はE=mc2の方程式で有名なアインシュタインの誕生日でもあるそうです。
*2 ギリシャ語で周を表す περιμετρoζ の頭文字らしいです。アルファベットに置き換えると、periphereia になるそうで、英語読みなら「ペリフェレィア」に近いのでしょうが、ギリシャ語ではどう発音するのでしょうか?興味津々です。
なお、昨年10月2日のサイト(校長室より>徒然雑記帖 から入ることができます)で、「円周率が3.05より大きいことを証明せよ」という東京大学の平成15年度の理系の入試問題を話題にしました。その際に、「余弦定理(本校では1年生の終わりに数学Ⅰで学習します)を習っていないと難しいので、中学生には無理かもしれません?」とか書いていましたが、何と、中学校で学習する数学の範囲で証明をしている動画を最近YouTubeで見て、なるほどそういう解法があるのか・・・と大変驚きました。
*3 このサイトには、次に表れる桁数も表示してくれる機能があり、次は1億3503万8451桁目、その次は1億3592万5787桁目、さらにその次は2億1034万6676桁目と20億桁までに19回表れることが分かります。平均して1億桁に1回出現といったところでしょうか。
また、このサイトでは、e(ネイピア数)、√2(2の平方根)、Φ(黄金率ファイ)と、他の数学的に永遠と小数点以下が続いていく数字からも、任意の数字の羅列が、何桁目にあるかどうかを検索することができます。
心に残る◯◯◯でした!
無事に○○○が終わりました。最後のHRも終わり、何人かの生徒が挨拶や写真に一緒に収まってほしいと校長室に来るなど、玄関前の喧噪は1時間以上も続きました。
それもやっと収まり、ホッとしてHPを開いたら午後1時47分現在の総アクセス数は、958116でした。
数字の並びをそのままにして、加減乗除等の記号を入れてみたくなりました。
9×5-8-1+1-6=31 → 今日3月1日は○○○
√9×58+1+1+6=182 → ○○○で182人が巣立ちました。
モチロン、○○○に入る3文字は「卒業式」です。
卒業式については、その様子を報じるブログがアップされているようですので、式後の最後のHRの様子を報告します。
各クラスで担任から生徒へ卒業証書が手渡され、生徒一人一人、高校生活の思い出や決意等を語っていました。子どもからの感謝の言葉で涙ぐむ親や、3年間の友達とのエピソードで笑いが湧き起こるクラスもありました。
全クラスとも、とても和やかな最後のHRでした。



来週早々アルバイトの形で職場に入るために、明日上京する人もいるなど、一旦卒業するとみな様々な事情を抱えてきます。明日また集まろうと集合をかけても誰かが欠けるものです。その意味で今日がクラス全員揃える最後の日でした。今日という日を目一杯楽しんでください。
最後にこのことも。式終了後、野球、バレーボール、空手、陸上(投擲)の生徒たちが直ちに後片付けをしてくれました。ありがとうございました。
【校長】
梅と月がいい感じです
今日は午後、ハローワークのコーディネートのもと、地元企業5社をお招きし、「親と子が地域と産業を学ぶ企業説明会」を開催します。本校としては初めての企画になりますが、あいにく高体連70周年記念式典と重なってしまい、学校の責任者として様子を見届けることができないのがとても残念です。
生徒たちの目が地元企業に向くきっかけになればと願っているところです。
さて、昨日2月22日はニャンニャンニャンということで「ネコの日」だったらしく、動物愛護団体が様々なイベントを行ったとニュースで報じていました。それを聞きながら、111、222とぞろ目になるのは1月11日と2月22日だけであり、333以降は存在しないわけで、ネコにこじつけるのも面白いと思いましたが、222という数字にもっと関心を持たないといけないと思ったところでした。
222を題材にした数学の問題を検索してみたら・・・、ありました!
東京にある某ミッション系私立中学校の平成4年の入試問題に「222の約数は【 】である。」という穴埋め問題が出題されていました。
勿論、222を素因数分解すると、222=2×3×37 ですから、
答えは1,2,3,6,37,74,111,222 になります。
小学生を対象とした中学入試ではちょっと難しいのかな・・・と思いました。
話は変わりますが、三寒四温を繰り返して春に向かっていることを実感します。今日はとりわけ日中の日差しが温かく感じます。今朝、通勤途中の道沿いのあるお宅の庭の梅が3分咲きで、思わず写真に収めました。梅の間にうっすら白く見える月はとても趣があるわけですが、梅と月というと、私は条件反射のように平安時代の歌人在原業平(ありわらのなりひら)の和歌を思い出します。
月やあらぬ 春や昔の 春ならぬ
わが身ひとつは 元の身にして
というものです。あの月は昔と変わったのだろうか。この梅の咲く春の景色は昔と変わっているのだろうか。いや、どちらもあなたと一緒に見上げた美しい月であるし、かぐわしい香りを楽しんだ梅の花である。しかし、あなたがいなくなり一人ぼっちになってしまった今、私の周りのものは何もかも変わってしまった気がする。私だけは元とのままで変わらないのに・・・と、世の無常と手が届かない所に行ってしまった恋人に思いを馳せ嘆いている歌です。何と切ないんでしょう!
今日は上弦の月ですから、日が暮れた頃は南の空高くにあるはずです。今晩眺めてみようと思っています。
【校長】
学年末考査が始まっています
学校は本日から学年末考査が始まりました。廊下に出されたカバンや教科書等が凜とした雰囲気を漂わせています。
試験の様子を巡回していたら、出された荷物の中に可愛い小袋が沢山入った紙袋もあり、多分マネージャーが放課後に部員に渡すチョコかな・・・と思ったところでした。
(「学校にお菓子を持ってきてはいけません」とか、無粋なことを言うつもりはありません)
あるチョコメーカーが主催する「今どきバレンタイン川柳」のサイト、毎年、面白いと思いながら閲覧しています。今年も世相を反映した楽しく笑える川柳が100句紹介されていました。
「俺のチョコ 黙って食う嫁 ちーがーうーだーろー」
というのがあり、一番笑えました。某議員が絶叫していた「ちーがーうーだーろー」っていうのは、今や流行語みたいですね。事務室でこの話題をしたら、「うちの娘も家で言っている・・・」と聞き、少しドキドキしました。また、
「忖度を 学びなさいよ 義理チョコで」
というのも脱帽レベルで面白いと思いました。「忖度」は今年度、本校生が受験した就職試験で、読み仮名をつける問題で出題されていました。国会で口にされなければ、難読漢字のままだったはずなんでしょうが・・・?
話は変わりますが、巡回した時、2年生は「数学Ⅱ」の試験で積分の問題と格闘中でした。その応用である面積を求める問題も出題されていたようです。この様子を見て思い出したことがあります。
先生:毎日1個のリンゴを食べたら、1週間でいくつのリンゴを食べたことになりますか?
生徒:1日1個のリンゴを7日間食べるので、1×7=7で7個です。
先生:このただのかけ算に見える計算ですが、これ実は積分なんです。月曜日から日曜日までの合計をかけ算を使って積分したんです・・・
と、分かりやすく積分の本質を教えてくださった高校の時の数学の先生や、「インテグラルよ永遠なれ」がペンネームだった友達のことです。
あれから40年が経ちました。それぞれどうしてらっしゃるかな・・・と。
話は変わりますが、2月10日から12日の3連休の期間中、県のサーバーの調子が悪かったようでHPへのアクセスがなかなかできませんでした。
多分10日(土)の午前中頃だったはずだと予想していますが、アクセス数が「941149」という数字を通り越しています。
これ、左から読んでも右から読んでも同じという回文数であることに加えて、1も4も9も平方数(12=1、22=4、32=9)であり、「平方数の回文数」であるということも興味深い数字だな・・・と思っていました。
平方数で思い出しました。1~10をそのままの並びで加減乗除等の記号を入れて今年の西暦2018を作ることに格闘したことがあります。その際に、立方数(3乗)を最初に持ってきていたことです。
123+4×5×6+78+91+0!=2018
中学生の皆さんへ
もう何度も書いていますが、式の中にある"!"は「階乗」または「ファクトリアル」と読み、詳しいことは高校の数学で学習します。もし6!なら、6×5×4×3×2×1を計算して120になります。このようにn!なら、n×(n-1)×…×3×2×1の自然数の積を計算します。
式の最後にある0!ですが、0!=1です。これは定義(決め事)ですから「どうしてそうなるの?」なんて考えたらいけません。
【校長】
ビリビリときて思い出したこと
今朝、出勤するとき、山頂に雪をかぶった白髪岳*1の7合目付近の山際から眩いばかりに輝く朝陽が上がり、南の空には下弦の月(有明の月)が寒々と残っていて、とても風情がありました。ところが、学校に着いて鍵穴にキーを差し込んだ瞬間、ビリビリと不快な思いをして、いっぺんに現実に引き戻されました。
そんな嫌な静電気に関して、十日ほど前の人吉新聞の「お天気歳時記」の欄に「静電気が発生する条件は、気温15度以下、湿度20%以下といわれている。嫌な静電気を防ぐには、加湿器などで湿度を上げるほか、・・・」とあり、「ガソリンスタンドでは冬でも水をまいて静電気を予防している」と結んでありました。
ガソリンスタンドと言えば・・・、機械科の1年生の多くが12月に受検した危険物乙種第4類の結果の通知があり、合格率が芳しいものではなかったと報告を受けたことを思い出しました。自ら高い意識をもって学習する姿勢がまだまだ身についていないのかもしれません。次回は今回の反省を踏まえて、計画をしっかり立てて粘り強く勉強してほしいと願っています。
ところで、私自身は高校教師になって機械科で生徒に指導するようになってから危険物の資格を取りました。その勉強をとおして、ガソリンスタンドの店員さんがホースで水をまいている理由は、「静電気対策」*2と知りました。
しかし、それ以前は、「タイヤが水を巻き上げて車体を汚すので嫌だな・・・」と思いつつも都市伝説のように囁かれていた、「同じ入れるなら昼よりも気温が低い朝入れたほうがお得」というドライバー側の立場に配慮して、水をまいて気化熱でコンクリート面の温度を下げることで少しでもガソリンの温度を下げてくれているものとばかり信じていました。
生徒の皆さんはそれがどういうことか分かりますか?
ヒントはガソリンの温度による「体積膨張」です。
物体は温度が上がると膨らんで体積が膨張します。ガソリンの体積は、1℃上昇すると0.00135倍膨張します。この数字を「体膨張率」と呼び、物質によって固有の値をとります。
この値を使うと、例えば冬10℃の気温で50リッターのガソリンが、夏30℃の気温で何リッターになるかが計算できます。具体的には次の公式になります。
体膨張率 × 元の体積 × 温度差 = 増加する体積
代入してみます。
0.00135 × 50リッター ×(30℃-10℃)= 1.35リッター
何と、ペットボトル2本分以上に相当する1.35リッターも膨張し、温度上昇後は51.35リッターになるのです。*3
ご存じのとおり、このところガソリンはリッター当たり140円台前半と、以前に比べ高めの価格で推移していますが、仮に140円とすれば1.35リッター分は140×1.35 =189円相当になります。たいした金額です。
ここでしっかり考えないといけないのは、冬10℃のとき給油するのと夏30℃のときとでは、どちらが189円相当分ドライバーにとってお特なのかということです。
さっそく考えてみましょう。ただし前提として、50リッターが公称のクルマのガソリンタンクは50リッターできっちりで満タンではなく、幾分余裕*4(ここでは51.35リッター分)があるものとします。
また、スタンド地下のガソリンタンク内のガソリンの温度と外気温及び給油ポンプの流量計通過時、並びに車のガソリンタンクからエンジンに入るまでのガソリンの温度は全て同じであるとします。
ドライバー側の立場です。
冬に50リッター入れて夏まで乗らないとすれば、夏には51.35リッターになっているわけですから、ドライバーは1.35リッター(189円相当)得したことになるのでは?
夏まで乗らないというのは、朝温度が低いときに入れて、昼に温度が高くなってから走るということとイメージ的には同じで、ドライバーにとっては給油時の温度が低いほうがいいと思われます。
さて、生徒の皆さん、この考えをどう思いますか?
私は特に問題ないような気がするのですが・・・。
勿論、エンジンに詳しい人は、ガソリンが燃焼するとき、温度が高いときに膨張したガソリンではノッキングが発生しやすくなり、つまり燃焼効率が悪化し、結果的に燃費が悪くなるからプラスマイナスゼロなのでは・・・?とか考え始める人もいるかもしれません。そういう厳密な議論は、今日は保留にしておきます。
ということで、少しでも温度が低いときにガソリンを入れるほうが、「ドライバーにとってお得なのでは?」と思っていたということです。
しかし、実際のところ、スタンドのコンクリート面に水をまくことで地下にあるガソリンタンクの温度が下がるというのは、あまり考えにくいことで、あってもほんの数℃位なのではと思います。ですから、夏でも冬でもまた、朝でも昼でもその温度差の影響を受けることはほとんどないのかもしれません。最近の給油ポンプの流量計には「温度補正機能」がついていると聞いたこともあるので、その場合は温度差のことは完全に無視できるのかもしれません。
実際のところはどうなのかと、ネット上でも色々探してみましたが、現在のところ明確に正解と分かる情報を記載した信頼できるサイトは見つけることができていません。ということで、ここでは「静電気対策」ということで整理したいと思います。
最後に・・・、色々調べている中でガソリン給油機は±0.3%~0.5%程度の誤差があるということが分かりました。1000円分給油して3~5円に相当します。得しているのでしょうか、それとも損しているのでしょうか?
【校長】
*1 この白髪岳(しらがたけ)、冬場に麓の人吉盆地から眺めると山頂が雪に覆われていて白髪のご老人の頭のように見えることから、その名がついたらしいです。標高を調べてみたら、1416.7mで、九州中央山地では一番南にある最高峰の山みたいです(一つ北よりの市房山は1721m)。
地元で愛飲されている米焼酎「白岳」(高橋酒造)の名前の由来について、この白髪岳から「我」をはらぬよう「が(=我)」を取り除き、『白岳(はくたけ)』と呼ぶようにしたと、蔵巡りで球磨焼酎ミュージアム白岳伝承蔵を訪れたときに説明を受けました。
*2 水をまいて湿度を高めると物体表面の水分を通して静電気が逃げ、静電気が蓄積しません。
「静電気は乾燥した季節や場所に発生しやすく蓄積されやすい」「夏季、人体に帯電しにくいのは、汗や湿気を通して静電気が地面等に漏れているからである」と危険物取扱者受検教本に書いてありました。
気温が氷点下40 度でも気化するガソリン、それを日々大量に扱うスタンドは給油口などから気化したガソリンが高濃度で漂っている環境にあり、静電気による火花放電が発生すると、それが着火源となり火災や爆発事故が発生することがあります。実際、つい最近も他県でしたが、女性ドライバーがセルフ式のガソリンスタンドで給油しようと給油キャップを開けた瞬間に給油口から突然発火して、髪が焼け顔に火傷(やけど)を負ったというニュースを耳にしました。
しかし、今思えば、セルフのガソリンスタンドは水まきをしている光景を見たことがないような気がします。それは「静電気除去パッド」を設置し、ドライバー自身にそれに触れる努力義務を負わせているからかな・・・と思ったところです。
*3 ガソリンが凄く膨張することに改めて驚かされます。実際、ガソリンの体膨張率は水の16倍もあります。
*4 ガソリン等を容器に収納するとき、上部に空間容積を必要する理由は、収納されている液体の体膨張による体積の増加で容器が破損するのを防ぐためです。
生徒、よくやってる!
厳しい冷え込みが続いています。
今朝の花壇、8cmほどの高さで立つ霜柱に「こんなに長いのは初めて見た」と感激しました。ところが、校舎の陰にあるからでしょうか、日が傾き夕方4時半を過ぎてもご覧の通りほとんど解けておらず、改めて人吉の寒さを実感しました。
そのような折り、建築科の実習棟からトントントンと聞こえましたので、何を作っているんだろうと寄ってみました。
2月10日に実施される技能検定(建築大工)に向けての練習なんだそうです。

これまた初めて見る迫力ある光景でした。今までものづくりコンテストなどで10人位が一つの部屋で競っているのは何度も見てきましたが、これほど多くの生徒たちが一斉に練習をしているとは・・・。
ノミに向かって一心不乱に槌をふるう光景、校歌に「勤労の槌をふりつつ ふきあぐる汗を誇らん♪」を想起させ、ものづくりに対する真剣な眼差しも相まって圧倒されました。
担当の先生によると、建築科の生徒、専攻科の学生が3級に計27人、2級に計17人が受検するとか。
凍てつく寒さの中ですが、手元が狂ってげんのうで手を打たないように注意して頑張ってください。
【校長】
大〆の授業
私自身、花束贈呈などセレモニー的に行われていた大学教官の「最終講義」は別として、高校の最後の授業はほとんど記憶がありません。しかし、今でもその日の天気まで思い起こせるのが一つだけあります。それは国語の授業です。まだ若い先生でしたが、人生についてしんみりと考えさせられる内容を最後の授業の教材にしてくださいました。伊勢物語の最終段(125段:ついに行く道)です。この中に出てくる
つひに行く 道とはかねて 聞きしかど 昨日今日とは 思わざりしを
を紹介して解説と鑑賞をされたのです。
これは「ちはやふる・・・」の百人一首で有名な在原業平(825~880)が、病気で伏せたときに詠んだ歌とされています。
人は皆死ぬということは誰でも知っているわけですが、それがいよいよ自分の身になっての驚きと嘆きを詠んでいます。人が必ず行かねばならない道(死)なのだとは聞いて知っていたのだが、こんなにも突然その時がこようとは思いもよらなかったなぁ。人の明日はわからないものであり、そうしたことがあると分かっていたなら、また別の生き方もあっただろうに・・・といったところでしょうか。
特に技巧がないので、今を生きる私たちが普通に読んでも分かりやすく、源氏物語の主人公、光源氏のモデルともされる華やかな生涯を送った業平の生涯を考え合わせると、より強いインパクトを感じます。
古典の文法を覚えるのが苦手で、いつの間にかなるべく関わらないようなっていた古典の授業の受け方を「もっと真面目にやっておけばよかった、時既に遅し・・・」と暗澹たる気持ちになり、この時ほど悔いたことはありませんでした。
そんな私も教職に就き、「やはり教師としては、最後の授業や最後の課外というのは、生徒たちにとって後で思い出してもらえるくらい印象的であって欲しいものだ」と常々考えていました。どんな展開になるのだろうかと、いつもより緊張しながら職員室を出ていたことを思い出します。

左の写真は、機械科3年A組の最後の最後、6限目の大〆の授業の様子です。テスト前ということで、自習をしていました。高校最後の定期考査、頑張ってください。
そして、保護者の皆様方にとってはお弁当作り、本日が実質的に最後になりました。生徒たちはいつも以上に味わって食べたはずで、親子共々感慨深いものがあることでしょう。(右の写真は建築科3年のお昼ご飯の様子です)
生徒たちは帰ってから感謝の言葉を口にしたでしょうか?3年間大変お世話になりました。
【校長】
課題研究発表会を見学して
3年生の課題研究の発表会、全科とも少しずつ見学させていただきました。1年間の取組を、わずか10分程度の中で後輩たちにも分かりやすくプレゼン(発表)することはとても難しかったことと思います。課題設定の理由、取組経過、苦労した点、感想を上手に盛り込み堂々と発表している班が思いのほか多いように見受けました。2年生の聴く態度も総じて立派でした。
御指導いただいた先生方には大変お世話になりました。
3年生の皆さん。機械科と電気科では挨拶でも触れたことですが、進学にしても就職にしても今後プレゼンをする機会は多いはずです。中には、会社の命運をかけたプレゼンをすることになる人もきっといることでしょう。今後目にする他人のプレゼンの良い点はどんどん取り入れ、磨きをかけていってほしいと思います。
ところで、どういう文脈だったか覚えていませんが、幸福論を扱ったある本に「日本人は課題を見つけそれを解決するための取組を行うことに、幸せを見いだす民族である・・・」との一文を読み、思わず「そうだよね!」って頷(うなず)いたことがあります。
その一文を念頭において、平成12年度から段階的に始まった学習指導要領で小・中・高校に入ってきた「総合的な学習の時間」(専門高校では「課題研究」で代替)の「ねらい」を改めて読み直してみます。
横断的・総合的な学習や探究的な学習を通して,自ら課題を見付け,自ら学び,自ら考え,主体的に判断し,よりよく問題を解決する資質や能力を育成するとともに,学び方やものの考え方を身に付け,問題の解決や探究活動に主体的,創造的,協同的に取り組む態度を育て,自己の生き方を考えることができるようにする。
何と小・中・高校同一文言です!そして、課題を解決する中で身に付けた能力を、自己の生き方を考える態度の育成に繋ぐことを求めています!!
なるほど、それがうまくいけば、人は(日本人は?)喜びや幸せを感じるんだろうな・・・、と漠然と納得してしまいます。
話は変わりますが、多くの皆さんが就職する製造業の生産現場では、「カイゼン」活動が活発に行われていることをテレビ等で見聞きしている人も多いはずです。いわゆる「改善」のことで、作業効率の向上や安全性の確保などに関して、現場の作業者が中心となって生産ライン等の問題点を見つけ、知恵を出し合いその解決をはかっていくものです。
この概念は海外にも「kaizen」という英単語で広く普及し、とくにトヨタ自動車のカイゼンは有名で高く評価されています。活動内容としては、3年生の皆さん方が1年間取り組んできた課題研究のイメージで捉えてもらっていいのですが、課題研究ではそれほど強く言われなかったかもしれないことが一つだけあります。それは、どれだけのコスト削減に繋がったか、即ち結果を数字で表現するなど定量的であることが求められることです。
私自身昔、ものづくり企業に勤めていたことがあります。当時の資料は退社時に返却していますが、研修時にとったノートにカイゼンの進め方をメモしたものが出てきましたので、改めて読み直してみました。入社を控えている3年生の皆さん方のために参考までに載せておきます。ある意味、普遍的なものであり、課題研究でも同様なプロセスを踏んでいると思いましたので。
問題提起(違和感即ち問題意識を感じる)
↓
問題確認(問題を具体化・定量化し解決すべき問題を明確化する)
↓
目標設定(問題が解決された状態を暫定的に決め、その測定手段を明確化する)
↓
原因分析(問題の原因を特定)
↓
改善策立案(原因を除去する解決策を複数立案)
↓
改善策評価(複数の解決策から1つの解決策を決定)
↓
実行計画作成(解決への段取りを考える)
↓
実行(解決策を段取りに沿って進める)
↓
評価(解決状況を評価し数値化する)
いかがでしょうか、イメージが湧きますか?
脅(おど)すつもりはありませんが、企業に入ったら勤務時間の内外を問わずこの「カイゼン」活動にかなりの時間を割かざるを得ないことが多いにありえます。特にプレゼン(発表会)の前は、遅くまで残って練習をすることもあるはずです。職場の班単位で競う時は、指導役の班長さんがハッスルして若い社員を鍛えます。社長賞とか部長賞とか懸っていることも多く、報奨金まで出るので熱が入るのです。ブ●ックなんて言っていたら務まらないかも?
企業在職中のカイゼン活動の経験があるからでしょうか、課題研究の発表会のシーズンになると、つい次のような思いが頭をよぎってしまいます。
それは・・・、加工貿易(原料や半製品を他国から輸入し、それを加工してできた製品等を輸出する貿易の形態)で立国することが宿命づけられた我が国の産業界(製造業の経営者たち)の要請で、カイゼン活動のための経験値獲得を期待されて、「総合的な学習の時間」などが学校に導入されたのではないかという思いです。深読みし過ぎでしょうか?
【校長】
校長室の新しい絵

それまでの絵は、寒村にポツンと立つ茅葺きの民家を描いたもので、晩秋の侘しい風情も相まって、寂しさが一層募るような風景画(油絵)でした。
今度の絵は、赤い薔薇など色とりどりの花が咲き乱れる中を2匹の蝶が舞うもので、真ん中に置かれた金色の懐中時計との取り合わせが奇抜なB1サイズの水彩画です。
画題は「縛りの中で」。美術部の河野堅君(機械科2年A組:湯前中出身)の作品です。河野君は美術部に所属し、県風景画コンクールで特選になるなどめきめきと力をつけており、将来が楽しみな生徒です。河野君によると、「限られた時間の中で懸命に咲く花の美しさを懐中時計と多くの植物で表現した」ということでした。
花と蝶までは分かりますが、懐中時計がなぜ出てくるのか私には今ひとつ分かりませんでした。スペインの抽象画家サルバドール・ダリが懐中時計をモチーフにした絵を沢山残していることを思い出しながら、「どういう発想でそういうことになったか」と河野君に聞いてみました。しかし、本人も分からないということでした。まさに抽象的で変幻自在なシュルレアリスム(超現実世界)???
「絵を描くことで、心の中が整理できる」と聞いたことがあります。「描く」ということは、心の中に澱(おり)のように溜まった感情を一つ一つかみ砕くように整理し、絵として外に出し、再び自分の中に取り込むという作業に他ならないということでしょうか?鏡に映った自分を見るように、客観的に絵の中の自分の内面を見つめることができるということかもしれません。きっと河野君の心象風景に懐中時計があったのかな・・・と勝手な想像をしました。
私自身は列車など乗り物や工作機械などをスケッチするのは苦になりませんが、絵心はなく、小中高を通して絵が上手な人が羨ましかったです。
だからでしょうか、生徒の入選作を鑑賞するために美術展に足を運ぶことはあっても、日展をはじめ有名な画家の展覧会に足を運ぶことは滅多にありませんでした。
また、天皇の前で二手に分かれて、交互に見事な絵を披露して勝敗を競う絵合(えあわせ)など、そういうバトルが古く平安時代から行われていたことを「知識」として知ったのも40代になって源氏物語を読んでからでした。
さらに、前任校の美術の先生から、「描いている画面に対して集中するので瞑想をしている時のような無我の境地に入ることがある」とか聞いて驚いたこともあります。絵心が欲しかったな・・・と今改めて思います。
色々書き連ねましたが、校長室にしょっちゅう来られるお客さんの中の何人かが「ひょっとして絵が替わりましたか?明るくなりましたね」と気付いてくださいました。私たち人間は、本能的にこういう想像的な芸術の世界を必要とする生き物であるということを実感し、嬉しく思う瞬間です。
【校長】
今年度の就職試験を振り返る
先日のセンター試験では、地理Bで出題された人気キャラクターのムーミンを取り上げた問題*1について、菅官房長官が記者会見で言及するほど波紋を呼んでいます。
私も本校教育の総決算ともいえる就職試験で、どのような問題が出題され、面接で何が問われたのかを知っておくことは大事なことであると思い、3年生の皆さん方が提出してくれた全ての受検報告書に目を通してみました。
社会の出来事を反映した時事問題や面白いお題の作文、唸るような内容のグループワーク、思わず首をひねりたくなるような問題を見つけましたのでご紹介します。(【 】内に地区と業種を示しました。3社以上で出題があった問題は【多数】と表記しています)
1,2年生の皆さん方は、このような問題に近い将来相対しないといけません。特に時事問題は、日頃から新聞を読むなどアンテナを高く張って生活しておく必要があると痛感したところです。今の実力でどのくらい対応できますか?
作文
・あなたは日本昔話の登場人物で誰になりたいか。【中国・電機】
・次の4つの中からあなたが修理できるものを選び、今まで学んだことを活かして修理の手順や必要な道具を詳しく書きなさい。【関東・技術サービス】
①テレビがつかない ②PCでメールが送れない
③自分の家だけ停電 ④充電用掃除機が使えない
・入社3年後の目標を書きなさい。(「20年後の自分について」「どういう社会人になりたいか」等も)【多数】
集団討論
・本校の野球部が全国大会に出場するにあたり、生徒会としてできることは何か。【関東・技術サービス】
・新しく祝日を2日追加するならどの日にどのような名前の祝日を追加するか。また、今ある祝日の中で1日廃止するならどの日を廃止するか。【中部・鉄鋼】
・現代におけるドラえもんの道具を答えよ。【中部・製造】
・無人島へ物を5つ持っていけるとしたら何を持っていくか。【関東・鉄鋼】
・社会人として大切なこと。【九州・電力】
筆記試験(時事問題系の一般常識)
・桐生選手が陸上100mで記録を更新し日本人初の記録を出したが、そのタイムは。【中部・鉄鋼】
・選挙権は満何歳からか。【関東・電力】
・今の内閣総理大臣の名前をフルネームで漢字で書け。【多数】
・平成何年から次の年号に変わるか。【関東・電力】
・隈 研吾氏について何を知っているか。【九州・建設】
・政府や経済界が推奨しているキャンペーンで、毎月末金曜日の夕方に買い物や旅行などに充てることを何というか。【関東・電気】
・最年少プロ棋士の名前は。【関東・電気】
・2016年に国民全員に番号を与える制度が始まったが、その制度の名称は。またそれは何桁か。【多数】
・東京オリンピックがあるのは何年か。【多数】
・今年の甲子園の優勝校はどこか。【関東・建設】
・2017年のアメリカ大統領選で当選し、第45代アメリカ大統領になったのは誰か。【多数】
・今年、人間国宝になった方4人の中から1人の名前を答えよ。【関西・建設】
面接
・ドラえもんとクレヨンしんちゃん、どっちと友達になりたいか。その理由は。
【関東・自動車】
・弊社のHPを見て思ったことは何か。【九州・サービス】
・ジュニア・マイスターとは何か。【多数】
・年代がバラバラの人と一緒に仕事をやっていく自信があるか。その根拠は。(その他「めんどくさいおじさんばかりだけど意見が違ったらどう対処するか」「人との価値観の違いをどう乗り越えるか」等も)【多数】
・運は良いほうか、それとも悪いほうか。【関西・技術サービス】
・英語は話せますか。【関西・建設】
・昨年弊社に入社したあなたの高校の先輩とあなたはどういう関係か。その先輩はあなたの入社をどう考えていると思うか。【中部・鉄鋼】
・原子力発電についてどう考えるか。【九州・電力】
・あなたの学校の教育理念は。【関西・建設】
・人吉はどんな所か。【中国・鉄鋼】
集団工作等
・マシュマロタワーにチャレンジ!!*2【関東・電力】
パスタの乾麺20本、テープ90cm、たこひも90cm、マシュマロ1個(頂上につける) これらを使ってより高いタワーを4人で作りあげる。(説明、個人ワーク、作戦タイム、実際の作業[17分]、反省等を合わせて70分)
・輪投げで高得点を出して勝とう。【中部・鉄鋼】
班で協議後、競技者と応援する人に分かれて実際に対戦競技した後、手順や良かった点や悪かった点を再度話し合う。
その他
・1+2+3+・・・・・・・・+98+99=【 】【多数】
・(5□4)×3□2=1 【多数】
(□に+,-,÷,×を入れて式を完成させる問題を短時間にできるだけ沢山解くもの)
このような算数系の問題は、普段から私のサイトを見て数に関する感覚を磨いておくと得意になるかもしれません。
数学系では前任校の就職試験報告書で思ったことですが・・・、企業によっては次のような三角関数の加法定理を使った計算で導かれることも数学的常識として当然暗記しておくべき事項と捉えているんだと驚いたことがあります。
cos15°=(√□+√2)/4
何とこの問題、本校の受験報告書でも出題の報告があっていました!【関東・電力】
驚いたといえば、国語で「三大和歌集」【中部・電気】を問う問題位なら常識かもしれません。しかし、これも前任校の就職試験報告書の話になりますが、大学の国文科の入試ではないのに、これは一体何?、よほど古典が好きな人事課の社員が作問したの?と思った問題がありました。源氏物語の順序を並べるもので、確か次のような選択問題で出題されていました。
桐壷→帚木→【 】→夕顔→若紫→【 】→紅葉賀→花宴→・・・
ア:葵 イ:末摘花 ウ:空蝉 エ:須磨
全体としては、コミュニケーション能力があるかどうかをみる質問や問題が増えていることをすごく実感しますが、それについてはまたいつか触れます。
【校長】
*1 ノルウェーとフィンランドを舞台にしたアニメーションとして、「ムーミン」と「小さなバイキングビッケ」を挙げ、例示した両国の言語との正しい組み合わせを選ぶ問題です。
この問題について、大阪大学大学院のスウェーデン語研究室は、1月15日に、ムーミン谷がどこにあるかは原作に明示されていないとして「舞台がフィンランドだとは断定できない」という見解を明らかにして、説明を求める意見書を近く大学入試センター試験に提出するとしたと報じられました。
*2 アメリカ発のこのグループワーク、実際に行った様子を特集したあるサイトによると、全体の平均が50cm位の中、最高は92cmだったとか。
別のサイトでは一番高い塔を建てられたのは、建築家のチームだったそうです。本校の建築科が崇城大学主催の爪楊枝タワーコンテストに参加しており、その実績に照らし合わせても、また専門性から考えても当たり前かもしれません。しかし、数多くの大人が参加したこのゲームで、多くの大人より好成績を収めたのが、何と幼稚園の新卒者たちで、一番ひどかったのがビジネススクールの新卒者たちだったとあり、とても意外でした。実際の競技の場面を見てみたいと思いました。盛り上がるんでしょうね?
センター試験に出た約数の個数
「校長室より」のサイトでは、HPの総アクセス数が節目の数を迎えるたびに、その数を素因数分解するなどして、その数に関する話を深めてきました。
例えば1月10日の900000を取り扱った記事では、
900000=25×32×55
従ってその約数は、1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 25, 30, 32, 36,40, 45, 48, 50, 60, 72, 75, 80, 90, 96, 100, 120, 125, 144, 150, 160, 180, 200,225, 240, 250, ・・・(途中略)・・・, 30000, 36000, 37500, 45000,50000, 56250, 60000, 75000, 90000, 100000, 112500, 150000, 180000, 225000,300000, 450000, 900000
の108個です。
と書いていました。しかし、これまでこの記事の中で約数の個数の”求め方”について触れたことはありません。中学校の数学で学習して当然知っているものとばかり思っていましたので。
ですから、1月14日行われた大学入試センター試験の「数学Ⅰ・数学A」の第4問の(1)に次のような問題を見つけて驚いたところです。
144を素因数分解すると
144=2ア×イ ウ
であり、144の正の約数の個数はエオ個である。
慌てて数学の先生に確認したら、「約数の個数については高校の数学Aで学習している」ということでした。私は以前、中学入試で関連問題が出題されているのを見たことがあり、小学生でも知っていることかと誤認識していました。
生徒の皆さんは、「素因数分解して指数を見れば約数の個数が分かる」ということを知っていましたか?公式風にまとめると次のとおりです。
正の整数nが n =p1a 1・p2a 2・・・pkak
と素因数分解できるとき、
nの約数の個数は (a1+1)・(a2+1)・・・(ak+1) 個である。
例えば、12 は22×3と素因数分解できるので、約数の個数は
(2+1)×(1+1)=3×2=6
で6個となります。
センター試験の問題なら、144を素因数分解すると
144=24×32
ですから、約数の個数は、
(4+1)×(2+1)=5×3=15
で15個となります。
従って、正解は、ア:4、イ:3、ウ:2、エオ:15 です。簡単な問題で、ほとんどサービス問題といってもいいかもしれません。
ところが、この問題を通して面白い議論をすることができます。
前回の記事の中で、「過去の記事を引っ張り出し、これまでこのサイトで扱った数について約数の個数を確認しました」とあり、次のように取り上げました。
555555→ 54個(H29.4.3)、 600000→84個(H29.5.20)
666666→ 96個(H29.7.10)、700000→72個(H29.8.2)
777777→ 48個(H29.10.4)、800000→54個(H29.10.22)
888888→128個(H30.1.2)
皆さん、この約数の個数を見て、ある特徴に気付きませんか?
そうです・・・。全部偶数個なんです。
では、約数の個数が奇数になるのはどんなときでしょう。実は・・・
正の整数nについて、
nが平方数⟺ nの約数の個数は奇数
が成立します。「⟺」の記号は、論理学で同値を意味し、「pならばq」と「qならばp」が同時に成り立つとき、pとqは「同値」といい、p⟺qと表します。詳しいことは数学で学習しますので証明等は割愛しますが、「平方数のときに、約数の個数が奇数になる」ことは知っておくべきことだと思います。
センター試験で出題されていた144は122で平方数です。そういえば、平方数である4(22)は、1,2,4の3つ(奇数個)の約数を持っています。
センター試験が終わって、いよいよ二次試験です。現役生にとっては、人生で初めての体験をしているわけで、不安やプレッシャーは大きいことでしょう。どこかの予備校のCMではありませんが、「苦しいときが伸びるとき」これは確かに言えています。本校にもセンター試験を受けた生徒がいます。
「最後の一日まで伸びる」、この言葉を信じて頑張ってください。
【校長】
総アクセス数 900000 → 煩悩を内包する数字?
昨日の始業式、在籍する544人の生徒全員が揃って始業式を執り行うことができればいいな・・・と願いつつ、1週間ほど前から一部の部活動の中で出てきたインフルエンザの広がり具合を心配していました。結局、8人が発熱や体調不良で欠席だったと教務主任から報告を受けました。3学期の第1日目に登校できずに残念だったかもしれませんが、早く平癒するようお祈りします。
さて、900000とは、本日1月10日9時57分現在の本校のHPの総アクセス件数です。
いよいよ90万台に到達しました。現在1日平均1,200件ほどのアクセスをいただいていますので、4月3日前後に予想される100万の大台に乗るまでの3ヶ月ほど「9*****」の数字が続くことになります。
ところで、生徒の皆さん、この90万という数字を見て、何か感じるところはありませんか?私はこういう綺麗な数字を見ると、無性に素因数分解をしてみたくなります。
900000=25×32×55
従ってその約数は、1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 25, 30, 32, 36, 40, 45, 48, 50, 60, 72, 75, 80, 90, 96, 100, 120, 125, 144, 150, 160, 180, 200, 225, 240, 250, ・・・(途中略)・・・, 30000, 36000, 37500, 45000, 50000, 56250, 60000, 75000, 90000, 100000, 112500, 150000, 180000, 225000, 300000, 450000, 900000
の108個です。
それぞれの約数を眺めてみると「当然ありえるよね」という数字ばかりなのですが、約数の個数108に「9」との関連で背筋が寒くなる思いがしました。
「ひょっとして約数108個って初めてじゃない?」と気になり、早速過去の記事を引っ張り出し、これまでこのサイトで扱った数について約数の個数を確認しました。
555555→ 54個(H29.4.3)、 600000→84個(H29.5.20)
666666→ 96個(H29.7.10)、700000→72個(H29.8.2)
777777→ 48個(H29.10.4)、800000→54個(H29.10.22)
888888→128個(H30.1.2)
やはり、初めてでした。
108とは除夜の鐘で衝く回数で、人が持つ煩悩の数*1とされています。
また、数字の9は苦と同音で、死を連想させる4と同様、不吉であるということで漢字文化圏では忌数(いみすう)とされています。各種施設の靴箱の9番は、人気がないのかいつも空いていたり、コインロッカーや病院では4番や4号室が欠番になっていたりするのは、皆さん方も日頃から気付いているはずです。
ということで、「苦に満ちた90万という数字は108個の煩悩を内包する数字では?」というとんでもないことを考えてしまったわけです。
早々、「煩悩」とは何か、なぜ108個あるとされるのか・・・、調べてみました。分かりやすくいうと、「煩悩」とは「嫉妬」や「強欲」みたいなもので、それに囚(とら)われると自分が苦しむことになるということのようです。でも、なぜ108個なのか、仏教の奥義に関係することで今一つ分かりませんでした。凡人は高尚なことに興味を持たないほうがいいということかもしれません。
気を取り直して、いつものように数字の並びをそのままにして、加減乗除等の記号を入れて今日にちなんだ式を作ってみます。本日1月10日は110番の適切な利用を啓発する「110番の日」*2なんだそうです。そのことに思いを致しながら110になる式を作ってみることにします。
9!!!!!!!×(0!+0!+0!)!+0!+0!=110
暫く考えて末、仰々しい式ができあがりました。
【注】 中学生の皆さんへ。”!”は「階乗」または「ファクトリアル」と読みます。例えば5!なら、5×4×3×2×1を計算して120になります。そして、0!=1は定義(決めごと)です。”!”が2つ以上つく「多重階乗」については、高校の学習範囲も超えてしまいます。しかし、そんなに難しくはないので、興味ある方は10月22日の記事「祝 総アクセス数800000件達成」をご覧ください。校長室>徒然雑記帖から入ることができます。
ちなみに9!!!!!!!は6つ飛ばしの階乗ですから、9×2で18になります。
最後に、9を話題にした楽しい計算です。
これは私が中学2年の時に気付いた式です。当時、お年玉で初めてシャープの電卓*3(蛍光管式)を買いました。楽しくて1日中色々な計算をしているうちにこのことに気付きました。
1÷9=0.111・・・
12÷99=0.121212・・・
123÷999=0.123123123・・・
1234÷9999=0.123412341234・・・
12345÷99999=0.123451234512345・・・
123456÷999999=0.123456123456123456・・・
さて、このパターンはどこまで続くでしょう?
ちなみに、123456789÷999999999の次は?
手元の電卓で確かめてください。といっても表示可能桁数の関係で無理かもしれません・・・。9(苦)が一杯で滅入るかもしれませんが、なぜこんなことになるのか秘密に迫ってみるのも一興です。
このような循環小数(repeating decimal)を分数に変換する方法を高校の数学で学んで「なぁ~んだ」と思ったのですが、被除数(割られる数)と同じ桁数の9の連続数で割るとこういう現象が起こることに気付いた時の驚きを今でも懐かしく思い出します。
【校長】
*1 煩悩の内容について、次のような説明を読んだことがあります。
まず、般若心経にも出てくるように、人間には迷いを起こさせる6根と呼ばれる感覚がある。すなわち眼・耳・鼻・舌・身・意。これがそのまま6つの煩悩になる。さらにその6つの煩悩にそれぞれ「好(気持ちがよい)」「悪(不快)」「平(どちらでもない)」の3つの状態がある。6×3=18で、この18の煩悩にさらに「浄(綺麗)」と「不浄(汚い)」という状態が加わる。18×2=36さらに36の煩悩に「過去」「現在」「未来」の3つの時間の状態がある36×3=108これで煩悩108個、ということらしい。分かったような、分からないような??
その他、お釈迦様が説く「四苦八苦」という言葉から、四苦(4×9=36)と八苦(8×9=72)を足して108の煩悩があるという説、1年における月の数(12)と二十四節気(24)と七十二候(72)を足した数という説、色々あるようです。
さらには、そもそも108の数そのものに深い意味はないということでしょうか、次のような説もあるようです。昔から日本では「たくさんの」という意味で8を使っていました。例えば、八百万神(やおろずのかみ)も実際に八百万の神様がいるわけではなく、それくらい無限にいるという意味です。このことから、煩悩の数が108といわれるのも、本当に108個あるわけではなく、たくさんの数という意味で実際、除夜の鐘を200回近く衝くお寺もあるそうです。
ところで、源氏物語は全部で54のストーリーからなることは国語で習ったとおりです。愛執ゆえの嫉妬こそ煩悩の源であることを描き尽くしたこの物語が、108の丁度半分の54帖で終わっていることに何かしら意図的なものを感じます。そういえば、私の持っている数珠(じゅず)は54玉です。
*2 全国の警察で110番の適切な利用を呼びかけるキャンペーンが行われているようです。朝からのテレビで「携帯なくしたから一緒に探して」とか「ファミレスの店員さんが帽子をかぶってなく不潔だから注意して」など、不適切な通報や無言電話などのいたずらが全部で4割近くもあると耳にし、とても驚きました。
*3 当時、こんな楽しいCMがテレビでよく流れていました。
「とかくこの世は計算さ 数と数とのからみあい、足してもダメなら引いてミニかけてもダメなら割ってミニ、こたぁーえいっぱぁつう! カシオミニ♪」
総アクセス数888888 → 元旦早々末広がりのぞろ目
生徒の皆さん、昨日の元旦の日、いかがお過ごしでしたか?
開運を招くお正月の過ごし方は、家で家族などと「ゆっくりと過ごす」ことなんだそうです。また、今では小学校の宿題でしかやらなさそうな「書き初め」も、新年の抱負や目標を墨でしたためることそのものが神様への誓いでもあり、立派な開運行動だとお参りに向かったクルマの中のラジオで聞きました。
私もこたつの中でゆっくり過ごしています。昨日、
何気にスマホで本校のHPをあけてみました。888888とは、昨日1月1日19時17分現在の本校のHPの総アクセス件数です。
元旦早々、末広がりの8のぞろ目*1で何と縁起がいいんだろうと驚いたところでした。
こういう綺麗な数字を見ると、皆さんはどういう心境になりますか?
電子回路に強い人だったら、7セグメントLED(右写真)で8を6つ点灯させる回路図をパッと思い浮かべるかもしれません。
私はというと、数字の並びをそのままにして、加減乗除等の記号を入れてみたくなります。本校が恙(つつが)ない平穏な1年であってほしいという願いを込めて、昨日の日付である11を作ってみることにします。
8×(8-8)+88÷8=11
シンプルな式があっという間にできあがりました。加減乗除全ての演算記号を1回ずつ入っていて何となく気分がいいです。888*2
ところで、888888を素因数分解すると、23×3×7×11×13×37ですから、約数は、1, 2, 3, 4, 6, 7, 8, 11, 12, 13, 14, 21, 22, 24, 26, 28, 33, 37, 39, 42, 44, 52, 56, 66, 74, 77, 78, 84, 88, 91, 104, 111, 132, 143, 148, 154, 156, 168, 182, 222, 231, 259, 264, 273, 286, 296, 308, 312, 364, 407, 429, 444, 462, 481, 518, 546, 572, 616, 728, 777, 814, 858, 888, 924,・・・(途中略)・・・, 31746, 34188, 37037, 40404, 42328, 63492, 68376, 74074, 80808, 111111, 126984, 148148, 222222, 296296, 444444, 888888の128個です。
8のぞろ目の6桁の整数ですから、88や888で割り切れることは一目瞭然ですが、一見割れそうに見えない77や777で割り切れることは素因数分解するまで見破れず、とても意外な感じがしたところでした。
最後に、8のぞろ目を話題にした楽しい計算を2つご紹介します。
まず、これを計算して規則性をみつけてください。
(8×8)+13=
(8×88)+13=
(8×888)+13=
(8×8888)+13=
(8×88888)+13=
(8×888888)+13=
(8×8888888)+13=
さて、このパターンはどこまで続くでしょう?手元の電卓で確かめてください。といっても最大10桁表示でしょうからあと2つしか試し算できないのかもしれませんが・・・。なぜこんなことになるのか秘密に迫ってみるのも一興です。
次の式も超有名で、第172回数学検定準2級でも出題されています。
9×9+7=88
98×9+6=888
987×9+5=8888
9876×9+4=88888
98765×9+3=888888
987654×9+2=8888888
9876543×9+1=88888888
98765432×9+0=888888888
この次に来る数式を書きなさい。
ちなみに準2級は高校1年程度です。数学検定は、本校では受検の実績がないようですが、前任校では数学科が受検希望者に指導をしていました。
1級(大学・一般程度)・準1級(高3程度)・2級(高2程度)のいずれかに合格すると、この検定の問題を作成でき、採用された場合は作成料が作問者に支払われます。全国規模の検定試験の出題者になれるというのは凄い経験だと思います。また、高等学校卒業程度認定試験の必修科目「数学」が免除されますが、これは直接関係ないかもしれません。皆さん、受検してみませんか?
話が横道に逸れましたが、答は勿論大丈夫ですよね。正解は、
987654321×9-1=8888888888 です。
工業高校に学ぶ生徒の皆さん方にとって、数学は将来道具として使いこなしていかない大事な科目です。その意味で数字とはこの先も縁が切れないはずです。そのような皆さん方に、数字を見る目や数的処理のセンスが高まるようにとの願いを込めて、今年もこのサイトを充実していくつもりです。どうぞ宜しくお願いします。
【校長】
*18のぞろ目といえば・・・こんなナンバーのクルマが初詣に行った先の駐車場で、私のクルマの前に駐車していました。桁数が3分の2とはいえ、今日の話題との偶然の一致に一瞬おののきました。
*2888は、ネットの世界でパチパチパチ(拍手)を意味すると聞いたことがあります。自画自賛?
何かしらワクワクする「2018」
明けましておめでとうございます。
今年も本校のHPをどうぞ宜しくお願いします。
皆様には希望に満ちたいい新年をお迎えになっておられることと思います。
私はというと、学校に通う子がいた頃は、元日の朝は(子どもたちの手前)それなりの緊張感があったように記憶しています。でも、みんな巣立ってしまった今、特に大きな感慨もなく8日後に迫った始業式で何を語りかけようかと、こたつの中でとりとめもなく考えています。
とはいうものの、これから1年間お世話になる新年号の2018という数字には何かしらワクワクするものがあります。
2018は、昨年の2017と違い素数*1ではありません。とりあえず素因数分解してみます。偶数ですから2で割れます。
2018 = 2×1009
いきなり、1009という見慣れない数字が出てきました。各位の和は10なので3では割れませんし、暗算すれば7や9でも割れないことに気付きます。素数っぽい香りがプンプンします。しかし、これが素数とすぐに見破ることができる人は少ないと思います。でも実は1009は素数です。ということで、
2018 = 2×1009
でおしまい。従って、約数は1、2、1009、2018の4つしかありません。数学の世界では、4つしか約数がないもの、つまり素因数分解して素数が2個しか出てこない数は、ちょっと特殊な数の仲間に入ります。
調べてみると、一つ前は2005(=5×401)で13年ぶり、一つ後は何と来年2019(=3×673)です。
話は変わりますが、2018は面白い性質を持っていることが、整数論の世界では知られています。それは2つの素数の2乗の和になるということです。分かりやすく表現すると
2018=□2+△2
と書けるということです。是非、□と△に入る数*2を探してみてください。試行錯誤しつつ、ワクワクしながら結構楽しめるはずです。
ちなみに、この一つ前は1970で
1970=112+432 又は 1970=172+412
であり、一つ後は
2042=192+412
となります。従って、2018年は2つの素数の2乗の和であり、このような年は70年間で今年だけ!レアな年という意味で何となくワクワクします。
暇つぶしのついでに、今年の素数日も調べてみました。
素数日とは、2018年1月23日を20180123のように8桁で表すと素数になる日です。ネット上の「素数一覧」のサイトから拾い出した今年の素数日は次の18日ありました。
20180123、20180213、20180221、20180311、20180327、
20180509、20180609、20180621、20180627、20180707、
20180731、20180801、20180807、20181019、20181121、
20181209、20181223、20181229
よく見ると、7月31日と8月1日は連続素数日になっています!
連続素数日の出現頻度について、素数愛好家の研究によると、18世紀から22世紀まで、すなわち1801年から2200年までの400年で52組あるのだそうです。400年間で52組だから、平均すれば7.7年に1回起きる計算になります。それが今年起きるということで、半年以上先のことですが、なんだかワクワクします。
じゃ~あ和暦(平成30年)ではどうなんだ?と、考えるのは自然なことです。30****のような6桁表示の素数日は次のとおりでした。
300109、300119、300221、300301、300317、300319
300323、300331、300413、300427、300511、300623
300719、300721、300809、300821、300823、300929
301013、301027、301123、301127、301211、301219
こちらも全部で24日あります。ただ、2月21日は、何の因縁か西暦、和暦共に素数日です。連続素数日こそありませんでしたが、ますますワクワクしてきました。
ワクワクすると言えば、今年最初の満月が明日1月2日で、2018年中では最も大きく見える「スーパームーン」とニュースで報じていました。
それによると、「月の軌道は楕円で、そのため月と地球の距離が変化する。最も近いときと遠いときの差は最大で約4万8000kmある。月が地球に最も近づくのが近地点で、最も遠ざかるのが遠地点。近地点のタイミングで満月や新月を迎えると『スーパームーン』と呼ばれる」のだとか。
日没の頃、東の空を仰いで、今年初の満月に新年の願いを託してみてはいかがでしょうか。
最後に、本原稿は下の注釈文も合わせて全部で2018文字です。
【校長】
*1 もう何度も素数について取り上げていますが、年の初めですので、その定義をおさらいしておきます。素数とは2、3、5、7、11、13、・・・のように1と自分自身以外では割り切れない数です。
最近、「世界は素数でできている」(角川新書 小島寛之著)という本を読みました。その本の序文にうまい説明があったので引用してご紹介します。
素数とは、「割り切れない」数です。どのくらい割り切れないかというと、1と自分自身以外では割り切れないのです。だから、ある意味では、うとましい数です。例えば、37個のチョコがあるとしましょう。このチョコを同数で分け合うためには、37人で1個ずつ分け合うか、あるいは、1人で全部食べるしかありません。37が素数だからです。まったく融通がききません。チョコの個数が36個であれば、たくさんの柔軟性が生まれます。2人でも3人でも4人でも6人でも、あるいは12人でも18人でも等分に分け合うことができるからです。
*2 答 ○=13、△=43 又は○=43、△=13
今年もあと10日、2017を振り返る2話
3年生のあるクラス、2学期最後の数学の授業でa+biの計算をやっているのが廊下の窓越しに見えました。「想像上の数」を意味するimaginary number の頭文字iをとった虚数*1、まさにこの世に存在しない数です。高校の時にこの数に初めて触れた時のことを思い出しました。
そこで、今日、今年最後の掃除で校長室に来た機械科3年の生徒たちに、虚数についてのイメージや何のために複素数*2を学ぶと思うか尋ねてみました。「実在しない数をなんで勉強するの?」とか「どうせ将来使わないでしょ?」といった回答を期待して、話を深めていきたかったからです。
しかし、うまく真意が伝わらなかったのか、それとも突然ヘンな話題を振られてドギマギしたのか分かりませんが、虚数がこの世に存在しない数だということを理解していた人は確かにいたものの、今ひとつパッとしない感じの回答でした。あまりしつこく聞くと、最近はやりのマスハラ(mathematical harassment :数学の証明を強要するなどして精神的な苦痛を与えること。たぶん)と言われかねませんので、クリスマスの楽しい話題*3に変えました。
前任校で数学の初任者研修会が開催されたことがあります。研究授業後の合評会で、多くの先生方が「数学の良さや楽しさ、数学が日常生活でどのように役立つのかを実感させることを心がけています」と仰っていました。しかし、学力差が激しいとされる数学の実際の授業の中では、「虚数単位『i』は、2乗すると-1になるという独特の計算ルールがあるだけで、それ以外はa,b,cのような普通の文字と同じように計算をすればいいですよ・・・」と指導するのが精一杯で、その数学的意義まで実感できるように指導することは難しいのではないかと思います。
よく、「交流回路の計算で使われる」という話が紹介されますが、具体的に計算式を示すには、まず電気についての説明が必要になります。改めてこの数を高校数学で取り扱うことの難しさを感じたところでした。
私自身は、高校1年の時に初めて虚数に出会いました。どういうストーリーの中でこの数が出てきたのかはっきり覚えていませんが、多分「2次方程式は、解を持つ場合と持たない場合がある。この2次方程式は実数解を持たない。でも、『解なし』じゃ困る。どうしても解がほしい。という中で、無理矢理『2乗すると-1になる数』を考えて解いてみましょう・・・」といった流れで学んだはずです。「何なのそれは?」と反応したかどうかも今では思い出せません。当時は今ほど数字に関する感性はなかったのだと思います。
数学史の本によると、虚数という言葉を初めて書物に書いたのは、「我思う、故に我あり」で有名なデカルト(1596~1650:フランスの哲学者・数学者)とされています。虚数が発見されてから数百年間は「詭弁(きべん)的な数字であり、実用性はない」「ただの想像上の数に過ぎない」と否定的に評価されていたそうです。ですが、オイラーの等式*4で有名なレオンハルト・オイラー(1707~1783:ロシアで活躍したスイス生まれの数学者・物理学者)が虚数のもつ重要性を解き明かした後、その評価は一変したようです。さらに研究が進むにつれ、その存在を仮定して計算に使ってみたら非常に便利であることが分かり、数学者の間で広く使われるようになったとありました。
ということで、数学者の方々にとっては非常に便利な数なんだそうです。でも、虚数が文字通り「虚(むな)しい数」にならないためにも、高校生の皆さん方にどのように有意義なのかということを示さなければならないとやはり思うのです。
そういう思いで、数学は何のために学ぶのかということをテーマにした様々な本に私自身目を通しているわけですが、ある本に次のようなとても興味深い記述があるのを見つけました。
「東に3im進むということは北に3m進むということ? ~ iをかけると90度回転 ~」というタイトルの下、ざっと次のようなことが書いてありました。
私たちは中学校の数学で負の数(マイナス)を導入することにより、「西に3m進む」ことを「東に-3m進む」と表現することができるようになりました。
では、北に進むことを東に進むことを使って表現できないものでしょうか。
今、横軸が実数部分、縦軸が虚数部分を表す「複素平面」と呼ばれる平面を考えてみましょう。その平面上で「4+2i」の表す座標と、「4+2i」にiをかけた (4+2i)×i =-2+4i 即ち「-2+4i」が表す座標を比べてみましょう。
iをかけた後の点Bは、iをかける前の点Aを「原点を中心に反時計回りに90度回転させた」座標にあることがお分かりだと思います。
・・・・・・略・・・・・・
そういうことで、虚数iを導入することにより、「北に3m進む」ことを「東に3im進む」と表現することができるようになります。
このような説明を虚数について初めて学んだ高校1年の時に受けていれば、幽霊みたいなこの数もきちんと居場所ができて、よりとっつきやすく楽しく学べたのではないかと思っています。
前置きが随分長くなりました。それでは本題です。
「2017を振り返る」 第1話
3年生の皆さん、習ったばっかりの複素数の計算です。長い前置きもそのためのものだったわけですが、次の計算をしてみてください。
(44+9i)(44–9i)=【 】
2017になれば正解です。
ちなみに掃除に来ていた生徒たちにもこの計算に挑戦してもらいました。6人全員ができてホッとしました。
2017は素数であり、素因数分解はできませんが、このように複素数の範囲まで拡張すれば「素元分解」ができます。ちなみに、和暦の平成29年も次のように
29=(5+2i)(5–2i)
分解できます。
今年は、西暦も和暦も素数で、6年ぶりのダブル素数ということで、年明け頃、素数ファンは大いに盛り上がっていましたが、「素数は素因数分解できないからつまんない・・・」なんていう声もチラホラ聞こえていました。しかし、4k+1型の素数はこのような形に分解できるのです。
このことについては、5月11日の徒然雑記帳でも既に紹介していますが、あえて複素数の計算を習った直後の皆さん方に、この式を計算してもらい、行く年2017を偲んで欲しいと思い、再び話題にしました。
「2017を振り返る」 第2話
右の年賀状は、今年の初め、日本数学検定協会から前任校に届いていたものです。2017をテーマとした面白い作問です。当時の生徒たちとかなり盛り上った思い出があります。
皆さん、答は分かりますか?
「1つとって」と指示してありますが、それを無視してとりあえず全部の和を計算してみましょう。
13+23+33+43+53+63+73+83+93
=1+8+27+64+125+216+343+512+729
=2025 ・・・①
総和を2017にしたいわけですから、
2025-2017=8=23
よって、とり除くのは23です。
簡単な問題ですが、これは足し算が全部で9項しかないので、このように実際に計算しても手間はたいしてかかりませんが、項数が多くなると大変です。
そこで数列の和を求める公式の登場です。
シラバスによると、本校では数列は習っていないようですが、右のように代表的な3つの公式はそんなに難しい形をしていません。3乗和の公式(上から3つめの公式)を使えば、第9項目までの和ですから、nに9を代入して、①の2025は次のように一発で出ます。
{(1/2)×9×(9+1)}2=452=2025
それでは皆様、Merry Christmas!
【校長】
※1,※2 この記事をお読みの中学生の皆さん方は、「虚数」とか「複素数」は初めて耳にする用語かもしれません。複素数は、皆さんが普段使っている「1」や「3」といった実数と「i」や「5i」といった虚数を組み合わせたもので、「-4+6i」や「5-12i」のように「〇+△i」で表すことができる数を指します。虚数が現実に存在しない数なので、虚数を含んでいる複素数も現実には存在しない数です。
※3 思い出のクリスマスプレゼントを聞きました。朝起きたら、綺麗にラッピングされた算数の問題集が枕元に置いてあったと・・・某君が。驚きました。毒サンタですね。
※4 オイラーの公式とは次の公式です。 ei x=cosx+ isinx
実数の世界では全くの無関係のように思われていた指数関数と三角関数が、複素数の世界では親戚どころか兄弟であったことを意味する重要な式です。大学の工学部や理学部等に進学すると数学で学びます。今の段階ではこんな式があるんだ・・・という理解で十分です。
電気、電波そして物質を構成する電子なども含めて、自然界は波や振動で溢れています。この波や振動現象を調べるためには、三角関数が必要不可欠です。オイラーの公式は、三角関数と指数関数が、虚数・複素数を通じて表裏一体の関係にあることを示しており、この公式を使用すれば、波動・振動現象に関して明確な答えを出すことができます。ちなみに、eはネイピアの数と呼ばれ、e = 2.718281828・・・の値を持ちます。
多くの数学者がこの公式を「人類の至宝」「人類史に残る不朽の名作」となどと表現しています。ちなみに、2004年に第1回本屋大賞を受賞した小川洋子著の小説「博士の愛した数式」(映画化もされました。本校の図書館にあります)の中では、θ=πのときのeiπ = − 1、即ちeiπ +1= 0という形で、博士が数学の中で最も美しい公式として愛していたという設定で登場します。
確かに、解析学・代数学・幾何学という異なる分野において定義された全く起源の異なる3つの数「e, i ,π」が、「1」と「0」という数学の基礎となる数とシンプルな1つの式で結び付けられており、式の意味はよく分からなくてもその美しさに感動します。
総アクセス数 874123 → 電卓のミステリー

1,2年生は、今回のクラスマッチでさらに絆を強めた各学級の力を今後の授業や学校行事に生かし、さらに学年、学校全体の団結力へと高めてほしいと思います。
さて、いくつかの試合を応援後、校長室に戻り、HPを開いたら午前10時58分現在の総アクセス数が874123。
この数字って、何か見覚えがある数字だな・・・!?、何だったかな・・・??と考えていたら、思い出しました。
生徒の皆さんは分かりますか?
ヒントは、電卓で数字を入力するキー(テンキー)です。計算技術検定は勿論、専門の授業でいつもお世話になっている電卓ですが、その配列をさっと頭にイメージできますか?
なぜこの数字に閃くものがあったかというと、テンキーの配列を使って面白い計算があったこと思いだしたからです。
私は教壇に立っていた頃、授業が早く終わって時間を持て余したときなど、電卓を出してごらんとか言いながら、次のように語りかけて計算をさせていました。
電卓のキーは5を中心に8個の数字が正方形の四辺の形状に並んでいます。
これを左右どちら回りでも、どこから始めてもかまいません。
3桁ずつしりとり式に足し算してください。
答えは全部2220です。
例
123+369+987+741=2220
896+632+214+478=2220
412+236+698+874=2220
生徒「わぁ!」
では、辺の角の数(7、1、3、9)を3桁ずつ足し算してみましょう。
結果は2220です。
777+111+333+999=2220
生徒「えええ?」
では、辺の真ん中の数(2、6、8、4)を3桁ずつ足し算してみましょう。
結果はやはり2220です。
222+666+888+444=2220
生徒「何で~?」
じゃあ、対角線の3つの数字を3桁の数として、4つの数を足し算してみてください。どうでしょうか。またもや2220になりました。
159+357+951+753=2220
生徒「すげえ!!」
こういうこともしてみましょう。十字の3つの数字を3桁の数として、4つの数を足し算します。なんとこれも2220です。
258+654+852+456=2220
生徒「わおおお!」
どうやら電卓のテンキーの配列にはミステリーがあるみたいですね。
最後に、次の計算をしてみましょう。今度も始点、時計回り、反時計回りは問いませんので、5を中心にしてまわりの数を3つずつ数えていき、しりとり式で
(3つの数)―(3つの数)+(3つの数)―(3つの数)
という式の中に数を入れてみてください。この計算すると今度は、必ず0になります。
例
874-412+236-698=0
147-789+963-321=0
生徒:「うそおおお!すげえ!!」
今、この記事をお読みの生徒の皆さんはこのミステリーを知っていましたか?ぜひ、電卓を片手に「ぐるっと一回り」・「角」・「辺の真ん中」・「対角線」・「十字」の足し算、そして(3つの数)―(3つの数)+(3つの数)―(3つの数)を実際にして確かめてみてください。
できれば、式を紙に書いてこのミステリーに迫りましょう。これらの証明*は中学生の皆さんでもできるはずです。
【校長】
※ まず全ての足し算が2220になる理由です。紙に書いた計算をもとに、そのミステリーに迫ってみます。
略証
よ~く足し算の内容を見てみましょう。
集約すると
(1+3+7+9)×100+(2+4+6+8)×10+(1+3+7+9)
と
(2+4+6+8)×100+(1+3+7+9)×10+(2+4+6+8)
の2パターンしかないことに気付くはずです。
で、(1+3+7+9)も(2+4+6+8)も「=20」ですから、
結局、
20×100+20×10+20=20(100+10+1)=20×111=2220
となります。
次に(3つの数)―(3つの数)+(3つの数)―(3つの数)が0になる理由です。これも紙に書いた計算をもとに、その謎に迫りましょう。
略証
何でもいいですが、例えば 963-321+147-789 という数で考えてみましょう。
ここで注目するのは、百の位の数、十の位の数、そして一の位の数です。
百の位の数、十の位の数、一の位の数に注目して計算していくと、
900-300+100-700=0
60-20+40-80=0
3-1+7-9=0
となり、それぞれの数を足すとどれも0になります。
では、412-236+698-874という数でもそれぞれの位に注目して確かめます。
400-200+600-800=0
10-30+90-70=0
2-6+8-4=0
となり、やはりどの位の計算も0となります。
つまり、5を中心にして3つずつ数を選んでいき、
(3つの数)-(3つの数)+(3つの数)-(3つの数)
という式の中に入れると、百の位、十の位、一の位ともすべて0となる組み合わせに自動的になるのです。
まだ納得できない!という方もいるかもしれません。では、もっときちんと証明してみます。計算は中学校の数学程度ですから中学生の皆さんもついてこれるはずです。
電卓のどこの数をxにしてもいいですが、例えば2をxと置きます。そうすると、他のキーの数はそれぞれ右の写真に示すように表すことができます。
123-369+987-741を例にやってみます。
x-1を始点に3つずつ数を数えていくと、
{100(x-1)+10x+x+1}-{100(x+1)+10(x+4)+x+7}+
100(x+7)+10(x+6)+x+5-{100(x+5)+10(x+2)+(x-1)}
=100x-100+10x+x+1-100x-100-10x-40-x-7+100x+700+10x+60+x+5-100x-500-10x-20-x+1
=-100+x+1-100-40-x-7+700+60+x+5-500-20-x+1
=-100+1-100-40-7+700+60+5-500-20+1
=-200+700-500
=0
となり、めでたく0になりました!
球磨工の情報を発信中!
リンクはこちらから
学校情報
〒868‐8515
熊本県人吉市城本町800番地
TEL 0966-22-4189
FAX 0966-22-5049
E-mail
kuma-th@pref.kumamoto.lg.jp
熊本県教育情報システム
登録機関
管理責任者 校長 坂本道彦
運用担当者 ホームページ係