2018年6月の記事一覧
明日から期末テスト
いつも本校のHPにお越しいただきありありがとうございます。
また月曜日が始まりました。梅雨の中休みでしょうか、朝から青空が広がって気持ちがいい一日です。

今日は私たち教職員の完全定時退勤日に合わせて、生徒の皆さんたちも部活動がない日になります。さっさと下校して、ラケットやバットを鉛筆に持ち替えて、しっかり勉強に励んでください。
勉強に疲れたら夜空を見上げてみてみるといいかもしれません。左側がちょっと欠けた大きな月がぽっかりと浮かんでいることでしょう。淡い月の光が目を優しく癒やしてくれるはずです。満月は3日後の6月28日(木)です。
ところで、「最近アクセス数を話材にした記事が最近出ていませんね」と、私自身も気にしていたことについて、何人かの先生方から声をかけていただいています。
今年、4月6日に6桁から7桁へと1桁あがり100万台になりました。100万に達した後は(およそ1週間後に110万になりそうではありますが)、なかなか興味をひく数字が出現しなかったことによるものです。
本日6月25日16時25分現在の総アクセス件数は、1095470 です。正直、食指が動く数字ではありませんが、久々にやってみます。(数字の並びをそのままにして、加減乗除等の記号を入れて、今日の日付である625を作ってみます)
1095-470=625 → 6月25日
あっという間に立式できましたが、全く面白みがありません。もう一ひねりしてみます。
(1+0!)9+5!-4-[√7]―0!=625 → 6月25日
【注】 中学生の皆さんへ !は「階乗」または「ファクトリアル」と読み、詳しいことは高校の数学で学習します。ここにある5!なら、5×4×3×2×1を計算して120になります。このようにn!なら、n×(n-1)×…×3×2×1の自然数の積を計算します。そして、0!(ゼロの階乗)は1です。これは約束(決め事)ですから、「どうしてそうなるの?」とか考えたらいけません。
この式にはもう一つ見慣れない記号([ ])があります。これはガウス記号と呼ばれ、その数を超えない最大の整数を表す記号です。私の記事では初めて登場する数学の記号になりますが、そんなに難しくはありません。例えば[3.14]=3になりますし、[-0.23]=-1となります。
従って、上の式では√7≒2.645・・・ですから、[√7]=2です。
数学の先生に聞いたところ、ガウス記号は教科書に載っていないので、本校では扱ってないそうですが、教科書に載っていなくても『実数xを超えない最大の整数を[x]と表すこととする』という注意書きを問題文に明示したうえで、大学入試には出題されていますので注意が必要です。就職試験でも前述の [-0.23] =? 程度の問題でしたが、出題されていたのを受検報告書で見た覚えがあります。
ちなみにガウスは、19世紀のドイツの超天才数学者・物理学者です。彼の業績は極めて多岐に渡り、数学や電磁気などの物理学で彼の名を冠した定理や法則が多数存在するんだそうです。
話は大きく変わって、朝のテレビで言っていたことになります。本日、6月25日は、1960年(昭和35年)の今日、自動車による交通が発達し、道路における危険の防止と交通の安全と円滑、道路交通による障害の防止を目的とした「道路交通法」が施行された日なんだそうです。
道路交通法と聞いて、私たち教職員がいつも気をつけておかなければならないことは、「第65条第1項 何人も*、酒気を帯びて車両等を運転してはならない」だと強く思っています。
* 法律解説書の注釈には、「何人」というのは、運転免許を受けている人にかかわらず、全ての人が対象で、車両等とは、自動車はもちろん、電車や軽車両等(自転車等)までを含むとありました。
先月、熊本市で自転車に乗って登校していた高校3年生の女子生徒が酒気帯び運転の人が運転するワゴン車にはねられて死亡するという大変痛ましい事故がありました。どんなに気をつけていても飲酒運転のクルマに巻き込まれたらどうしようもなく、この報に接して大きな無力感を感じました。
生徒の皆さんたちも、もうすぐクルマの運転免許証を手にするはずです。お互いに良き交通社会人でありたいものです。
【校長】
サイン・コサイン何になる・・・♪
公開授業週間の今週、2年生の各教室では、数学で三角関数の加法定理をやっています。「ここって苦労する所なんだよな・・・」と、自分自身も三角関数に手を焼いていた高校時代を思い出しました。
自分が数学教師だったら入門程度の三角関数の範囲でどんな問題を出すだろう・・・と、10問作問してみました。
生徒の皆さん、三択式ですからよかったら解いてみてください。
一部おふざけの問題も入ってますので、あくまでも暇つぶしにどうぞ。
でも、1問20秒のペースで解いていって、7問以上正解だったら、「三角関数検定3級」位の力はあるのでは?と思います。
1 三角関数で、sinは日本語で「正弦」といいますが、cosは何という?
①余接 ②正接 ③余弦
2 三角関数の主役、sinさん、cosくん、tanさんのうち、いつも自虐的にひがんでいると思われるのは誰?
①sinさん ②cosくん ③tanさん
3 アンケートで「三角関数が嫌い」と答えた日本の高校生が、その理由として挙げた中でいつも最上位にあるものは?
① 公式が多い。
② 三角関係を思い出して苦しくなるから。
③ sin、cos、tanとの出会いが「超唐突!!」で「何、コイツら?」の思いをずっと引きずってしまったから
4 三角関数のイロハともいえる三角比(三角形、特に直角三角形の辺の比を考える分野)は、いつ頃どこで産声をあげた?
① 紀元前約2000年頃のエジプト
② 紀元前約200年頃のギリシャ
③ 1740年頃のスイス
①0.016° ②0.16° ③1.6°
6 次の角度のうち、sinとcosの値が等しくなるのは?
①135° ②225° ③315°
7 sin75° と sin30°+sin45°の大小関係は?
①sin75°>(sin30°+sin45°)
②sin75°=(sin30°+sin45°)
③sin75°<(sin30°+sin45°)
8 中学校で習った「三平方の定理」というのは、【 】定理の特別な場合(θ=90°の場合)だった。
①正弦 ②余弦 ③正接
9 次の勉強嫌いの生徒のほざきに、教師になったつもりで力強く論破してください。一番説得力のあるものは?
「何でcos135°を求める必要があんの?やってる意味ねぇし、人生に三角関数なんか必要ねぇし」
① 三角関数が必要な職業が選べなくなり、人生の選択肢を狭めてしまうよ!
② 私は今その三角関数を君たちに教えることでお金をもらってま~す。
③ 「何の役に立つの?」って疑問は「そもそも何で必要なの?」って疑問なわけで、その答えは「じゃあ、あんた何で生まれたの?」に帰結するよ!
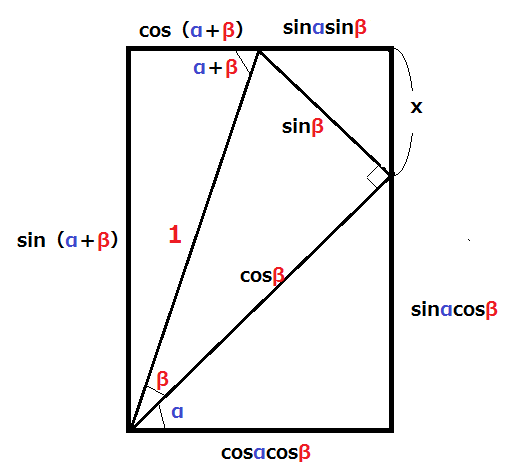
xに相当する長さは?
①cosβsinα
②sinβcosα
③cosαsinβ
【答え】
1:③ 2:③ 3:① 4:① 5:②
6:② 7:③ 8:② 9:①②③(どれを選んでも正解) 10:③
【解説】
1: 数学Ⅰの教科書で確認してください。
既に習ったように、sin(サイン)とcos(コサイン)の間には、sin2θ+cos2θ=1(サインの2乗とコサインの2乗の和は1)という強力な関係があります。その意味で「サインとコサインは一対」であると言っても過言でありません。コサインの英語表記cosineは、co+sineでco-は「~と共に」という意味を作る接頭辞です。なるほど、コサイン(cos)はサイン(sin)と常に共にあるので、この英語表記は分かりやすいです。しかし、日本語になるとcosがなぜ「余弦」と名付けられたのか?
「余」に込められた意味等を追究してみるのも一興かもしれません。
2: 次のサイトを見てみてください。tanさんの嘆きが聞こえてきそうです。
http://nlab.itmedia.co.jp/nl/articles/1710/18/news049.html
数学Ⅰでよく出題される三角関数の式の証明では、tanΘが出てきたらsinΘ/cosΘに直して計算すればうまくいくことが多いです。でも、とかく分数の計算はややっこしくなりがちで、tanΘを見ると「うわ…」と引かれる原因なのかもしれません。
A+B+C=π のとき、tanA+tanB+tanC=tanAtanBtanCなんていう美しい公式もあります。tanさんの良いところを見つけて、エールを送ってください。
3: あるアンケート(自由記述)で②の回答を見たとき笑ってしまいました。
私、三角関数ほど単純なものはなく、三角関係ほど複雑なものはないと思うのですが・・・。
皆さん方が学習してきたように、三角関数はまず直角三角形による定義をしますが、次に単位円による定義に拡張されます。その拡張された定義の元では三角関数は「円関数」と呼ばれることもあります。従って、三角関数からどうしても三角関係を連想される方は、「円関数!!」と5回ほど唱えれば邪念が払われるかもしれません?
4: これは数学史の問題です。その手の本を紐解くと、①の紀元前 2000 年頃、エジプト人がピラミッドの建設で原始的な三角比(1年の最初の頃に習った三角関数)を使っていたとあります。
そして、今2年生の皆さんが習っている三角関数や加法定理は、②の古代ギリシャ時代には確立されていたというので驚きです。
なお、③の1740年ごろというのは、オイラーが次の公式を発見した記念すべき年です。
ei x=cosx+ isinx
実数の世界では全くの無関係のように思われていた指数関数と三角関数が、複素数の世界では親戚どころか兄弟であったことを意味する重要な式です。
この式は、大学の工学部や理学部等に進学すると数学で学びます。今の段階ではこんな式があるんだ・・・という理解で十分です。オイラーはスイス生まれの数学者で、人類史上最も多くの論文を書いた数学者であったと言われています。
5: これは直感で正解してほしいところですが、ある意味難問かもしれません。
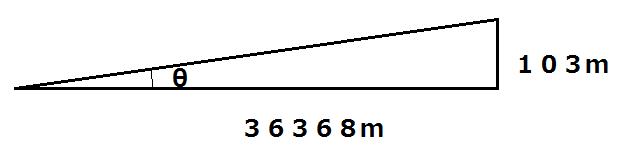
実際、人吉から八代方面に向かって国道219号線を車に乗っていると、道がずっとゆるやかな下り坂になっていることに気付くはずです。一体どのくらいの勾配なんでしょう?
これは、逆三角関数と呼ばれる計算をすることで求めることができます。
逆三角関数は数学では習っていないと思いますが、設計などの専門科目で学びますし、計算技術検定2級を受検した人にはおなじみのはずです。
Θ=tan-1(103/36368)を関数電卓に入れると、約0.16と表示されます。
6: 三角関数を単位円で再定義した際に、sinはy座標、cosはx座標になります。従って、第1象限と第3象限でsinとcosが等しくなることがありえます。
ちなみにこの問題は競技クイズ日本一決定戦の予選第1回戦(1問平均10秒のペースで解答する力が要求)に出題されました。
7: 頭の中に単位円を描き、30°、45°、75°それぞれのy座標をイメージしてください。30°のy座標と45°のy座標を重ね合わせた(足し合わせた)高さと75°の高さの比較になります。頭の中に図が丁寧に描ければ答は自ずと③と分かるはずです。
ここでは計算で求めてみます。
sin30°=1/2(=0.5)、sin45°=√2/2です。
ここで√2を約1.4として計算すると右辺は、
sin30°+sin45°=0.5+0.7=1.2
では、左辺のsin75°はいくらでしょう?
既に「加法定理」を学習した皆さんなら簡単です。
sin(α+β)=sinαcosβ+cosαsinβを使って
sin75°=sin(45°+30°)
=sin45°cos30°+cos45°sin30°
=(√2/2)( √3/2)+(√2/2)( 1/2)
=(√6+√2)/4
ここで、先ほどと同様に、√6を約2.4、√2を約1.4として計算すると、
sin75°=(√6 + √2)/4=(2.4+1.4)/4=3.8/4=0.95
従ってsin75°<(sin30°+sin45°)となります。
ここで覚えておいてほしいのは、
sin(α+β)=sinαcosβ+cosαsinβ
であって、
sin(α+β)=sinα+sinβ
にはならないということです。
では、この問題は加法定理を知らないと解けないのでしょうか?
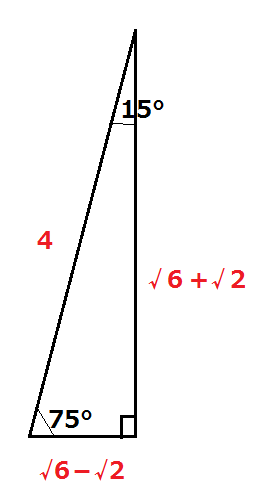
実は、75°と15°の右図のような直角三角形では、辺の比が「 4:√6 + √2:√6 - √2」というのが成り立ちます。
これを覚えておくと15°と75°について、sin、cos、tanの値が図を見ながら、sin75°=(√6 + √2)/4とか、たちどころに分かりますので非常に便利です。
某電力会社の就職試験問題で、sin75°=(□+√2)/4という穴埋め問題で、□に√6を入れさせる問題が出題されたことがあります。加法定理を万一忘れていてもこの辺の比を思い出せば楽勝です。
余談ですが、sinとcosの加法定理そのものの証明が1999年(平成11年)の東京大学の入試で出題されました。「公式は証明してから使うべき」というメッセージなんだろうか、それとも「教科書の内容すら身に付いていないのに難しい問題集を解いている受験生に対する警告」なのだろうかとか色々騒がれました。出来も非常に悪かったそうです。勿論、皆さんは習ったばかりなので証明はバッチリですよね?
8: 余弦定理とは、a2=b2+ c2-2bc・cosAという形の公式です。
今、A=90°のときcos90°=0ですから、a2=b2+ c2となり、これは中学校で習った三平方の定理そのものです。
正弦定理とは、a/sinA = b/sinB = c/sinC という形の公式です。
ちなみに、正接定理と呼ばれているものはありません。
余弦定理を用いることにより、三角形の「2辺の長さとその間の角度」から「残り1辺の長さ」を求められます。また、三角形の「3辺の長さ」が与えられた場合に、すべての角の余弦が求められ、すべての「角の大きさ」を考えることもできます。これに対して、正弦定理は三角形の「1辺の長さ」と「2つの角の大きさ」が与えられた場合に、「残りの2辺の長さ」を求めることができます。慣れるまでどちらの定理を使えばいいのか悩むことがあるかもしれません。
9: これはどれを選んでもマルにします。あなたなら先生からどう言われたいですか?私、自分で解答を作りましたが、3つともとても気にいっています。
この問題の作問のヒントになったのは、「サイン・コサイン何になる・・・♪.」と歌詞の中に出てくる『受験生ブルース』でした。日本のフォークソングの源流を作った男と言われる高石友也の代表曲で、1968年(昭和43年)に大ヒットしました。今でいう「団塊の世代」が大学受験地獄(この言葉は今、死語かも?)を経験していた頃で、当時私は小学3年(9歳)でした。テレビやラジオから毎日のように流れるその哀しい曲を何度も聞いているうちに、サイン・コサインという数学用語がしっかりインプットされました。
高校になって初めてサイン・コサインを習い、「こんなの勉強して何になる?」とその歌詞の意味するところが分かったような気が私自身しましたし、誰でも一度はそう思うのではないかとか考え込んでしまいました。
そういえば、鹿児島県の伊藤祐一郎前知事が2015年(平成27年)8月、「サイン、コサインを女の子に教えて何になる?」などと発言してちょっとした話題になったことがありました。
「いろいろな人生の問題があるため、今の均一な教育の仕組みを変えた方がいい」との思いからの発言だったと釈明されましたが、知事もきっと『受験生ブルース』を聞いて育った世代なのかな・・・と思った次第でした。
私自身も昔、生徒指導部で交通係をしていた頃、多分通学自転車のマナーの悪さに憤慨したドライバーだったんでしょう。苦情の電話の中で「アンタの高校、サイン・コサインとか難しいことを教えなくてもいいから、信号の見方をきちんと指導してくれ!」と罵声を浴びたことがあります。悲しい思い出です。
10: 三角関数はまず直角三角形による定義をします。これはまさにその範囲です。図をよく見ながら丁寧に読み解いていくと必ずわかるはずです。
私は昔からこの図を見るたびに、「本当によく出来た図だな!」と思っていました。あくまでも、α、β、α+βがいずれも鋭角という制限付きではありますが、加法定理がこんなに分かりやすく図の中に表現できるなんて、ある意味凄いです。
是非、sin(α-β)やcos(α-β)が表示できる図も考えてみてください。
【校長】
球磨工の情報を発信中!
リンクはこちらから
学校情報
〒868‐8515
熊本県人吉市城本町800番地
TEL 0966-22-4189
FAX 0966-22-5049
E-mail
kuma-th@pref.kumamoto.lg.jp
熊本県教育情報システム
登録機関
管理責任者 校長 坂本道彦
運用担当者 ホームページ係