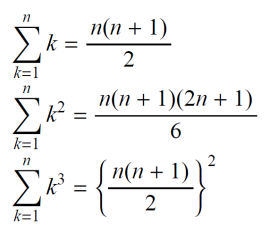３年生のあるクラス、２学期最後の数学の授業でa+biの計算をやっているのが廊下の窓越しに見えました。「想像上の数」を意味するimaginary number の頭文字iをとった虚数^＊1、まさにこの世に存在しない数です。高校の時にこの数に初めて触れた時のことを思い出しました。

そこで、今日、今年最後の掃除で校長室に来た機械科３年の生徒たちに、虚数についてのイメージや何のために複素数^＊2を学ぶと思うか尋ねてみました。「実在しない数をなんで勉強するの？」とか「どうせ将来使わないでしょ？」といった回答を期待して、話を深めていきたかったからです。

しかし、うまく真意が伝わらなかったのか、それとも突然ヘンな話題を振られてドギマギしたのか分かりませんが、虚数がこの世に存在しない数だということを理解していた人は確かにいたものの、今ひとつパッとしない感じの回答でした。あまりしつこく聞くと、最近はやりのマスハラ（mathematical harassment ：数学の証明を強要するなどして精神的な苦痛を与えること。たぶん）と言われかねませんので、クリスマスの楽しい話題^＊3に変えました。

前任校で数学の初任者研修会が開催されたことがあります。研究授業後の合評会で、多くの先生方が「数学の良さや楽しさ、数学が日常生活でどのように役立つのかを実感させることを心がけています」と仰っていました。しかし、学力差が激しいとされる数学の実際の授業の中では、「虚数単位『i』は、2乗すると-1になるという独特の計算ルールがあるだけで、それ以外はa,b,cのような普通の文字と同じように計算をすればいいですよ･･･」と指導するのが精一杯で、その数学的意義まで実感できるように指導することは難しいのではないかと思います。

よく、「交流回路の計算で使われる」という話が紹介されますが、具体的に計算式を示すには、まず電気についての説明が必要になります。改めてこの数を高校数学で取り扱うことの難しさを感じたところでした。

私自身は、高校１年の時に初めて虚数に出会いました。どういうストーリーの中でこの数が出てきたのかはっきり覚えていませんが、多分「２次方程式は、解を持つ場合と持たない場合がある。この2次方程式は実数解を持たない。でも、『解なし』じゃ困る。どうしても解がほしい。という中で、無理矢理『２乗すると-１になる数』を考えて解いてみましょう･･･」といった流れで学んだはずです。「何なのそれは？」と反応したかどうかも今では思い出せません。当時は今ほど数字に関する感性はなかったのだと思います。

　 数学史の本によると、虚数という言葉を初めて書物に書いたのは、「我思う、故に我あり」で有名なデカルト（1596～1650：フランスの哲学者・数学者）とされています。虚数が発見されてから数百年間は「詭弁（きべん）的な数字であり、実用性はない」「ただの想像上の数に過ぎない」と否定的に評価されていたそうです。ですが、オイラーの等式^＊4で有名なレオンハルト・オイラー（1707～1783：ロシアで活躍したスイス生まれの数学者・物理学者）が虚数のもつ重要性を解き明かした後、その評価は一変したようです。さらに研究が進むにつれ、その存在を仮定して計算に使ってみたら非常に便利であることが分かり、数学者の間で広く使われるようになったとありました。

ということで、数学者の方々にとっては非常に便利な数なんだそうです。でも、虚数が文字通り「虚（むな）しい数」にならないためにも、高校生の皆さん方にどのように有意義なのかということを示さなければならないとやはり思うのです。

そういう思いで、数学は何のために学ぶのかということをテーマにした様々な本に私自身目を通しているわけですが、ある本に次のようなとても興味深い記述があるのを見つけました。

　 「東に３iｍ進むということは北に３ｍ進むということ？　～ iをかけると９０度回転 ～」というタイトルの下、ざっと次のようなことが書いてありました。

私たちは中学校の数学で負の数（マイナス）を導入することにより、「西に３ｍ進む」ことを「東に-３ｍ進む」と表現することができるようになりました。

では、北に進むことを東に進むことを使って表現できないものでしょうか。

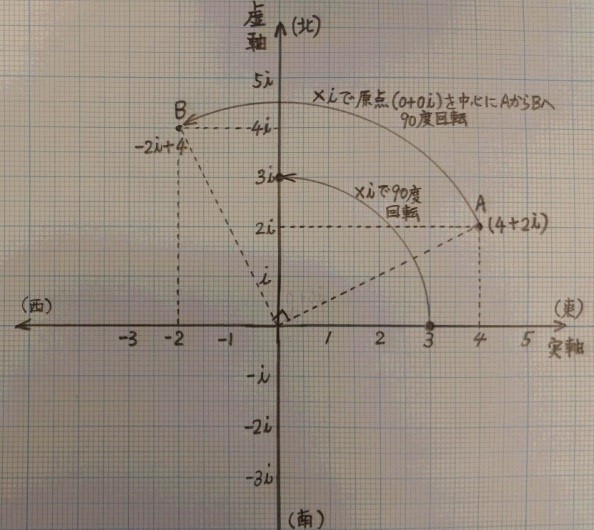
今、横軸が実数部分、縦軸が虚数部分を表す「複素平面」と呼ばれる平面を考えてみましょう。その平面上で「4+2i」の表す座標と、「4+2i」にiをかけた (4+2i)×i =-2+4i 即ち「-2+4i」が表す座標を比べてみましょう。

iをかけた後の点Ｂは、iをかける前の点Ａを「原点を中心に反時計回りに９０度回転させた」座標にあることがお分かりだと思います。

・・・・・・略・・・・・・

そういうことで、虚数iを導入することにより、「北に３ｍ進む」ことを「東に３iｍ進む」と表現することができるようになります。

このような説明を虚数について初めて学んだ高校１年の時に受けていれば、幽霊みたいなこの数もきちんと居場所ができて、よりとっつきやすく楽しく学べたのではないかと思っています。

　前置きが随分長くなりました。それでは本題です。

「２０１７を振り返る」　第１話

３年生の皆さん、習ったばっかりの複素数の計算です。長い前置きもそのためのものだったわけですが、次の計算をしてみてください。

　 (44+9i)(44–9i)＝【　　　】

 　２０１７になれば正解です。

ちなみに掃除に来ていた生徒たちにもこの計算に挑戦してもらいました。６人全員ができてホッとしました。

２０１７は素数であり、素因数分解はできませんが、このように複素数の範囲まで拡張すれば「素元分解」ができます。ちなみに、和暦の平成２９年も次のように

　29＝(5+2i)(5–2i)

分解できます。

今年は、西暦も和暦も素数で、６年ぶりのダブル素数ということで、年明け頃、素数ファンは大いに盛り上がっていましたが、「素数は素因数分解できないからつまんない･･･」なんていう声もチラホラ聞こえていました。しかし、4k+1型の素数はこのような形に分解できるのです。

このことについては、５月１１日の徒然雑記帳でも既に紹介していますが、あえて複素数の計算を習った直後の皆さん方に、この式を計算してもらい、行く年２０１７を偲んで欲しいと思い、再び話題にしました。

「２０１７を振り返る」　第２話

　右の年賀状は、今年の初め、日本数学検定協会から前任校に届いていたものです。２０１７をテーマとした面白い作問です。当時の生徒たちとかなり盛り上った思い出があります。

　皆さん、答は分かりますか？

 　「１つとって」と指示してありますが、それを無視してとりあえず全部の和を計算してみましょう。

　 １^３+２^３+３^３+４^３+５^３+６^３+７^３+８^３+９^３

＝1+8+27+64+125+216+343+512+729

＝2025　･･･①

　総和を2017にしたいわけですから、

2025－2017＝8＝2^３

よって、とり除くのは２^３です。

　簡単な問題ですが、これは足し算が全部で９項しかないので、このように実際に計算しても手間はたいしてかかりませんが、項数が多くなると大変です。

そこで数列の和を求める公式の登場です。

シラバスによると、本校では数列は習っていないようですが、右のように代表的な３つの公式はそんなに難しい形をしていません。３乗和の公式（上から３つめの公式）を使えば、第９項目までの和ですから、nに９を代入して、①の2025は次のように一発で出ます。

 　{(1/2)×9×(9+1)}²＝45²＝2025

それでは皆様、Merry Christmas！

【校長】

^※1,※２　この記事をお読みの中学生の皆さん方は、「虚数」とか「複素数」は初めて耳にする用語かもしれません。複素数は、皆さんが普段使っている「1」や「3」といった実数と「i」や「5i」といった虚数を組み合わせたもので、「－4+6i」や「5－12i」のように「〇＋△i」で表すことができる数を指します。虚数が現実に存在しない数なので、虚数を含んでいる複素数も現実には存在しない数です。

^※3　思い出のクリスマスプレゼントを聞きました。朝起きたら、綺麗にラッピングされた算数の問題集が枕元に置いてあったと･･･某君が。驚きました。毒サンタですね。

^※4　 オイラーの公式とは次の公式です。　ｅ^{i x}＝cosｘ+ isinｘ　

実数の世界では全くの無関係のように思われていた指数関数と三角関数が、複素数の世界では親戚どころか兄弟であったことを意味する重要な式です。大学の工学部や理学部等に進学すると数学で学びます。今の段階ではこんな式があるんだ･･･という理解で十分です。

電気、電波そして物質を構成する電子なども含めて、自然界は波や振動で溢れています。この波や振動現象を調べるためには、三角関数が必要不可欠です。オイラーの公式は、三角関数と指数関数が、虚数・複素数を通じて表裏一体の関係にあることを示しており、この公式を使用すれば、波動・振動現象に関して明確な答えを出すことができます。ちなみに、eはネイピアの数と呼ばれ、e = 2.718281828･･･の値を持ちます。

多くの数学者がこの公式を「人類の至宝」「人類史に残る不朽の名作」となどと表現しています。ちなみに、2004年に第１回本屋大賞を受賞した小川洋子著の小説「博士の愛した数式」（映画化もされました。本校の図書館にあります）の中では、θ=πのときのe^iπ = − 1、即ちe^iπ +1= 0という形で、博士が数学の中で最も美しい公式として愛していたという設定で登場します。

確かに、解析学・代数学・幾何学という異なる分野において定義された全く起源の異なる3つの数「e, i ,π」が、「1」と「0」という数学の基礎となる数とシンプルな1つの式で結び付けられており、式の意味はよく分からなくてもその美しさに感動します。