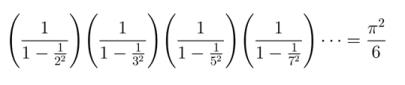徒然雑記帖
アクセス数 700000 → 0に思いを馳せる
暑中お見舞い申し上げます。
月が変わり、8月に入りました。連日厳しい暑さが続いていますが、生徒の皆さんをはじめ、いつもHPにお越しの皆さまには、健やかにお過ごしのことと存じます。
さて、校内では3年生が「夏を制する者は受験を制す」の心意気で、熱気に包まれながら学習会に参加する一方、部活動では先週の日曜日に、野球部が玉名工業高校と、バレー部は宮崎県の小林高校と練習試合を行うなど、新チームの選手たちが懸命に汗を流している様子を目にしました。
また、福岡市のマリンメッセで行われた玉竜旗大会に出場した剣道部からは、5回戦で敗れたという報告を受けました。「そこまでよく頑張った」と思いつつも、先日の高校野球でもそうでしたが、勝ち続けることの難しさを実感します。
カヌー部は、山形で行われるインターハイに向けて4日に出発します。いい結果を期待しています。

この花、早朝に咲き夕方にはしぼむので、儚(はかな)いものの象徴とされることもありますが、この猛暑の中に毎日毎日咲き続け、生命力を感じます。淡いピンクの涼しげな花びらの色合いが気に入っています。花言葉は「信念」で、お隣の国、韓国の国花でもあります。
ところで、昨夜、午後11時47分現在のアクセス件
とても感慨深いものを感じながら、素因数分解をしてみました。
700000=25×55×7
従って、その約数は、1,2, 4, 5, 7, 8, 10, 14, 16, 20, 25, 28, 32, 35, 40, 50, 56, 70, 80, 100, 112,125, 140, 160, 175, 200, 224, 250, 280, 350, 400, 500, 560, 625, 700, ・・・・(途中略)・・・・, 43750, 50000, 70000, 87500, 100000, 140000, 175000, 350000, 700000
の72個あることになります。
このような綺麗な数字をみると、数字の並びをそのままにして、加減乗除等の記号を入れ、意味のある数字を作ってみたくもなります。今回はこの記念すべき70万件*1を達成した昨日、8月1日の「81」という数字に挑戦してみます。
15分程色々やってみました。しかし、0の前後に+、-、×、÷をどう入れても無理です。所詮、ゼロはゼロです。
本屋さんには、「0から1の発想術」などの自己啓発本が溢れていますが、昔から「無からは何も生じない(From nothing, nothing comes.)」などと言われ、「無から有が生じることはありえない」とされているわけで、そのことを実感しながら無力感に苛(さいな)まれかけました。
しかし、数学の分野では、0にある演算を施して1を作る方法*2が幾つかあります。それを駆使して、絶対できるとの「信念」を持って精一杯悪あがきをしてみました。
70+{(0!+0!+0!)!}!!!!-0!=81 → 8月1日
【注】 中学生の皆さんへ。もう何度も説明していますが、”!”は「階乗」または「ファクトリアル」と読み、例えば5!なら、5×4×3×2×1を計算して120になります。
驚くかもしれませんが、0!=1です。これは定義(決めごと)*3です。ですから、「なぜ0!=1になるのか証明してください」と言われると困ってしまいます。このように決めると色々と都合がいいかからで、なぜ都合がいいかは高校の数学で学習します。
そういうことで、(0!+0!+0!)!=3!=6という所までは大丈夫だと思います。その後の”!!!!”というのが初登場になります。これは「4重階乗」と呼ばれるものです。
このような「多重階乗」は、高校の数学の範囲を超えますが、「2重階乗(ダブルファクトリアル)」や「3重階乗(トリプル ファクトリアル)」から順を追って説明します。決して難しいものではありません。ついて来てください。
・まず通常の階乗です。6を例にとると
6!=6✕5✕4✕3✕2✕1=720
・これに対して、2重階乗(!!)は階乗の1つ飛ばしバージョンと考えてください。
n!!なら、n×(n-2)×(n-4)×・・・×・・・というように、2つずつ減らしながら掛け合わせます。nが偶数だと×4×2で終わりますが、nが奇数だと最後は✕3✕1で終わることになります。
従って、 6!!=6×4×2=48 となります。
・3重階乗は階乗の2つ飛ばしバージョンです。n!!!なら、n×(n-3)×(n-6)×・・・ということです。最後は最小自然数まで掛けることになります。
従って、 6!!!=6×3=18 となります。
・もう大丈夫と思います。今日出てきた「4重階乗」は階乗の3つ飛ばしバージョンです。これも最後は最小自然数まで掛けます。
従って、 6!!!!=6×2=12 になります。大丈夫でしょうか?
結局、今日の式は、70+12-1=81ということの大袈裟な表現です。(^^
今日は0(ゼロ)に苦戦したわけですが、生徒の皆さん方は0にどのようなイメージを持っていますか。
「甘い飲み物なのになぜカロリーゼロ?」とか思ったことはありませんか?(本当は怖い「0カロリーの恐怖」なんていうテレビ番組を見たことがあります。ぞくっとする位、怖かったです)
3年生なら、求人票の中の「過去3年の採用・離職者数」の欄を見るはずです。離職者数が0だったら「この企業、きっといい職場かも?」とか高評価をつけるかもしれません。
私は、「残業ゼロで年収600万円」という見出しの記事を読んだことを思い出します。神奈川県内にあり、ワイヤーカット加工機で金属加工を営む社員7人の中小企業の実践例でした。経営者が作業工程や就業形態を見直し、残業代として払うべき賃金を基本給に組み込んだ結果、無駄の排除に取り組むなど従業員のモチベーションが格段に上がり、22時までの残業が当たり前だったのが、定時退勤に加え、社員全員に賞与(ボーナス)も夏・冬100万円ずつ支給、週休3日を検討中というように、劇的に就業環境が変わったとありました。違法な長時間労働が問題視され、働き方改革が広く議論されている中、「残業を前提にすると作業が遅くなる」という経営者の言葉が胸に響きました。また、つい最近、「住宅ローンの金利(利率)が0」という広告を目にしました。利用者からは勿論大歓迎でしょうが、銀行側からのメリットが何なのか疑問に思ったところです。
このように「特別な意義」を感じる「数としての0」です。一体誰が0を発見したのか?皆さんもきっとどこかで聞いたことがあるように、古代インドの数学で「0」の概念が確立されているようです。この夏、数学史の本を読んでみるのも一興かもしれません。
【校長】
*1桁が3桁違いますが、7月31日のニュースで、東京ディズニーランドが1983年4月15日に開園してから34年108日目で入場者数が7億人を達成したと報じていました。7億番目のゲストには、認定証や2020年まで有効の特別ご招待券などがプレゼントされたとか。こういう記念すべき数字にこだわる感性が強いのは日本人だけなのでしょうか?
*20から1を作る数学の演算、0!=1 の他にも cos0=1 とかあります。cosは「コサイン」と読み、高校1年で履修する数学Ⅰの三角関数の分野で学習します。
*3ちなみに、7月10日の記事の注釈で紹介した「どんな数字でも0乗すると1」については、厳密に言うと0だけは相手にしていません。0の0乗、即ち00は、0÷0と同様、不定ということで定義していないのです。
ただし、00=1と(暗黙的に)定義して議論を進める数学の分野も一部あるようで、Googleなどで「0の0乗」と検索すると「1」と主張するサイトに沢山ヒットします。色々悩ましいところですが、少なくとも高校の数学の範囲内では定義しないと考えておいていいと思います。
アクセス数689730 → 402人の皆さんにメッセージ
酷暑の中に体験入学が行われました。熱中症の発生を心配し、各所に給水所を設けたこともあり、体調を崩す方が出ることもなく、お昼過ぎに無事に閉校式が行われました。
閉校式を見届け、校長室に戻りHPを開いたら、午後0時18分現在のアクセス件数は、689730
「これはすぐにできるじゃない!」と思いながら、いつものように、数字の並びをそのままにして、加減乗除等の記号を入れてみました。
68✕9-7✕30=402
402とは、本日の体験入学に参加していただいた中学生の皆さんの人数です。暑い中に人吉・球磨だけではなく、遠方からもご参加いただきありがとうございました。
私たちは、「将来、橋を架ける仕事に携わりたいから、本校の建設工学科で学びたい」とか「発電所で電気を作って世の中に貢献したいから、電気科で学びたい」といった、目的意識を高く持った中学生の皆さんに一人でも多く入学してもらえればという願いを込めて、今日の体験入学を企画しました。
「目的意識」、これは中学3年になって最もよく耳にする言葉になっているはずです。これから志望校や学科を決定していくと思いますが、今日見たり聞いたりしたことが参考になれば幸いです。
また、今日は、およそ200人の本校生が、説明や案内、給水等で参加してくれました。自分たちの後輩を迎える為とはいえ、貴重な夏休みの1日にボランティアとして参加して、中学生のお世話をしていただきましたことに感謝します。
特にそれぞれ3年生にとっては、これからが正念場です。そんな皆さん方に俳句を一つ紹介します。
中学生の皆さんも本校生もこれから夏休みが本格化し、特にそれぞれ3年生にとっては、これからが正念場です。そんな皆さん方に俳句を一つ紹介します。
今日も太陽がぎらぎらと照り付け、積乱雲(俗に入道雲)*1がモクモクと立ち昇っています。夏本番です。皆さん方は、青空にくっきりと力強く湧き上がる入道雲を見てどのように感じますか。夏雲の湧きてさだまる心あり
これは本県出身の俳人である中村汀女*2によるもので、83歳の時に母校の第一高校の創立80周年を記念して建立された句碑除幕式で披露された俳句です。母校においでの汀女先生が、次のように在校生に語りかけられたようです。
【以下は、同校の80周年記念誌からの抜粋です】
「・・・白い湧きたつような夏の雲を見ながら(今は東京に住んでいますが)、私の心の一隅には熊本の夏雲があります。あ~もう夏になったなあ、といふ気持ちの中に、何か心に期するものがあるはずだ、思ひ立つことは実行することだ、そういふ気持ちが湧くといふ気持ちでしょうか・・・」
確かに、モクモクと高く湧き上がり、迫力のある入道雲を見ていると、自分の心の中に何か確かな志、強い決心のようなものが湧き上がってくるのを感じますよね。この夏、将来の目標を胸に秘め、本校を目指して受験勉強に打ち込んでいる中学3年生、そして決意新たに部活動や進路実現に向け汗を流す本校生に贈りたい句であると思い、ここで取り上げました。
夏休み中に、空を見上げて入道雲が目に入ったら、この句のことを思い起こしていただけると嬉しいです。
【校長】
*1積乱雲は、地上付近と上空の温度差がもたらす大気の不安定によって生じる雲で、その高さはゆうに10キロメートルを超え、成層圏まで達することもある。大雨や雷、竜巻など激しい気象の変化を伴うことが多く、俗に雷雲と呼ばれることもある。積乱雲は条件が整えば季節に関係なく発生する。一方、入道雲は夏に発生した積乱雲を指す場合が多い(入道雲は夏の季語)。なお、入道雲の「入道」とは仏道に入ることを意味し、入道雲のモクモクした部分の一つ一つが坊主頭のように見えるところから名付けられたといわれている。
*2中村汀女(なかむら ていじょ) 1900(M33)年~1988(S63)年、熊本県出身の昭和を代表する女流歌人、1980(S54)年文化功労者、1984(S59)年、日本芸術院賞受賞、名誉都民、熊本市名誉市民
アクセス数682962 → 鵯(ひよどり)越えの戦い
長い1学期が終わりました。明日から夏休みということで、生徒の皆さん方、心なしかウキウキしているようにも見えます。
そのような中、1学期最後の生徒会ボランティアとして、
私も生徒たちと一緒に汗を流し、校長室に戻り、ホッとしながら何気にHPを見たら、午後2時3分現在のアクセス件数は、682962
この数字にとても閃(ひらめ)くところがあり、数字の並びをそのままにして、加減乗除の記号を入れてみたくなりました。
6!+82-96÷2=1184 (今回は偶然にいとも簡単にできました!)
【注】 中学生の皆さんへ
もう何度も書いていますが、式の中にある"!"は「階乗」または「ファクトリアル」と読み、詳しいことは高校の数学で学習します。ここに出てくる6!なら、6×5×4×3×2×1を計算します。このようにn!なら、n×(n-1)×…×3×2×1の自然数の積を計算します。
「ひよどり越え」と1184の関係

私、赴任直後からなぜこの坂を「ひよどり越え」というのか、ひよどりが坂の上空を飛んでいる様子を想像しながら疑問に思っていました。
というのも、これは平家物語の中に「鵯越えの戦い」という名で描かれた、今から835年前、即ち1184年*3に実際に行われた源平合戦の一コマだからです。(以下、歴史に興味がない人も読んでもらえれば嬉しいです!)
鵯越えの戦いとは
寿永3年(1184年)2月7日、源平の戦いにおけるハイライトの一つ「一ノ谷の戦い」が始まりました。職員室にあった山川の日本史の教科書には「平氏追討軍の義経は、摂津の一ノ谷で大勝し、さらに平氏を西国に追い詰めていった」というようにさらっと書いてありましたが、私が高校のとき習った日本史の教科書には多分詳しく載っていたのでしょう。劣勢になった平氏が壇ノ浦の戦いで滅びる過程の戦(いくさ)の一つとして「一ノ谷の戦い」を詳しく教わった覚えがあります。「一ノ谷の戦い」は、源義経(みなもとのよしつね)が「鵯越の逆落とし」を行った戦いとして覚えています。
今回この記事を書くに当たり改めて調べてみると、一ノ谷は兵庫県神戸市須磨区に所在し、その古戦場跡は須磨浦(すまうら)公園として整備されていることが分かりました。また、鵯越町も隣の兵庫区内に実在し、鵯越小学校、神戸電鉄鵯越駅のようにその名が今も残っています。

本校や隣の人吉西小学校が所在する村山台地(高台)から人吉市街を見下ろし、「ひよどり越え」も写っている左の写真をご覧いただきながら、村山台地に源氏軍が陣取り、下手にあたる人吉駅当たりに平家軍が陣取ってにらみ合っている構図を想像してみてください。人吉駅の少し先には球磨川がありますが、そこは海(瀬戸内海)だと思わなければなりません。
台地から見下ろすと断崖は急坂で、馬に乗ったまま平家軍を攻めることは無理そうです。そこで源氏軍を率いる源義経は、どのような戦術をとったのか・・・。
義経は地元の猟師に「鹿が通れる道はありますが、馬はちょっと・・・(無理)」と聞き、「鹿が通れるなら馬が行けないわけがない!同じ四足(よつあし)ではないか。突撃!!」と号令をかけ、義経のあとには三千騎が続き、人馬もろとも怒濤(どとう)の勢いで急斜面を一気に駆け下がり、油断をしていた平家軍の背後をつき源氏軍を勝利に導いたのです。こんな会話が聞こえてきそうです。
「義経様!どうされますか?」
「この崖を・・・降りる」
「!!??」
「この崖を一気にかけおり、奇襲をもって平氏軍を打ち倒す!」
「義経様!そ…、それはあまりにも無謀では。この急斜面、馬で降りれるものでしょうか!?」
「無謀ではないぞよ。鹿がこの崖を降りていると聞いた。鹿が降りれるのに馬が降りれぬわけはない。ゆくぞ!」
「よ…、よしつねさ・・・」
「いざ!皆の者!ゆけ~い!!」
「うおおおおおお!!! バカッバカッ バカッ バカッ !!!!」
これは、私が高校の時の日本史の先生の口調を思い出しながらテープ起こしをしたものです。登場人物の声色を使い分け、身振り手振り交えて面白おかしく漫才のように演じてくれる先生でした。最後に口癖のように「きっとそんな会話があったのかもしれません・・・」とおっしゃり、現実に引き戻されていました。
そんな授業を受けると嫌が上でも記憶に残るもので、事実40年経っても覚えています。この流れからして、最後は次のように締めくくられたはずです。
平家の慌てぶりは尋常ではなく、弓や矢を取ることもなく、他人の馬に乗ったり、つながっている馬に乗ったりして、とても武士とは思えない体たらくで、散り散りになって海に向かって逃げて行ったのでした。
我先に船に乗り込んだことから、定員超過で沈没する船が続出、先に乗り込んだ者があとから乗ろうとする者を切りつけるなどしたため、海岸は赤く血に染まったことは言うまでもありません。これが前代未聞の奇襲「鵯越の逆落とし」であります。チャンチャン。
皆さんもそんな卓越した話術を持った先生に習うときっと歴史の授業が好きになると思いませんか?
話を戻します。こうして大打撃を受けた平家は瀬戸内海に追い込まれ、さらに西へ逃げ、勢いに乗る源氏はそれを追い、次のハイライトである屋島(現在の高松市のあたり)で再び戦い、そしてついに、1185年に壇ノ浦(本州と九州の間、関門海峡のあたり)で滅びるのです。
そういうことで、本校関係者は普通に「ひよどり越え」と呼んでいますが、そのような歴史*4を踏まえておくと、坂の名前一つでも味わい深いものがあるのではないかと思います。ただ、いつごろ誰があの坂を「ひよどり越え」と名付けたのか、人吉市史や本校の30周年記念誌などで調べましたが結局分かりませんでした。それどころか大変意外な事実を知りました。そのことについては、またいつかの機会に紹介します。
【校長】
*1 「ひよどり越え」を、測量サークルの生徒の皆さん5人に7月15日(土)に測量してもらっていました。それによると、一番下から一番上の段までの標高差は約40.136mで、全長153.41mでした。全部で365段の階段がありますから、1段当たり約11cmという計算になります。
一気に2~3段ずつ登れるところも多いので、高校生の足の実測値では登りに4分、下りで3分15秒といったところです。ただ、雨の日は滑りやすいので、安全のため1段1段踏みしめながら歩くのがいいのかもしれません。
*2 ひよどり(鵯)は、何で「卑」しい「鳥」なんていう字を書くのでしょう?ヒヨドリの生態が、字の成り立ちと関係があるのでしょうか?鳥の本で調べたところ、次のようにありました。
「鵯」の左の「卑」という字は、正確には「卑」の旧字体であり、古典語義で「低い」という意味を持ちます。「卑しい」の意味は「低い」から派生したもので、「背の低い鳥」という意味で「鵯」と書くのだそうです。
ひよどりは日本人には古くからの馴染みで、人に慣れるのも早く、平安時代の貴族たちが好んでペットにしていたとありました。ちなみに、英語ではbulbulと綴り「ブルブル」と可愛らしく発音する単語になります。
*3 「ひよどり越え」の清掃活動のまさにその最中、偶然にも下の駐車場に
*4 「鵯越えの戦い」の話は、困難に出会っても柔軟な発想で解決できるという教訓的な話でもあると思います。しかし、ある動物学の専門家が次のように語っています。「鹿と馬を同一と見るのは明らかな間違い。鹿は急斜面に対応できる身体をしているが馬はそんなことはない。そもそも蹄(ひづめ)の形が違う。重さも違う。まったく無理な話。鹿が通れるなら馬も通れるなどという話を信じたら大怪我をする。実際は鹿などが通る「ケモノ道」を見つけて、それを利用したに違いない・・・」と、にべもありません!「馬鹿」はこんなところに語源があるのかもしれないとか思ったところです。
等加速度直線運動の公式の憂うつ
先週の研究授業週間中、2年生の物理基礎では、実験をとおして等加速度直線運動を学習していました。
レールとビースビ(ラップタイムを計測する機器)2個を配置した木材を実験台の上に斜めに置き、小球を転がし、ストップウォッチで時間を計測して加速度を計算で求めるというものです。班ごとに協力しながら、実に楽しそうに実験をしていたのが印象的でした。
「自分が高校の時もこんな実験をしたのかな?」と、記憶の糸を手繰(たぐ)りましたが、結局思い出せませんでした。それどころか、これから導き出される様々な運動(自由落下、鉛直投げ上げ、鉛直投げ下ろし、水平投射、斜方投射)の数々の公式に苦しめられた辛い思い出だけが甦ってきました。
板書もしてあった次の3つの公式が基本になることは確かなのかもしれません。
① v=v0+at ② x=v0t+1/2at2 ③ v2-v02=2ax
ちなみに、②は、速度の式 v = v0 + atをv-tグラフに描き、グラフで囲まれた面積からも公式を導くことができますし、また、将来3年生になって微分積分を習うと、①と②の関係には、味わい深い関係があることが分かったのですが、当時はこの3つの公式すら、いい語呂あわせ、もしくは覚え方はないのかと恨めしく思っていました。しかも・・・
③は①と②からtを消去した式で、①からt = (v- v0)/a、これを②に代入して(数学が苦手な人にとっては少々面倒と感じるかもしれない)ちょっとした計算の末に得られます。手元の参考書には、「この③が最も覚える値打ちのある式である。時間を含まないで各量の間に成立する関係式を表しているので利用価値も高い。この式を覚えてないと、いちいち時間tを求めなくてはならなくなる・・・」とかあります。しかし、速度の2乗と初速度の2乗の差が、変位(移動距離)に加速度を掛けたものの2倍になるというが、(直感的に)どういうことを意味するのか今でもよく分かりません。
2年生はついこの前終わった期末考査の数学で、三角関数の加法定理など沢山の公式に苦しんだはずです。そういうことで、「杞憂であればいいけど、物理嫌いが出てこないといいけどな・・・」とか思いながら、参観した次第でした。
【校長】
アクセス数666666 → 今日はオイルの日

ありがとうございます。
666666とは、本日7月10日(月)15時57分現在の本校のHPのアクセス件数です。こういう綺麗な数字を見ると、数字の並びをそのままにして、加減乗除等の記号を入れてみたくなります。
朝のテレビで今日は「納豆の日」と報じていました。“ナナ”と“トオ”で納豆、なるほど笑わせます。でも、工業高校で学ぶ皆さんとしては、日本石油工業共同組合が定めた「オイルの日」(OILを半回転させるとそう見える)にも着目してほしい*1という願いを込めて、今日の日付の710を作ってみることにします。
666+6×6+6=708 (惜しい、2不足)
6!-6-6+6(6-6)=709 (あと一歩)
6!-{(6+6+6)÷6+6}=711 (あれ~今度は1オーバー)
(6+6)÷6+6!-(6+6)=710 (苦戦の末に完成)
ということで、今回は30分ほど考え込んでしまいましたが、やっと完成しました。できればスッキリです。必ずできるはずとの信念のもと、諦めずに挑戦する姿勢が大事ということかもしれません。
【注】 中学生の皆さんへ
(もう何度も説明しているところですが)2~4番目の式に出てくる"!"は「階乗」または「ファクトリアル」と読み、詳しいことは高校の数学で学習します。ここに出てくる6!なら、6×5×4×3×2×1を計算します。このようにn!なら、n×(n-1)×…×3×2×1の自然数の積を計算します。
ちなみに、2番目の式の中にある 6(6-6)は、60ですから1になります。どんな数も0乗すると1になります。高校の数学で詳しいことを学習しますが、今は約束みたいまのものと覚えておいてください。
ところで、666666を素因数分解すると、2×32×7×11×13×37ですから、約数は、1, 2, 3, 6, 7, 9, 11, 13, 14, 18, 21, 22, 26, 33, 37, 39, 42, 63,66,74, 77,78, 91, 99, 111, 117, 126, 143, 154, 182, 198, 222, 231, 234, 259, 273, 286,333, 407, 429, 462, 481, 518, 546, 666, 693, 777, 814, 819,・・・(途中略)・・・,15873, 17094, 18018, 20202, 25641, 30303, 31746, 37037, 47619, 51282, 60606,74074, 95238, 111111, 222222, 333333, 666666の96個です。
6のぞろ目の6桁の整数ですから、66や666で割り切れることは一目瞭然ですが、77や777で割り切れることは素因数分解するまで見破れず、意外な感じがしたところでした。
では、生徒の皆さん方に、今申し上げたことに関連した問題を出題します。
次の計算をしたら、答えはどうなると思いますか?直感(山勘)で次の三択の中から選んでください。
(666666×666666)÷(1+2+3+4+5+6+5+4+3+2+1)-
(777777×777777) ÷(1+2+3+4+5+6+7+6+5+4+3+2+1)=
①5555555 ②0 ③1234321
(答えはここには書きません。興味がある方は電卓をたたいてみてください!)
話は大きく変わりますが、皆さんは666666という数字を見て、どのようなイメージを持ちますか。
テレビのCMでよく聞く日本直販テレビショッピングの通販フリーダイヤル:0120-666666)を思い出した人もいるかもしれませんし、真ん中で切って、「666が2回連続している・・・」というのは、ごく普通の反応かもしれません。
では、その666だったらどうでしょう。何をイメージしますか。私なら・・・
○ 現在日本で流通しているコインの額面の和
500円硬貨+100円硬貨+50円硬貨+10円硬貨+5円硬貨+1円硬貨=666円
○ 最初の7つの素数の平方和(意外に有名です!)
666 = 22+32+52+72+112+132+172
○ 0から666まですべてを加算した総和は222111、0から666までのうち偶数だけを加算した和は111222(これも数学の雑学の本にはよく紹介されています)
などは明るく楽しい話題としてすぐ思いつきます。
しかし、666という数字は、実はキリスト教の新約聖書のヨハネ黙示録の中で、「獣の数字」として記されているらしく、悪魔や悪魔主義的なものを指す数字とされ、キリスト教徒にとっては13と並び大変忌み嫌われているようです。だからでしょうか、悪魔崇拝の組織は、この数字を使って様々な陰謀を企てているとか、とても恐ろしい裏の世界があるようです。ここで紹介するのはとても憚(はばか)られます。どうしても興味がある人は「666」で検索してみてください。数字の神秘に驚愕するはずです。
デジタル時計で111(1時11分)と目にしても、ぞろ目に特に関心がなければ何とも思わないかもしれません。222、333、444、555でもそうでしょう。でも666だったらどうでしょう。偶然にでも見てしまったら、多分背筋が凍り付くはずです。555の次のぞろ目は1111(11時11分)、2222(22時22分)しかあり得ないわけですから。
【校長】
*1 昔、機械科教師として教壇に立っていた頃、機械における潤滑油の働きを懸命に指導していました。現在のクルマのエンジンは、10万キロや20万キロ位はほとんどトラブルなく走れるほど優秀です。でもそれは、定期的なオイル交換を怠っていなければ・・・という条件のもとですから。
一般的に、機械の動きを良くするためには、物と物との摩擦を減らす必要があります。その役割として使う油(潤滑油:lubricant [ルーブリカント])は、機械をスムーズに動かすために欠かせない存在です。潤滑油には、機械の摩擦や摩耗を防止するだけでなく、機械のさびを防いだり、稼働する機械を冷やしたりする効果もあります。さらに、接触し回転する機械同士の隙間を埋める密封作用と呼ばれる効果もあります。
アクセス数654321→わが身世にふるながめせしまに
いつも本校のホームページにお越しいただきありがとうございます。

各桁の数字が綺麗に降順に並ぶこの記念すべき数に達するのは、8月11日頃か?と4月3日にアップした記事の中で予想をしていました。しかし、当時のアクセス数750件/dayの倍近い平均1350件/dayのアクセスが6月になって続いたこともあり、予想よりも40日以上も早く届きました。
ちなみに、654321*1は、各桁の数の和が21(3の倍数)ですから3で割り切れますので素数ではありません。しかし、こういう綺麗な数字を見ると、数字の並びをそのままにして、加減乗除等の記号を入れてみたくなります。どういう数字を作ろうかと悩みましたが、今年も半分過ぎたということで、今年の西暦2017を作ってみようと思いました。
65÷4+3×21=2007 (10不足!)
65×(43÷2―1)=2015 (惜しい、2不足)
(6!―54)×3+21=2019 (あれ~、今度は2オーバー!)
【注】 中学生の皆さんへ
3番目の式の中にある"!"は「階乗」または「ファクトリアル」と読み、詳しいことは高校の数学で学習します。ここに出てくる6!なら、6×5×4×3×2×1を計算します。このようにn!なら、n×(n-1)×…×3×2×1の自然数の積を計算します。
・・・・・・・・・・・・
数時間の格闘の後、ついにできました。「やっとできた!!!」と興奮冷めやらないうちに式を忘れないようにメモをしました。ところがです。何とその紙切れを誤ってゴミ箱に捨ててしまいました。焼却炉の中で灰になっているはずです。
色々思い出しながら何度も再チャレンジしましたが、結局できませんでした。こういうのを「再現性がない」と言って、理系の人たちは一番軽蔑するのかもしれないとか思いながら、今とても悔しい思いをしています。
話は変わりますが、新年を迎えると、その年の西暦を織り込んだ整数問題や年賀パズルを作ったり解いたりして楽しむ人たちがいます。
私は昔から小町算*2が好きなので、1から9の全ての数字をこの順に並べて加減乗除等の記号を入れてその年の西暦を作る問題に毎年挑戦しているのですが、これがなかなか苦労します。昨年は2017を作るのに、土日など全部で100時間位は費やしたはずです。苦労の末やっと1つだけできていました。これです!
1+2×34×5×6-7-8-9=2017
年が明けてネット上等で公開される全国の精鋭たちの美しい数式をみると、本当に凄い人がいるな・・・と毎年感心します。一例をあげます。
12+345×6+7-8×9=2017
-1×2+3÷4×5×67×8+9=2017(最初に-[マイナス]もokバージョン)
1+(2-3)×4×(5-6)×7×8×9=2017 (括弧もokバージョン)
9-8+7÷6×54×32÷1=2017(逆小町算と呼ばれています)
2018年が半年後に迫りました。生徒の皆さんも2018になる小町算に挑戦してみませんか?
紙と鉛筆があればすぐできます。モチロン、電卓があれば便利です。でも、なかなかうまくいかず、試行錯誤の連続になること間違いなしです。コツは30分やってみてできなければ、一旦全て白紙に戻して別のことをします。そしてまた次の日にやってみるのです。そうすれば意外にできたりします。完成したらすっきり気持ちがいいですよ!その快感・達成感を是非味わってほしいと思います。
私は既に1つだけ完成していますが(12×34×5+67-89=2018)これ以外で綺麗な式ができたら校長室に見せに来てください。一緒に観賞しながら努力を讃えあいましょう。
【校長】
*1「654321の平方根は何桁の数か」という問題を中学の時の数学で先生が問題に出してきたことがあります。皆さんだったらどう解きますか。確か次のような解き方で「3桁」を導くことを習った覚えがあります。
2桁×2桁の最大数=99×99=9801
4桁×4桁の最小数=1000×1000=1000000
654321はこの2つの数字の間にあるので3桁。ウンウン、なるほどそうきたか(^^)
*2本文の中にも書きましたが、「小町算」とは1から9までの数を1回と、+- × ÷ の計算記号を用いて、100の答えになる計算の式を作る遊びです。
このとき、1から9は順に並んでいることが条件です。34や789のような数も利用できます。きっと小中学校のときにやったことがある人がいるはずです。
下に解答例を紹介しますが、他のパターンを皆さんも頑張って考えてみてください。
12+3+4+5-6-7+89=100 (このような標準的なパターンで101通りあるそうです!)
-1+2+3+4×5-6-7+89=100 (最初にマイナスが付くことを許すパターンは61通り)
(1+23-4)×5×(6-7)×(8-9)=100 (括弧まで許すと一体何通り可能なんでしょう?)
1÷2×3×4+5×|6-7|+89=100 (さすがに絶対値は反則と言われるかも・・・?)
話は変わりますが、これがなぜ「小町算」と呼ばれるか御存知ですか?
小野小町(おののこまち)は、今から1200年程昔の平安時代の実在の歌人です。幼い頃から歌や踊りはもちろん、琴、書道となんでも上手だったそうです。絶世の美女だったそうで、我が国では、エジプトのクレオパトラ、中国の楊貴妃(ようきひ)と並んで「世界三大美人」と称されることでも有名です。しかし、小野小町が実際に小町算を解いたかどうかは定かでありません。それなのになぜ「小町算」と呼ばれるのか・・・?
いくつか語源が考えられているようですが、小野小町が深草少将(ふかくさのしょうしょう)に「自分のもとに100夜続けて通えば結婚してあげます」と約束し、その男性が99夜通って、あと1夜というところで亡くなってしまった! という話にちなんでいるという説が有名です。
また、美しくならんだ数字を計算すると、これまたきれいな数字の結果(100)が出てくるというのは感動さえ覚え、昔の人(小町算は江戸時代の寛保年間[1743年]には既に知られ、そう呼ばれていたそうです)は、そこに絶世の美女、小野小町を彷彿(ほうふつ)したのかもしれません。
100は確かに綺麗な数ですが、完全(100%)という意味で好きな人は多いはずです。100点は何回取っても学校で勉強をする身にとっては嬉しい数字でから。
ちなみに、100(=102=62+82)は10の平方数であり、2つの平方数の和になります。即ち、直角三角形の3辺の比が3:4:5の2倍の6:8:10もピタゴラス数ということです。
生徒の皆さん、100は最初の9つの素数の和(100=2+3+5+7+11+13+17+19+23)とか、100は最初の4つの自然数の和でもある(100=13+23+33+43=1+8+27+64)とか知っていましたか?美しいだけでなく、色々と面白い性質をもった数でもあります。
でも、私は、「こんなものに没頭していると、いつの間にか年を取ることも忘れて、おばあさん(おじいさん)になってしまうよ!」という警告であるという説が一番腑(ふ)に落ちます。ちょっと考えてみると、作る数が大きな数になればなるほど、式を作るのが難しくなってくることが予想されます。ちなみに、括弧や累乗を許さない標準的な小町算で1桁多い1000は、次の1通り(-12+34×5×6-7+8-9=1000)しかないと、コンピュータプログラムで解析したある同好家のサイトにありました。
そういうことを知らずにやっていると時間ばかり浪費するわけです。そのことを踏まえたうえでこの被虐的なネーミング「小町算」の由来を理解するには、百人一首にも取られている小町の次の和歌の知識が必要です。色あせた桜に老いた自分の姿を重ねた歌で、聞いたことがある人も多いはずです。
花の色は うつりにけりな いたづらに
わが身世にふる ながめせしまに
【現代語訳】
桜の花の色は、むなしく衰え色あせてしまった、春の長雨が降っている間に。ちょうど私の美貌が衰えたように、恋や世間のもろもろのことに思い悩んでいるうちに。
【鑑賞等】
【ながめせしまに】「眺め」は「物思い」という意味と「長雨」の掛詞(ダジャレ)で、「物思いにふけっている間に」と「長雨がしている間に」という2重の意味をかけています。
栄え咲き誇った桜の花も、むなしく色あせてしまったわね。私が降り続く長雨でぼんやり時間をつぶしているうちに。(かつては絶世の美女よ、花よと謳われた私も、みっともなく老けこんでしまったものね。恋だの愛だの、他人との関わりのようなことに気をとられてぼんやりしているうちに)
【現代語訳等の出典http://www.rakuten.ne.jp/gold/ogurasansou/hyakunin/009.html】
小町算以外にも「111×111=12321」(答えが1・2・3・2・1)なども面白い計算ですが、それはまたいつかの機会に。
アクセス数640221 → 考査1週間前
今朝5時15分現在のアクセス件数は、640221
数字の並びをそのままにして、加減乗除等の記号を入れてみたくなりました。
(64+0)÷2―21=627
627(6月27日)とは期末考査が始まる日で、今日(6月20日)はその1週間前です。部活動も「学習時間の確保」に配慮して早めに切り上げることになりますし、早朝の勉強会が始まった部もありました。
特に3年生は、考査後に計算する「評定平均」に一喜一憂するようになるでしょうし、それはそれで大事な姿勢かもしれません。
何はともあれ、納得いく結果が出るように、ラケットやバットをシャープペンに持ち替えて精一杯頑張ってください。
話は変わりますが、梅雨前線が北上して久々の雨です。傘を持って登校している生徒たちを見ながら、「さすがは球磨工生、天気予報のチェックの怠りはないな・・・!」と感心しました。
そして、明日6月21日は昼間が一番長い夏至。まだ、これから暑くなるのに、明日を境に日が短くなっていきます。まだ頂点と思っていない時に夏の頂点が来てしまい、小さく秋が始まることに、不条理感と言えば大げさですが、何かやりきれなさみたいなものをいつの頃からか感じるようになりました。生徒の皆さん方はいかがですか。
【校長】
616161 → 水無月
いつも本校のホームページにお越しいただきありがとうございます。
616161とは、月がかわった本日6月1日(木)11時15分現在のアクセス件数です。
「まるで今日の日を待っていたかのように616161とは何と縁起がいい!」とか考えながら、数字の並びをそのままにして、加減乗除等の記号を入れてみたくなりました。
61+61―61=61 → 6月1日 全く面白くありません。
6+1-6+|1-61|=61 → 6月1日 絶対値は反則なのかも?
(6-1)!÷(6―√16)+1=61 → 6月1日 今日の会心の出来!
【注】 中学生の皆さんへ
2番目の式の中にある"||"の記号は「絶対値」です。中学1年の数学で正の数、負の数を学習したとき、この言葉は見受けたことがあるはずです。数直線上の(原点との)距離(の差)を表し、|-4|=4とか学習しましたよね!
絶対値の問題では、絶対値の記号"||"をはずして計算をすることが多くあります。そのはずし方、3通りあります。
①絶対値の中が0より大きい場合は、|3|=3のように絶対値の記号をはずすだけ。②絶対値の中が0の場合は、|0|=0のように0になります。③絶対値の中が0より小さい場合は、|-4|=|(-1)×(-4)|=4のように、中の数字に-1をかけてから絶対値の記号をはずします。-をとるのではなくて、-1をかけるというのが"みそ"です。
先日、1年生のある教室の数学では、|√2-2|の絶対値をはずす授業をしていました。√2はおよそ1.414です。それから2を引きますので絶対値の中は0より小さくなります。従って|√2-2|=|(-1)×(√2-2)|=-√2+2(=2-√2)となります。中学生の皆さんにはちょっと難しいかもしれませんが、大丈夫ですよね!このくらい。
3番目の式の中にある"!"は「階乗」または「ファクトリアル」と読み、詳しいことは高校の数学で学習します。ここに出てくる(6-1)!即ち5!なら、5×4×3×2×1を計算します。このようにn!なら、n×(n-1)×…×3×2×1の自然数の積を計算します。
6月、あじさいが夢見心地に咲く梅雨(つゆ)の時期になります。雨音を聞きながら本を読んだり、眠りに落ちたりするのが好きな私は、6月は最も好きな月の一つです。
数十年前、中学で初めて古文を学習したときに、睦月・如月…という旧暦を暗記させられました。6月は水無月(みなづき)です。先生が「6月は雨がたくさん降る時期なのになぜ『水の無い月』と書くのでしょう?」と皆に問いかけられました。「確かにそうだよね」と思いました。
「水無月」の「無」は「の」にあたる助詞ですから、「水無月」は「水の月」ということになります。田植えが済み、田に水を張る必要があることから「水の月」→「水無月」と呼ばれるようになったといった趣旨の説明だったはずです。しかし、今日、ウィキペディア等で改めて調べてみたら、その他にも様々な説があるようです。
旧暦の6月は梅雨明け後で夏の盛りであることから、水が涸れて無くなる月であるという説
田植えなどの農作業をみんなやり尽した「皆仕尽(みなしつき)」が変化
雷が多いことから「雷月(かみなりづき)」が変化
そのように説明を受けると、どれも正しいような気がします。
睦月、如月、弥生、卯月、皐月、水無月、文月、葉月、長月、神無月、霜月、師走。旧暦に風情を感じるのは、その月にふさわしい呼び名だからかもしれません。大人(高校生)の常識として覚えておくべきことだと思いますが、生徒の皆さんは全部言えて、正しく漢字で書けますか?
そう言えば・・・、結婚当初、旅行に行く計画を立てた際、妻は「晴れるといいな」と、てるてる坊主をつり下げていたことがありました。「この人、こんなことをするんだ」と苦笑したことも思い出します。ジューン・ブライドでした。
最後に・・・、食中毒に注意しましょう。特にお弁当の管理!
【校長】
613557→5月28日(業平忌・辰雄忌)
今現在、午後2時5分現在のアクセス件数は、613557
数字の並びをそのままにして、加減乗除等の記号を入れてみたくなりました。
613-5!+5×7=528 → 5月28日
【注】 中学生の皆さんへ !は「階乗」または「ファクトリアル」と読み、詳しいことは高校の数学で学習しますが、例えばここに出てくる5!なら、5×4×3×2×1を計算することになります。このようにn!なら、n×(n-1)×…×3×2×1の自然数の積を計算します。
今回はあまりにも簡単に528ができあがったので唖然としましたが、今日5月28日と言えば文学忌*1の一つ「業平忌」です。
その話をする前に・・・
前任校で春休みの宿題に「あなたが一番好きな歴史上の人物を一人取り上げて、その生涯やどのような点が好きなのかレポート用紙5枚程度でまとめなさい」という課題を出される先生がいらっしゃいました。どのような人物が高校生に人気なのかと気になりました。大河ドラマに取り上げられていた平清盛とかかな?と思いながらレポートを見せていただいたところ、徳川家康が多く、意外だな・・・と思った記憶があります。
皆さんだったら誰を取り上げますか。私、今だったら在原業平(ありわらのなりひら)にするかもしれません。でも、業平をよく知らなかった(あまり関心がなかった)高校の頃だったら誰にしただろうとか考え込んだところです。
在原業平は、伊勢物語(本校では2年生の国語総合で2学期に学習する予定と聞いています)のモデルとされている実在の人物で、和歌に優れ六歌仙*2の一人でもあります。今から約1,200年前に生きたこの方、天皇の血を引く由緒正しい実在の貴族なのですが、既存の風習にとらわれず、56歳の生涯の中で多くの女性(一説には3,733人)と関係を持っていきます。一夫多妻制の当時の結婚形態を考慮に入れてもスゴイの一言ですが、別にそういう所に憧れるのではなく、反骨の精神で自由奔放に、そして風流に生きたその生き様に心惹かれるわけです。実は、今日5月28日はそんな業平の命日とされる日なのです。
業平が晩年を過ごした京都市小塩の十輪寺では、毎年この日に「業平忌」を営み、平安王朝時代の歌聖業平を偲んでいます。今年は日曜日に当たりましたが、10年ほど前、土曜日だった日にそのお寺を訪ねたことがあります。全国から集まった本堂に入りきれないほど沢山の業平ファンが境内から見守る中、住職が三弦を弾きながらお経(般若心経)を唱え始めると、木漏れ日に薫風が葉影を揺らす中、鶯(うぐいす)のさえずりだけが聞こえ、異空間に迷い込んだ気がしました。
彼が関わりを持った女性たちも、そのことで運命が分かれ、幸・不幸様々な人生を送ったに違いないと、胸に迫るものがあったことも静かに思い出しました。業平が生きた年月よりも1つ多く齢を重ねてしまった今、「貴方にとって恋愛とは何だったのか?」と訊いてみたい気がします。
話は大きく変わりますが、作家の堀辰雄が昭和28年5月28日、肺結核のため享年48歳で亡くなっており、今日は「辰雄忌」でもあります。
中には「堀辰雄なんて聞いたことないよ・・・」という人がいるかもしれません。でも、数年前に大ヒットした宮崎駿監督のアニメ映画「風立ちぬ」は見たことがある人も多いはずです。これ、実在の人物である堀越二郎をモデルにその半生を描いたものでしたが、堀辰雄の小説「風立ちぬ」からの着想が盛り込まれていたと知ると、きっと身近に感じるはずです。実際、映画のポスターには、「堀越二郎と堀辰雄に敬意を込めて」と印刷してありました。
余談ですが、「後期一般入試を受けて入学した1年生は、全員が堀辰雄の『風立ちぬ』*3の抜粋を読んで入学している」と言ったら、驚くかもしれません。
実は・・・
この3月に実施された熊本県公立高校入試の国語で、この「風立ちぬ」からの抜粋でしょっぱなの問題が作問されていたのです。「一朝一夕」にふりがなをつける問題がありましたよね!できていましたか?
そんなこんなでもうすぐ5月も終わり。衣替えの季節です。夏服への移行期間ということで、ざっと見て8割以上の男子生徒が白い開襟シャツを着ています。
高校総体もサッカーなど先行実施分が始まり、順当に勝ち進んでいるようです。保護者の皆さまには、暑い中ご声援をいただきありがとうございました。
学校の四季の中で皆さん方が一番輝く季節の到来です。文武両道で頑張ってください。 【校長】
*1文学忌(ぶんがくき)とは、作家の命日をその雅号やペンネーム、代表作などにちなんで、その文学的な業績を偲ぶ日としたものです。国文学の専門家の手帳のカレンダーには、文豪の文学忌や誕生日がびっしり書き込まれているとか聞いたことがあります。
もし、皆さん方の中に「桜桃(おうとう)忌」とか聞いて、「太宰治大先生!」とか言い出す人がいたら、相当なファンなのかもしれません。桜桃忌はもうすぐ6月13日、さくらんぼが美味しい頃です。
*2六歌仙(ろっかせん)とは、平安時代の勅撰和歌集(ちょくせんわかしゅう:天皇や上皇の命によって編集された歌集)である「古今和歌集(こきんわかしゅう)」の序文に名前が挙げられている 6人の歌人をいいます。具体的には、僧正遍照(そうじょう へんじょう)、在原業平(ありわらのなりひら)、文屋康秀(ふんやのやすひで)、喜撰法師(きせんほうし)、小野小町(おののこまち)、大友黒主(おおとものくろぬし)です。
試験で名前を問われることがあり、「大いに喜べ 小僧の分際(おおいによろこべ こぞうのぶんざい)」→【変換】大いに喜べ 小・僧の文・在 などと覚えたものですが、皆さん方はどのように暗記しているのでしょうか?
*3モチロン、「風立ちぬ」は「風が立たない」という打消しの意味ではなく、「あっ、風が吹いた!」という意味です。36年前、グリコ・ポッキーCM曲として松田聖子さんが歌った同名の曲が、後に爆発的にヒットしたことがありました。大学生だった当時、友達同士での「風立ちぬってどういう意味だろうね?」という会話の中で、何気に打消しで訳したところ、「あんたの文法、相当ヤバい!」と笑われたことがありました。
祝 アクセス数600000件達成
いつも本校のホームページにお越しいただきありがとうございます。
600000とは、5月19日(金)23時35分現在の本校のHPのアクセス件数です。
50万件を達成したのは、今年の1月30日(土)でした。従って、1日平均917件という県下の公立高校の中では最高水準のアクセスを日々いただきながら順調に数を増やし、109日(約3ヶ月半)で10万件を積み上げたことになります。
私が球磨工業高校の驚異的なアクセス数に気付いたのは、前任校に勤務していた平成27年10月頃で、20万件にもうすぐ届こうとしていた頃でした。当時から球磨工のアクセスデータを記録して、どうすればこのように多数のアクセスを頂戴できる魅力的なホームページになるのか分析していました。
それによると、本校のアクセス数は、次のような経緯をたどっています。
200000 2015年【平成27年】10月14日
↓
↓ 177days(1日当たり564件)
↓
300000 2016年【平成28年】4月8日
↓
↓ 157days(1日当たり637件)
↓
400000 2016年【平成28年】9月12日
↓
↓ 140days(1日当たり714件)
↓
500000 2017年【平成29年】1月30日
↓
↓ 109days(1日当たり917件)
↓
600000 2017年【平成29年】5月19日
ここでクイズです。現在のペースがあまり落ちなければ東京オリンピックの開催の年である(2020年【平成32年】)までに桁上がりして100万(1,000,000)件が到達できるのでしょうか?
ざっと暗算しても達成できることがお分かりと思いますが、一応電卓を叩いて確認してみます。
残り40万÷917=436日ということで、100万件の達成は来年、2018年【平成29年】の7月28日前後だと思われます。
ところで、600000という数字は、妙に惹きたてられるものがあります。素因数分解をしてみました。
600000=26× 3 × 55
従って、約数は、1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 25, 30, 32, 40, 48, 50, 60, 64, 75, 80, 96,・・・・・(途中省略)・・・・・, 40000, 50000, 60000, 75000, 100000, 120000, 150000, 200000, 300000, 600000 の84個あることになります。
そう言えば、私は名前が西で、その擬音語(onomatopoeia:オノマトピア)の数字表記である24(ニシ)で色々と遊んでいたら、次の面白いことに気付いていたことを思い出しました。
●とりあえず24の2桁を足してみます。
2+4=6
●24の約数を全部足してみます。
1+2+3+4+6+8+12+24=60 「アレっ!」
●24同士を掛けたり足したりしてみます。
24×24+24=600 「何とまぁ!!」
それ以来、この600000(60万)の弟的な存在である6、60、600にも愛着を持っています。生徒の皆さんは、それらの数字を目にするとどんなことを思い出しますか?人によってかなり違うと思いますが・・・、私がパッとおもいつくものをそれぞれ6個ずつ挙げてみます。
「第6交響曲」・・・くま川鉄道で土日に1日1本運行される観光列車「田園シンフォニー」ではベートーベンの交響曲「田園」をBGMで聴きながら美しい田園風景が楽しめます。普段の運行では流れていませんが、「日本一心豊かな通学列車」と言われるこの列車で約190人の本校生が通学しています)
「6×1023」・・・アボガドロ数(原子、分子、イオンなどの物質粒子1mol[モル]中に含まれるそれらの粒子の数:1年次の化学基礎で勉強します)
「6は完全数*1」・・・6=3+2+1
「6月の花嫁」・・・June bride(ジューン・ブライド:6月に結婚すると幸せな結婚生活を送ることができるという西洋の言い伝え)
「6は母性の象徴」・・・胎児をお腹に抱える妊婦のイメージ。暖かさ・優しさ
「6は西洋では悪魔の数字」・・・「悪い」や「無い」を意味する忌み数(不吉な数として忌避される数)であると聞きます。(日本の4「死」や9「苦」みたいなもの?)
「60進数」・・・1分は60秒、1時間は60分
「60Hz(ヘルツ)」・・・西日本地域の商用交流電源の周波数(電気のプラス、マイナスが1秒間に60回入れ代わっています。その入れ替わる回数を周波数(単位:Hzヘルツ)と言います)
「60度は(30度、45度とならぶ)有名角」・・・三角定規の角度でもあり、cos60°=0.5とか1年次の数学Ⅰで学習します。
「60兆個」・・・体重「60kg」の平均的男性の細胞の個数(割り算して細胞1個当たりの重さを計算してみたいと思う人は多いかも?)
「結婚60周年」・・・ダイヤモンド婚
「60歳からの人生の再設計」・・・還暦を迎え、定年退職した後の老後をどう楽しく送るかは国民みんなの課題
「600の前後の数599と601」・・・双子素数*2
「600円」・・・ 500円+100円(異なる日本円硬貨2枚で作ることのできる最大の金額)
「CBR600RR」・・・ホンダの600ccのスポーツバイク(昔、同僚の先生が乗っていました。ナナハン並みのパワーがあるとか。現在生産中止)
「600系 or 600形」・・・電車の形式(新幹線は欠番)
「TOEIC600点」・・・社会人が仕事と両立させながらとりあえず目指す点数
「年収600万円」・・・埼玉県では、30代は年収600万円あって「人並み」の生活ができる。(最近の朝日新聞の記事で印象に残っています)
【校長】
*1完全数とは、自分自身を除く正の約数の和に等しくなる自然数のことです。映画化もされた小川洋子著「博士の愛した数式」で話題になりました。
完全数の最初の3個は 6 (= 1 + 2 + 3)、28 (= 1 + 2 + 4 + 7 + 14)、496 (= 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248) です。ウィキペディアによると、「完全数」は「万物は数なり」と考えたピタゴラスが名付け親ということですが、彼がなぜ「完全」と考えたのかについては何も書き残されていないということです。何が「完全」なんでしょうか、気になっています。
*2双子素数とは、差が 2 である2つの素数の組のことです。小さい順に(3, 5), (5, 7), (11, 13), (17, 19), (29, 31), ・・・というように双子素数は無限に存在するように思えます。
ウィキペディアによると、素数が無数に存在することは古代ギリシャの時代から分かっていて、ユークリッドの『原論』にその証明があるんだそうです。これに対し、双子素数は無数に存在するかという問題、いわゆる「双子素数の予想」は、いまだに数学上の未解決問題で、「無数に存在するだろう」と多くの数論学者が予想しているということです。
ところで、(3, 5) を除く双子素数は (6n − 1, 6n + 1)(n は自然数)の形で表せるということに気付きましたか?
アクセス数592017にセミを思う
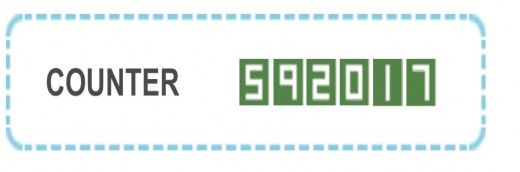
592017とは、5月11日(木)午前6時16分現在
の本校のHPのアクセス件数です。
ここ1週間の1日当たりの平均アクセス数720件のまま推移したと仮定して、「○○2017」というアクセス数が今年2017年の間に何回程あるのか気になりました。
482017・・・2016年12月28日(確定)・・・×
492017・・・2017年 1月15日(確定)・・・○
↓
↓
↓
↓
592017・・・2017年 5月11日(本日)・・・○
↓
↓
↓
↓
752017・・・2017年12月21日(予定)・・・○
762017・・・2018年 1月 5日(予定)・・・×
ということで、あくまでも仮定の下ですが、492017から752017まで27回出現することが予想されます。
この27回の「○○2017」の中で素数(中1で習ったように、その数と1でしか割れない数字: 2、3、5、7、11、13、17・・・など)はいくつあるのかとても気になり始めました。
末尾4桁の2017自体は素数*1ですが、その前に○○という2桁が付くとどうなるのかということです。昔から知られているように、素数の出方は神出鬼没で予測不能、求める公式はありません。「それら27個のうち3つ位は素数かもしれない」という予想の下、最初の492017から素因数分解をしてみました。
何でも分解しないと気が済まないのは、機械科の教員として染みついた悲しい性(さが)です。「おっと、いきなり最初から素数とは!」と、驚きつつも一つ一つ丁寧に計算していきます。
492017・・・素数!
502017・・・3×167339
512017・・・11×89×523
522017・・・素数!
532017・・・32×59113
542017・・・7×77431
552017・・・31×17807
562017・・・3×187339
572017・・・439×1303
582017・・・素数!
592017・・・3×197339
602017・・・13×46309
612017・・・7×17×37×139
622017・・・32×11×61×103
632017・・・23×27479
642017・・・223×2879
652017・・・3×217339
662017・・・19×34843
672017・・・29×23173
682017・・・3×7×47×691
692017・・・素数!
702017・・・素数!
712017・・・33×26371
722017・・・83×8699
732017・・・11×13×5119
742017・・・3×247339
752017・・・7×53×2027
ということで、5個ありました。6桁の数字から、ある意図を持って取り出した末尾7の数字27個の中に、素数が5個という出現率(19%)は、高いのか低いのか大いに気になったところです。
ところで、生徒の皆さんは、素数はランダム(でたらめ)に現れると思いますか。*2
実は、素数はアマチュアからプロまで多くの同好の士が研究の対象としています。素数が出現するランダム性について、アメリカのスタンフォード大学の数学科の先生方による次のような趣旨の研究結果を読んだことがあります。
最初の1億個の素数を調べた結果、「1で終わる素数」の次がまた「1で終わる素数」になる確率は18.5%で、本当にランダムならこの確率は25%じゃないとおかしい。一体何だ!!という趣旨の話です。
おわかりでしょうか・・・?
素数の末尾はかならず1、3、7、9なので、確率は4つに1つ即ち25%のはずです。この研究結果によると、100%ランダムに出現するのじゃなさそうです。試しに他の数字でも調べているようで、「3」と「7」で終わる素数が連続して出る確率は30%、「9」で終わる素数が連続して出る確率は約22%だったそうです。
面白いですよね!でも素数を相手に格闘していると、桁が大きくなるほど電卓片手とはいえ計算が大変です。次のようなことはよく知られた事実です。
1 数が大きくなるほど、素数の出現頻度が下がる。(素数の出現頻度は、桁数に反比例するのだそうです)
2 数が大きくなるほど、素数判定に必要な計算回数が増える。(経験上当たり前のことかもしれませんが、素数発見難度は桁数のほぼ3乗に比例するのだそうです)
ということで、622017=32×11×61×103 のように気持ちよくサクサクと素因数分解できたものもありましたが、○○2017のわずか27個が素数かどうかの判定計算は、電卓片手に本日(育友会総会代休)の大半を費やしました。
勿論、ネット上には、素数表や素数判定機、素因数分解計算機など便利なツールが沢山出回っています。今回は、素因数を見つけることができずgive upしてしまった572017に致し方なく使いましたが、数に対する感覚の鋭敏さを保つうえで手計算は大切だと思っています。
余談ですが、自分の生年月日が素数かどうか判定するアプリがあります。例えば、2001年7月17日生まれの人がいたとして、これを使うと20010717が素数かどうか一瞬で判定してくれます(この場合、32×17×31×4219と素因数分解でき素数ではありません)。
双子素数(11と13のように差が2の素数の組み合わせ)同士のカップルや2人の生年月日を足した数が素数になればラブラブとか・・・そんな嘘みたいな甘い言葉に誘われて私も色々と相性を確かめたことがあります。最近、何と1京未満(16桁以下)の自然数を対象とする素数判定機が登場し、12桁のマイナンバーが素数かどうか確認して一喜一憂する遊びに使っている人が多いと聞きました。マイナンバーのような12桁の数が素数になる確率はわずか3.8%(詳細は略しますが、「素数定理」を使って計算できます)です。ざっと計算して、1億2千700万人×0.038=483万人ですから、日本人のうち福岡県(約510万人)の人口にちょっと足りない位の人が素数のマイナンバーをもっていることになります。
私も自分のマイナンバーがどうなのか興味津々で使ってしまいましたが、素数ではなくて残念でした*3。そのうえ、個人情報が収集されてしまった可能性について考えが及ばなかったことに気づき、真っ青になったのは後の祭りでした。
話は大きく変わりますが、生徒皆さん、「素数ゼミ」って聞いたこと
北米には、ちょうど17年ごとと13年ごとに大量発生するセミ(蝉)がいて、17も13も素数であることから、「素数ゼミ」と呼ばれています。写真のように目が赤くて少し不気味な感じの日本では見受けないセミです。このセミたちは、普通のセミと同じように、一生の99.9%の長さを地中で脱皮を繰り返しながら幼虫のまま、木の根から養分を吸って過ごします。そして、誕生から17年又は13年が経った特定の年の夏がくると、幼虫はいっせいに地面から這い出します。
昨年2016年は、オハイオ州やペンシルベニア州などで17年ゼミが大発生しました。その数は、何と数十億匹で、電話の声も聞き取れないほどだったと、この珍事、日本でも大きく報じられました。なぜ17年周期と13年周期で大発生するのか、アメリカでは毎年その周期が来るたびに、多くの研究者が仮説をたてておられるようです。しかし、セミの生物時計がこれほどまでに正確な理由は誰も知りません。
この難問を解明し、生物界を驚かせた日本の研究者がいらっしゃいます。数理生態学が御専門の静岡大学の生物学者、吉村仁教授(静岡大学)です。幼いころは、昆虫採集に夢中な「昆虫少年」だったそうです。「素数ゼミ」の名づけ親でもありますが、セミのほかにも様々な動物の行動を進化的な数理モデルで解析されておられます。
世界中から注目された吉村教授の学説*4、「素数ゼミの謎」という著本に詳しく書いてあります。本校の図書館には入ってなかったようですので、司書の坂口先生に購入してもらうようにお願いをしておきました。
地球上にセミが登場したのは2億年以上も前なんだそうです。ちなみに、人類は約700万年前ということです。セミたちが生きるための進化とはいえ、興味が尽きません。関心がある方は是非、読んでみてください。
【校長】
*1今年2017年(平成29年)は、西暦の2017も和暦の29も素数です。6年ぶりのダブル素数ということで、年明け頃、素数ファンは大いに盛り上がっていましたが、「素数は素因数分解できないからつまらない・・・」なんていう声もチラホラ聞きました。そういう声を聞くと、意地と根性で因数分解をしてみたくなります。どちらも悪戦苦闘の末、どうにかできました!
2017=(9+44i)(9-44i)
29=(5+2i)(5ー2i)
勿論、iは虚数単位でi2=ー1です。このiを使った因数分解は反則でしょうか?
電気科の皆さんは、電気の計算において虚数が大活躍することは御存知のとおりです。電流を通常iで表記しますので、区別するために虚数単位はjを使っていますよね。
*2素数について深く研究した18世紀の数学者・天文学者である
オイラー(Euler)は、2、3、5、7・・・と続く素数について右
のような関係式を発見しています。不規則に出現する素数と円
周率の間に成り立つこの綺麗な数式に、オイラーは何を感じた
のでしょうか?
*312桁のマイナンバーが素数でなくがっかりした方に朗報です。マイナンバーは4桁区切が3つ合わさった12桁ですから、4桁ずつ吟味するという楽しみ方もあります。この4桁の素数の出現率は12%位ですから、3つ全部が素数となる確率はこれを3乗して0.17%です。これは本当にレアものかもしれません。
逆に、3つに分けたうち少なくともひとつが素数になるのは何%位でしょう。余事象(3年生の数学Ⅱで学習します)の考え方を使うと計算できます。興味ある方は計算してみてください。
*4ネタバレにならない程度の概要です。
生活周期が比較的大きな素数になっているのは、17年ゼミと13年ゼミの交雑する可能性が最小限になるからでは?これが先生の仮説です。たとえば、これが7と5という小さな素数だったとしたら、35年に一度、成虫になる時期が一致する。生活周期が長くても、たとえば16と12のように素数でない数だった場合、16年ゼミと12年ゼミが交雑する可能性は48年ごとに出てくる。
17と13のように大きな素数なら、両者が交雑する機会は221年に一度しか巡ってこない・・・
いずれが あやめ か かきつばた
 今日で4月も終わり。2017年も3分の1が過ぎたとか思いながら、どんな部活が日曜日に練習をしているかと学校に歩いて行きました。いつもは車で通勤しているので気付かなかったのですが、学校の北門へ続く上り坂の手前の道路際に紫色の花をつけた「あやめ」らしい植物(右の写真の黄色枠)が目にとまりました。
今日で4月も終わり。2017年も3分の1が過ぎたとか思いながら、どんな部活が日曜日に練習をしているかと学校に歩いて行きました。いつもは車で通勤しているので気付かなかったのですが、学校の北門へ続く上り坂の手前の道路際に紫色の花をつけた「あやめ」らしい植物(右の写真の黄色枠)が目にとまりました。そう言えば、これから6月にかけて、あやめ や しょうぶ や かきつばたのシーズンです。県内でも玉名市の「高瀬裏川花しょうぶまつり」や天草市の西の久保公園で開催される「天草花しょうぶ祭り」等がもうすぐ開催されるはずです。
ところで、生徒の皆さん。「いずれがあやめ か かきつばた」(「何れが菖蒲か杜若」)という言葉を聞いたことありますか。どちらも優れていて、選択に迷うことの例えで、あやめ と かきつばた はよく似ていて見分けにくいところから来た言葉のようです。
私自身、以前、あやめと しょうぶ と かきつばたの違いを調べていて混乱したことがあります。生徒の皆さん方は大丈夫ですか?
あやめ と しょうぶはどちらも漢字で書くと「菖蒲」です。しかし、漢字は同じでも菖蒲(あやめ)と菖蒲(しょうぶ)は全く異なる植物です。「あやめ」はアヤメ科、「しょうぶ」は何とサトイモ科なんです。
次に、菖蒲(しょうぶ)と花菖蒲(はなしょうぶ)も別物。花菖蒲はアヤメ科です。だから「あやめ」と「しょうぶ」と「はなしょうぶ」は、ぜぇ~んぜん違う植物です。
さらに、「いずれがあやめ か かきつばた」の杜若(かきつばた:これはアヤメ科)が加わって、まるで4つ巴(どもえ)の争い。頭がぐちゃぐちゃになるのです。
整理すると、5月5日の端午の節句の菖蒲湯に入れる①「しょうぶ」(菖蒲)、②「花菖蒲」、③「あやめ」(菖蒲)、④「かきつばた」(杜若)の4つは似ているようで、実は全然違うのです。
まず、①サトイモ科に属する①「しょうぶ」は、左の写真のように花の様相が全く違いますのでこれはいいでしょう。
植物学的にアヤメ科アヤメ属に分類される②「花菖蒲」、③「あやめ」、④「かきつばた」は同じ仲間だから似ていて当たり前。右の花の写真を見ても、「違いを覚えるのは無理!」と諦めたくなるほど微妙です。
そこでもっと調べていくと、③「あやめ」と②「花菖蒲」・④「かきつばた」を見分ける一つの手があることが分かりました。③「あやめ」は陸上の乾燥地に自生しているのに対して、②「花菖蒲」と④「かきつばた」は日当たりのよい水辺や湿地に群生するのだそうです。
そういうことで、学校の北門へ続く上り坂の手前の道路際の花は、乾燥地にありましたので「あやめ」ということで一件落着。
剣状の細かい葉が縦に並んで茂る様子(これが文目(あやめ)模様に似ていることにその命名の由来があるということらしいです)がしっかりしたイメージを与え、花言葉も「良き便り」とか「希望」で前向きなこともあり、好きな花の一つです。
ところで、学校の横に所在する村山公園の別名は、「あやめ公園」なんだそうです。人吉市のHPの公園一覧のサイトにも「村山公園(あやめ公園)」の表記がありました。この記事を書くに当たり、どこにあやめ があるのだろうと、公園内をくまなく捜し回りました。「『ツツジ公園』と言ったほうがいいのでは?」と思うほど様々な色のツツジ*1が満開で、まさに百花繚乱の装いでしたが、あやめ はついに見つけることができず残念でした。でも、初夏を思わせる日差しの中、新緑が青空に映えて、最高に気持ちがよかったです。

「かきつばた」が出てくる第9段、校長室にあった国語便覧で改めて調べてみたらまさしく次のような話で、それを習った頃の教室の匂いまで懐かしくよみがえりました。
昔、ある男(=在原業平とおぼしき主人公)が都への未練を残しつつ関東の方への旅を続け、三河の八橋(今の愛知県知立市のあたり)に着いた。その沢のほとりの木蔭に馬から降りて座って、乾飯(かれいひ:水やお湯で戻して食べるドライライス)を食べた。
その沢に、かきつばたがとてもきれいに咲いていた。それを見てある人が、「かきつばたという五文字を各句の頭に置いて、旅の心情を詠みなさい」と言ったので、男が次のような歌を詠みます。
からごろも きつつなれにし つましあれば
はるばるきぬる たびをしぞおもふ
(現代語訳:着て馴れ親しんだような妻が都に居るものだから、はるばるとこんなに遠くまで来てしまった旅を悲しく思うのです)
最後に、乾飯の上にポロポロと涙が落ちて、乾飯はふやけてしまったのだった、という何とも切ない落ちまでつくという物語です。
このように、五七五七七のそれぞれの頭に、別の意味を持つ言葉を織り込む言葉遊びを「折句」と言います。この「かきつばた」の折句を伊勢物語で学習した際に、国語の先生が「クリスマスをお題にした折句の歌を作ってらっしゃい」と宿題にしたので、やってみたことがあります。
……ん~。………んっ!?……ん~ん。………はぁ
といった感じで、2~3時間格闘しましたが結局できませんでした。
俵万智さんの短歌集の中に一首、クリスマスの折句が紹介してあったことを思い出しました。田中章義さんという十代の歌人の予備校時代の作品で次の歌です。
クリスマス りんりん響く 鈴の音を 全く無視して スタディーハード
キーワードを隠すたわいもない言葉遊びのようですが、いざ作るとなるとそれがどうしてとても難しいのです。こういうのができる人はどのような才能を持っているのだろうと尊敬します。
国語の先生に伺ったところ、伊勢物語は2年生の2学期に学習し、第6段の「芥川」か、第23段の「筒井筒(つついづつ)」のどちらかを扱う予定だということでした。ネタバレになったらいけませんが、「筒井筒」は、井戸の周りで遊んでいた幼馴染のカップルが、大人になったら・・・?という、ちょっとビターな恋物語です。伊勢物語、きっと面白いです。是非、第9段の「かきつばた」も読んでみてください。
【校長】
*1ツツジは漢字で書くと「躑躅」となり、難読漢字になります。英語ではazaleaと綴り、カタカナでは「アゼリア」とか「アザレア」と表記します。阿蘇市にある「アゼリア21」というレジャー施設(阿蘇から流れる天然水を源泉としているプール)の名前を聞いたことがある人もいるかもしれません。ちなみに、アヤメは英語でirisと綴り、「アイリス」と表記されます。このiris、ギリシャ神話の「虹の女神」に由来する単語なんだそうです。
*2在原業平、今から約1,200年前に生きたこの方、天皇の血を引く由緒正しい実在の貴族なのですが、既存の風習にとらわれず、あちこちで女性と関係を持っていきます。そんな彼の女性遍歴集といっても過言ではないのがこの伊勢物語です。ついには神に仕える皇女と関係を持ってしまったのでは?ということを匂わせる話(第69段)もあります。関係を持った女性の数は何と3,733人!多分、誇張が入っているはずですが、今と結婚の形態が異なる平安時代の時代背景を考慮に入れても凄まじい数だと思います。実際にどれだけの女性と関係を持ったかは本人だけが知るところでしょうが、こうして物語のモデルとされてしまうくらいですから、女性関係が派手だったことは公然の事実だったのかもしれません。
575770 → 今は春べと 咲くやこの花♪
本日4月20日、午前9時37分現在のアクセス件数は、575770
最初の5桁、57577とは勿論、日本古来の三十一文字(みそひともじ)である和歌のことです。その後の0をどう解釈(こじづけるか)で悩みました。
0番目と捉えると、百人一首競技大会などで試合開始を告げる歌と考えてもいいのかな・・・と思いました。その歌は、百人一首には収められていませんが、スポーツの試合で開始を告げるホイッスルのように、百人一首競技の開始前に必ず詠まれるこの歌です。*1
難波津に 咲くやこの花 冬ごもり 今は春べと 咲くやこの花
【現代語訳】難波津(なにはづ)に、咲いたよこの花が。冬の間は籠っていて、今はもう春になったというわけで、咲いたよこの花が。
【解説】難波津とは、難波の港。難波は大阪市及びその付近の古称。第16代仁徳天皇*2が高津宮を置いた所です。この歌は、仁徳天皇が即位される時に、朝鮮(百済)からの渡来人の王仁博士(わにはかせ:生没年未詳)が、梅の花に添えて歌ったとされる歌です。陛下の治世が末永く続きますようにという願いを込めた、今でいう「君が代」みたいな祝福の歌です。
技巧などなく、見たままを素直に歌った和歌です。皆さん、実際に花が咲き乱れる様が目に浮かびますか?そういうことで、試合の開始時など印象的な場面で詠まれると、華やかな雰囲気が醸し出されますし、そういう効果を狙って詠まれているのかもしれません。
数年前、広瀬すずさんが主演して話題になった競技カルタの映画「ちはやふる」でもこの歌が詠まれるシーンが何度も出てきましたので、そう言えば・・・と記憶にある人もいるはずです。
日本が世界に誇る文化遺産ともいえる百人一首、小中学校でいくつか覚えたことがある人も多いことでしょうが、その成立事情は知っていますか?
平安末期~鎌倉初期の大歌人である藤原定家(ていかorさだいえ:1162~1241)が、友人から「100首の和歌を色紙にしてふすまに飾りたい。いい歌チョイスしてよ!」と頼まれ、飛鳥時代の第38代天智天皇から鎌倉時代の第84代順徳院まで、およそ450年間の中から100人の歌人の優れた和歌を一首ずつセレクトしたものです。まさに「藤原定家セレクション」といったところです。(このような異なる作者による詩文などの作品を集めたものを「アンソロジー(anthology)」と言いますが、これ、覚えておきたい言葉です)
文暦2年(1235年)の5月27日に、百人一首を完成させて、小倉山荘の障子に書写した和歌百首を貼ったという記録が、明月記(定家がつけていた日記)に残っていることから、5月27日は「百人一首の日」とされています。
今、巷(ちまた)では、俳句や川柳がとても盛んです。「良い句」と読める4月19日(昨日です!)や、5,7の並びにかこつけた5月7日に、年に1度の句会や総会などを行い、会員の親睦を深めている団体が多いようです。それにしても、575770とは、何とも堂々とした数字!これが達成された日は、和歌を話題にするしかないと考えていました。
実は・・・、4月当初の1日当たりの平均アクセス件数700件から見積もって、「百人一首の日」である5月27日前後にアクセス件数が575770になるのではという淡い期待のもと、この記事の構想を考えていました。そしたら、4月第2週目あたりから1日当たり1,500件とか2,000件、昨日などは4,000件を超えるアクセスを頂く日が続き、予想が大きく外れて早まってしまい、嬉しい悲鳴というか、ちょっと慌てて記事を作ったところでした。
ところで、定家の時代から900年近い歳月が流れ、三十一文字を現代では短歌と呼ぶようになり、歌の詠みぶりは随分変わってしまいました。私は初任校(高校教師になって一番最初に勤めた学校)で百人一首部の顧問を担当したことが縁で、すっかり和歌のとりこになってしまったのですが、和歌の普遍性についてつくづく考えることがあります。
一つは、歌は喜びを高らかに歌い上げることも多々ありますが、かなしみの器(うつわ)として用いられることが多いということです。そしてもう一つは、かなしむ人を美しいと思う日本人の感性です。歌の中に秘められた思いを想像し、共感して涙をもよおす心、これは感性がなせるものでしょうが、これもまた美しいと思っています。
手元のシラバスによると、本校では2年生の3学期の2月頃に国語(国語総合)で百人一首を学習するようです。「和歌」は古文ですから、現代に生きる私たちにはとっつきにくいところがあるのは否めません。でも考えてみてください。わずか三十一文字ですが、その中にあらゆる感情を打ち込んでくる力業ですので、そこに含まれる情報量はもの凄く多いです。ちょっと気のきいた人なら一つの和歌を題材にして小説がかけてしまう位の情報量といってもいいと思います。一つ一つが短編小説と言ってすら過言でありません。歌の中に秘められた思いを想像するうちに、好きな1首に出会えるように願っているところです。百人一首の授業をどうぞお楽しみに!
そして・・・、本校の三綱領の中に「好学」というのがあります。和歌と短歌の違い、俳句と川柳の違いなども、ぜひ興味をもって調べて知的好奇心を満たしてもらえればなお嬉しいです。 【校長】
*1競技百人一首では、競技のはじめに「序歌」という百首のいずれにも属さない特別枠の歌を詠みます。地方によって何の歌を詠むかは色々ありますが、競技百人一首の段位や公式ルールを仕切っている全日本かるた協会は、この「難波津の歌」を序歌に定めています。
*2仁徳天皇は、歴史上まれに見るほど、徳のある君主であり、その治世は何と87年間も続いたと「日本書紀」に記されています。特に、「かまどの煙」の逸話が有名です。
ある時仁徳天皇が高台から、民の家々を見ておられました。
しかし、かまどから煙が上がっている家がありませんでした。民が貧しい証拠です。
「これは租税が高すぎるのじゃ」
仁徳天皇は、3年間租税の徴収をやめ、労役を課すことをやめ、その間は宮殿の茅葺(かやぶき)も葺(ふ)きなおさず、雨漏りがしてもたらいで受けて、しのがれました。
3年後、ふたたび高台にのぼった仁徳天皇は、家々から元気よく煙が立ち上っているのを目にされます。「これでよし!」こうして3年ぶりに租税と労役をもとに戻しました。
このように徳の高い天皇のもとで国は栄えたということです。よって仁徳天皇のことを「聖帝(ひじりのみかど)」と呼ぶこともあります。「難波津の歌」は、そんな徳の高い仁徳天皇の御世が末永く続きますようにと、祝福をこめた寿(ことほ)ぎの歌です。
ところで、仁徳天皇のお墓を知っていますか?私が小学生の頃、大阪府堺市にある
堺市には3つの天皇陵が存在します。埋葬されている埴輪をよく調べてみたところ、学術上ここが仁徳天皇陵であると確定することは不可能であることにより、堺市大仙町に所在する古墳ということで、「大仙陵古墳」と称されているようです。自宅にあった「もう一度読む山川日本史」には、この古墳について「大仙陵古墳(伝仁徳陵)」と表記され、職員室にあった山川出版社の「高校日本史B」の教科書では、「大仙陵古墳(仁徳天皇陵)」と記載されていました。新しい史実に基づいて教科書が書き換えられるのはこれまでもあった話です。でもこの写真はきっと脳裏に焼き付いていることでしょう。
日本全国に20万基(古墳は1基、2基・・・と数えます)以上はあるといわれる古墳のなかで、日本最大の古墳であり、エジプトのクフ王のピラミッド、中国の秦の始皇帝陵と並ぶ世界3大墳墓の一つに数えられています。上から見ると円と四角を合体させた前方後円墳という日本独自の形で、5世紀中ごろに約20年をかけて築造されたと推定されているようです。
労役を課すことを中止するほど徳のある仁徳天皇が、そんなに歳月がかかる土木工事を民にさせたとは・・・と突っ込みを入れたくなる人もきっといるのでは?
565656とは何とまぁ!
4月15日(土)、午後6時5分前の本校
HPのアクセス件数は565656でした。
これを確認した時のスマホの右上に表示されていた電池残量が65%、丁度、おでん用に卵を6個茹でていた最中でした。この朱書きの数字を横に並べても565656、何という偶然だろうと思ってしまいました。
花に花言葉があるように、数字にも意味があると昔から信じられています。それによると、5には「変化が訪れる」、6には「富をもたらす」という暗示があり、その2つが組み合わさった56は「変化によって恩恵を授かる」と解されているようです。この56が3回順番に現れるとは、何とおめでたいことだろうと思い、この565656に関して、56に関する思い出を3つ綴ってみたいと思います。
ぱっと思いつくのは、本校が来年、創立56年目であるということ、第二次世界大戦の指導者だった山本五十六連合艦隊司令長官(「いそろく」:お父様が56歳だったときの子、「苦しいこともあるだろう/言いたいこともあるだろう/・・・の「男の修行」の名言で有名)、雷おこしの製作体験学習で、昔、修学旅行の時に引率したことがある東京浅草の雷5656会館、「シゴロク」や「高原のポニー」の愛称で親しまれたC56形蒸気機関車などです。
また、昭和56年(1981年)という切り口だったら、私が大学4年生の時でしたので、トヨタが高級スポーツ車「ソアラ」を販売してブームになったことや、ダイアナ妃がチャールズ王子と結婚したこと、作家の向田邦子さんが台湾で起こった航空機墜落事故で亡くなったことなど、当時の思い出に重ねながらいくつかはすぐに思きます。しかし、いずれも生徒の皆さんたちには生まれる前のことで関係ありませんよね。
そこで今日は、各クラスに配布されているシラバスを見ながら、皆さん方が高校3年間に学習することに関連付けて考えることにします。
最初の56です。2年生の国語総合で5月頃学習する「伊勢物語」に関連付けました。その心は、伊勢物語は第56代清和天皇(在位:946~967)の御代(みよ)の出来事だからです。まずクイズを1問。
千早(ちはや)ぶる 神代(かみよ)もきかず 龍田川(たつたがは)
からくれなゐに 水くくるとは
多分耳にしたことがある和歌だと思います。これは古今集に収録されており、百人一首にも採られ、数年前に公開されてヒットした競技かるたに青春を懸ける高校生の物語「ちはやふる」のタイトルにもなった超有名な歌です。現代語訳は不要でしょう。さて、誰の歌でしょう?
平安時代一のプレイボーイと名高く、光源氏のモデルの一人と言われ、「伊勢物語」の主人公のモデルとも考えられている人物…、そうです。在原業平(ありわらのなりひら)です。業平には清和天皇に関連してこんな悲恋があります。
清和天皇の后(きさき)となったのは藤原高子(たかいこ)。彼女は、清和天皇が17歳の時、25歳で入内(今でいう婚姻)し、貞明親王(後の陽成天皇)を産みました。高子は入内する前、業平と恋愛関係にあり、言うまでもなく高子の一族によって強引に別れさせられました。悲嘆に暮れる業平は、こんな歌を詠んでいます。
月やあらぬ 春や昔の 春ならぬ わが身ひとつは 元の身にして
【現代語訳】あの月は昔と変わったのだろうか。この梅の咲く春の景色は昔と変わっているのだろうか。いや、どちらもあなたと一緒に見上げた美しい月であるし、かぐわしい香りを楽しんだ梅の花である。しかし、あなたがいなくなり一人ぼっちになってしまった今、私の周りのものは何もかも変わってしまった気がする。私だけは元とのままで変わらないのに・・・
世の無常と手が届かない所に行ってしまった恋人に思いを馳せ、嘆いている歌ですが、日本和歌界に燦然と輝く最高傑作とも称され、外国の日本文学研究者によって他言語に翻訳されている数が最も多い和歌なんだそうです。
伊勢物語は全部で125段ですから、薄い文庫本1冊程度です。一話一話も短く、簡潔です。どこから読んでもいいし、読み飛ばしてもいいので疲れません。その意味で古典に親しむ入口として最適です。それでいて、深い内容があり、とても面白いです。何が、面白いのか?何と言っても、歌がいいです。現代人と変わらぬ喜怒哀楽を詠んでいますので、「この気持ち、わかるなぁ」と共感できる歌が必ず見つかるはずです。詠んでいる歌は、男女の恋愛、男同士の友情、親子の情愛、年を取ること、愛する人の死、旅の情緒など実に多彩です。ちなみに、先ほど紹介した「ちはやぶる」は第106段に、「月やあらぬ」は第4段にあります。1,2年生の皆さん、伊勢物語の学習、楽しみにしておいてください。
次の56は、3年生の数学Ⅱで就職試験対策として学習する場合の数(順列・組合せ:本来これらは数学Aで学習する内容です)に出てくる8C3の計算結果です。実は、8C3などは、本校入学後の6月に全科とも受験する計算技術検定の中でも出てきます。しかしその時は「詳しいことは数学で学ぶから、今は電卓操作だけできるようになりなさい!」などと言われ、意味は分からず、ひたすらキーを叩くことだけに没頭することになります。
8C3とは、8人の中から3人選ぶとき、何通りあるかということを計算する式で「Cの8,3」とか「コンビネーション8の3」とか読み、次の計算をします。
8C3=(8×7×6)/(3×2×1)=56通り
一般的には、n個の異なるものから順序を考えずにr個取り出す選び方をn個からr個取る「組合せ」といい、その総数をnCrであらわします。Cは組合せを意味するCombination(コンビネーション)の頭文字で、次の計算をします。
nCr=n!/(r!(n-r)!)になります。
(ここでn!=n・(n-1)・(n-2)・・・・・1です)
nとrの選び方で色々な計算結果が得られるわけですが、なぜ結果が56になる8C3を取り上げたかというと、その心は・・・。
昔、担任をしている時、「明日数学のテストというのに、数学の先生が帰っていて質問できません。先生、教えてくれませんか?」と言いながら、生徒が機械科の職員室に質問に来ました。見れば「男子3人、女子5人の中から3人を選ぶとき、男子が少なくとも1人含まれる選び方は何通りあるか」という問題です。
高校の頃、「順列・組合せ」はあまり得意なほうではなかったのですが、昔を思い出しながらどうにか教えました。このことが強く記憶に残っていたからです。答えは「46通り」です。皆さん分かりますか?
8人の中から3人選ぶのは、先ほど述べたとおり、
8C3=(8×7×6)/(3×2×1)=56通り
男子が少なくとも1人含まれるということは、3人とも女子の場合を引けばいいので、3人とも女子であるのは
5C3=(5×4)/(2×1)=10通り
従って、56-10=46通りになります。
数学では、「男子が少なくとも1人含まれる選び方」というのは、「全事象-女子が3人選ばれる選び方」で、これを「余事象」の考え方と言います。
実はこれ、ずっと昔の学生時代に大検(今は「高校卒業程度認定試験」と名称が変わっています)の試験監督をアルバイトでやっていたとき、全く同じ問題が出題されていたのを見たことも思い出しました。ということで、nとrの組み合わせは無数にあるのですが、市販の問題集や簡単な入試問題レベルでは8と3が多いような(あくまでも)気がして、結果の「56」というのは数学の先生の感性に訴える何かがあるからかな・・・?とか密かに思っているところです。
最後の56、これは何にこじつけようかな・・・と考えました。
憲法56条の定足数の内容、北緯56度や東経56度は地球上でどんな所を通っているか、第56代内閣総理大臣だった岸信介氏の頃の我が国の世相、原子番号56のBa(バリウム)の性質、在学中に皆さんが受験する電気工事士や危険物乙種第4類等の国家試験の中で56が超重要数字になっていなかったかな・・・と色々と調べてみましたが、ぱっとしたものはありませんでした。

その本にこの2つの鳥の生態が詳しくまとめてあり、こんなことが書いてあります。カワセミに関して、「宝石の翡翠(ひすい)は、このカワセミの名前から来ている。宝石のほうが先ではない。翡翠の二文字共に羽の字が入っていることからも判ろう」と。そしてヤマセミに関して、「産卵後56日で巣立つが、人吉市の観察では1日に1羽ずつ巣立っている」と。何と、ここに56という数字を偶然に見つけることができました!
皆さんも一日一度も数字を見ない日はないはずです。56という数字に注意を払って学校生活を送ってみましょう。
今日は長い文になってしまいました。ここまでお読みいただきありがとうございました。 【校長】
561248→172→All
入学式が終わって、更衣を済ませホッとしながら何気にHPを見たら、
午後3時10分現在のアクセス件数は、
561248
下4桁の1248とは、1<2<4<8で末広がりです。
「何と縁起がいいのだろう!」と思いながら、閃(ひらめ)くものがあ り まし た。
数字の並びをそのままにして、加減乗除の記号を入れてみます。
56+124―8=172
172とは、つい先ほど本校に入学した生徒数(本科168名、専攻科4名の計172名)です。私、「172って何てステキな数字だろう・・・」と「入学許可」の時、壇上にいながら思っていました。
というのも、各位の数を合計すると10*になるからです。「一を聞いて十を知る」「十人十色」のように、慣用表現では、10 は 「多く」「全部(All)」の比喩として使われています。たまたま時刻も3時10分、日付も4月10日ということで10が揃いました。10に比喩的に込められた「全部」にあやかって、172人全員が2年、あるいは3年後に揃って卒業できるようにと、この記事を書きながら願いを込めたところです。
同時に、様々な個性や能力を持った生徒たちが集まったこのダイヤモンドの原石の集団を、どう磨きどう輝かせて卒業させるか、私共の力の見せ所であり、責任を痛感するとともに、楽しみに思ったところでもあります。
【校長】
*【各位の数の和が10に関連して】
172は、各位の数の和が10となる17番目の数で、1つ前は163、次は181です。
各位の数の和が10というのは、数学の先生たちの人の関心を引くようで、2008年の入試では「2008は、各位の数字の和が10になる4桁の自然数である。このように、各位の数字の和が10になる4桁の自然数は全部でいくつあるか求めよ」といった問題がいくつか大学で出題されていました。
ちなみに今年、2017年も各位の数字の和が10で、2008年以来9年ぶりです。2008年の1つ前は何と「未成年者ハ煙草ヲ喫スルコトヲ得ス」で有名な未成年者喫煙禁止法が制定された1900年(明治33年)だったわけですから、数学の先生たちがいかに興奮したか容易に察しがつきます。そういうことで、さすがに今年は「2匹目のドジョウはいない」のかもしれませんが、生徒の皆さん、この問題に挑戦してみてはいかがでしょうか。(中学生の皆さんには結構手ごわいかもしれません。答えは219個です)
ところで、人の手の指の数は両指併せて10本です。多くの文明において標準的な記数法として十進法が採用されているのは、人間が指を折って数えるこの習慣から来ていると言われています。ちなみに、新入生の数172を16進数**で表すとACになります。
余談になりますが、ACというのは、電卓やパソコンの世界では、
All Clear(完全に消す)を意味します。入学してすぐ(6月頃)
受験する計算技術検定3級では、消すこと(ソロバンで言うとこ
ろの「御破算」)の重要性を嫌になるほど思い知るはずです。
直前に行った数値が残っていたら、正しい計算結果は出ませんよね。
きちんとクリアしてから計算を始めるようにすれば、おのずと間違
いは 少なくなります。だけどそれがクセになってしまって、一つの
数値の入力ミスでもAll Clearしてしまうと、特に長い計算式では再
入力の時間がもったいないです。皆さん方がこれから授業で使う電
卓は、入力ミスした部分だけを修正して要領よく計算ができるよう
な賢い電卓です。どうぞ、高校の専門の授業をお楽しみに!
**16進数は16を基数として表した数値です。高校入学後、全科で共通に学ぶ「情報技術基礎」(建築科と電気科は1年生で、機械科・建設工学科は2年生で学習)で、これまた嫌になるほど叩き込まれます。ちょっとだけ予習気分で・・・
16進数、ちょっと難しいですが、10進数と比較しながら考えたら分かりやすいかもしれません。10進数は、0から9までの 10種類の数字を使って数を表し、数が0から1、2、3…と順に増えていくとき、7、8、9 までは 1桁ですが、次は桁上がりして10になります。
同様に、16進数には16種類の数字があります。文字としての数字は0から9までの10種類しかないので、アルファベットのA~Fを「数字」として借用します。16進数は0からFまでの16種類の数字を使って数を表し、数が0から1、2、3… と順に増えていくとき、7、8、9の次はA、B、C と続き、D、E、F までは1桁ですが、次に桁上がりして10になります。コンピュータでは 2進数が使用されていますが、2進数は桁上がりが激しいので、例えば今話題にしている172だったら10101100となるように、大きな数値を2進数にすると桁数も多くなります。そこで16進数が登場するわけです。16進数にはアルファベットが混じったりするので、慣れないうちは「数」とは思いにくいかも知れませんが、0と1ばかりがやたら並んでいる 2進数よりは、はるかに扱い易いはずです。詳しいことは授業でのお楽しみということで、今日はこのへんで。
アクセス数555555件達成
いつも本校のHPにお越しいただきありがとうございます。
555555とは、4月2日(日)10時25分現在の本校のHPのアクセス件数です。前回のぞろ目である444444件を達成したのは、昨年11月5日(土)でした。従って、1日平均750件という県下の公立高校の中では最高水準のアクセスを日々いただきながら順調に数を増やし、148日(約5カ月)で111111件を積み上げて、555555件になったことになります。
次のぞろ目は666666ですが、その前に654321という記念すべき数字もあります。今の調子で順調に推移していくとすると、654321が8月11日(金)、666666が8月28日(月)で、いずれも夏休み期間中になりそうです。その頃どのような日々を送っているのか、考えるだけでも楽しいですね。「今年こそ宿題に追われない日でありたい」とか頭をよぎった人もいることでしょう?
ところで、555555という数字の並びは、高校の頃に因数分解同好会に所属していた私にとって妙に惹きたてられるものがあります。手始めに素因数分解をしてみました。
555555=3×5×7×11×13×37
でした。最初の素因数の並びが何とも綺麗です。従って、約数は 1, 3, 5, 7, 11, 13, 15, 21, 33, 35, ・・・・・(途中省略)・・・・・, 15873, 16835, 26455, 37037, 42735, 50505, 79365, 111111, 185185, 555555の64個あることになります。
そういえば、小学生の頃、「けけけけ555555 これな〜んだ?」というなぞなぞがあったことを思い出しました。生徒の皆さん分かりますか?
ヒントは「け◯5◯」です。(答え*はこの記事の最後に載せておきます)
ところで、ぞろ目はプレミアム(付加価値)が付くこともあります!

上の写真は、随分前ネットオークションで出品されていた発券番号P555555Xの5千円札です。最低落札希望価格が8万円だったのを覚えています。
5千円で思い出したのですが、生徒の皆さん、555,555円は英語で何と言うかは大丈夫ですか?世界共通の商慣習に従って3桁で区切りのコンマを入れていますが、まずコンマの前の数字は555です。千が555個という発想で、five hundred fifty five thousandとなり、次に555を同じようにと読んで追加します。従って、
five hundred fifty five thousand, five hundred(and) fifty-five yen
となります。英語の数字は、基本的にコンマごとに単位を変えて読めばいいので、一・十・百・千・万・・・・と、位どりがややこしい日本語の数字の読み方より簡単で合理的ですよね!
次のぞろ目である666666に向けて、HPの内容充実を図っていくつもりです。今後とも、本校のHPへのお越しをお待ち申し上げております。
【校長**】
*答え:「消しゴム」 これは、日本最大級のなぞなぞ問題集サイト(なぞQ.com)にも収録されていることを確認しました。それによると、5つの難易度レベル(ようちえん、かんたん、ふつう、むずかしい、おにころし)の中の「ふつう」レベルでした。このサイトの「おにころし」レベルの問題は、暇つぶしに十分楽しめますよ!
**このたびの定期人事異動で末廣克郎前校長の後任として天草工業高校から転任して参りました西智博と申します。天草工業高校もHPの充実に力を入れていましたが、どのようにすれば一日750件のアクセスが集まるのだろうと、球磨工業高校のHPをいつも尊敬の念で見ながら多方面から分析をしておりました。
今回、生徒たちが多方面で活躍し、全国にその名を轟かしている本校に赴任できたことを大変喜んでおりますし、赴任して何気に見たアクセス数をヒントにした本記事のアップが最初の仕事になりましたことを光栄に思います。HP運営者とともに魅力あるHPに力を入れて参りますので、今後とも宜しくお願いします。
球磨工の情報を発信中!
リンクはこちらから
学校情報
〒868‐8515
熊本県人吉市城本町800番地
TEL 0966-22-4189
FAX 0966-22-5049
E-mail
kuma-th@pref.kumamoto.lg.jp
熊本県教育情報システム
登録機関
管理責任者 校長 坂本道彦
運用担当者 ホームページ係