【学校からの連絡】
〇【高校入試】後期(一般)選抜における調査書及び成績一覧表の受付について
〇(在校生向け)大雨・台風・大雪等の緊急時の対応について
〇軽装勤務の通年実施について・・・熊本県では、働きやすい職場環境整備の観点から通年の軽装勤務を実施しており、本校でも奨励していますので御理解をお願いします。
〇令和7年度閉庁日についてはこちら →R7 学校閉庁日のお知らせ.pdf
【中2】二年生「18日の解答と新たな問題」
4月18日土曜日の解答と解説
第1問
答え:1ドルは消えていない。
この問題には、一見しただけで気づきづらい数字上の「ごまかし」が存在します。
「親友たちが1人9ドルを支払い、3人合計で27ドル支払ったことになる」という計算は合っています。
問題なのは「そこに受付係がくすねた2ドルを足して29ドル」という一文。
3人が払った27ドルというのは、正規の宿泊料25ドル + 受付係がくすねた2ドルを足したものです。
つまり、「27ドルに2ドルを足して29ドル」なのではなく、「27ドルから2ドルを引いた25ドルが親友も受付係も持っていないお金」と言うのが正しい文章です。
最後に、最終時点での30ドルの所有内訳を確認してみましょう。
親友3人:3ドル
受付係:2ドル
正規の宿泊料:25ドル
この通り、どこにも矛盾はありません。
「結果的なお金の流れ」と「実際に存在するお金」が同列に語られているからこそダマされやすい問題です。
第2問 解説しながら解答
まず、正解になりえる数字の組み合わせを書き出してみましょう。
0,0,9 0,1,8 0,2,7 0,3,6 0,4,5 1,1,7 1,2,6 1,3,5 1,4,4 2,2,5 2,3,4 3,3,3
以上の12個です。
この段階では、まだ誰も正解が分かりません。
しばらく時間が経過した時の状況
もし、正解の数字が(0,0,9)(0,1,8)(3,3,3)のいずれかであれば3人の生徒のうち誰かが即座にダイヤル錠を解除できます。しかし、そうはならなかった。
このことから、正解となる数字が(0,0,9)(0,1,8)(3,3,3)を除いた以下の9個にしぼりこまれます。
0,2,7 0,3,6 0,4,5 1,1,7 1,2,6 1,3,5 1,4,4 2,2,5 2,3,4
さて、この段階で生徒Bは正解にたどり着きました。
上記の組み合わせの数字の、2桁目に注目してください。
生徒Bの数字が「2」「3」「4」の場合、他にも選択肢があるので生徒Bは正解がわかりません。
しかし––生徒Bの数字が「1」の時のみ––生徒Bには正解が(1,1,7)だと分かります。
2桁目に「1」が登場する組み合わせ(0,1,8)が消えたことで、自身が「1」を持つ生徒Bは正解が(1,1,7)しか有りえないことを確信できるわけです。
そして生徒Bはダイヤル錠を解除して部屋から脱出します。
全員脱出へ
生徒Bがダイヤル錠を解除できたことを知った生徒Cは、これと同じ思考を辿ります。
生徒Bが脱出するまで、生徒Cの視点だと正解の選択肢は(0,2,7)(1,1,7)ですが、生徒Bが脱出できたことから正解は(1,1,7)でないと論理的にありえないことに気づき、生徒Cもダイヤル錠を解除できます。
同様に、生徒Aも基本骨子をトレースオンしてダイヤル錠を解除します。
めでたしめでたし
それでは新しい問題(みんなが解ける問題と思います)
第1問
ミカとサツキの2人がそれぞれ自分の馬に乗っている。
そこを通りかかった王様がこう言った。
「2人で馬に乗ってレースをしなさい。勝った馬の主の方に宝を与える。ただし、後でゴールした方を勝ちとする」
ミカとサツキは相手より先にゴールしないよう、のろのろとレースをしていた。
このままでは、いつまでも勝負がつかない。
だが、たまたま通りかかった賢者の一言を聞いた瞬間、2人はものすごい速度でゴールへ向かっていった。
いったい、賢者は何と言ったのだろうか?
第2問
仲間はずれの図形はどれ? 理由をつけて。答えましょう。
ブログアンケート“ 玉附Connection ”
みなさまのご意見、ご感想をお待ちしています!


 入学希望者の皆さんへ
入学希望者の皆さんへ 在校生・保護者の方
在校生・保護者の方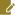 各種申し込み
各種申し込み アクセス
アクセス