【４月１８日（土）】　本日も仲山です
　みなさん元気にしてますか？　玉附ブログがすっかり楽しみの１つになりました。当初の予定では平日のみの更新でしたが、本日土曜日も更新させてもらいます。

　まずは、返信の中に私たちへのチャレンジがありましたので、さっそく解かせてもらいましたが、ぜひ皆さんにも解いてもらおうと思います。

　では、２年玉附人からの出題
「ＡとＢは、向かい合って同時に走り始めました。ＡとＢは、Ｃ地点ですれ違いました。Ｂは、その後、9分でＡがスタートした地点に着きました。また、Ａは、Ｂがスタートした地点にＣ地点から１分で着きました。この時、Ａは、Ｂの何倍の速度で進んでいましたか?」

＊解答、解説は来週のどこかで、多田隈先生がアップします。また、そのほかの問題についても解答や解説がアップされると思いますので、まだの人はチャレンジしてみましょう。

　

　次は、記事のリクエストに「先生たちの生活は？」とありましたので、書いてみます。

【NOBUのある１日】
　私は平日、基本的には学校で仕事をしています。生徒が用事で登校してくることもあるので、各学年の先生が誰か学校にいることにしています。私の場合は、ワークシートや授業で使うパワーポイントを作るのに、インターネット上の画像等を活用するので、家ではなかなかできません。昨日までは、みんなに配布した歴史プリント「人物編」の説明用教材をパワーポイントで作成していました。歴史が苦手な人のための振り返りにも役立つようにと考えています。復習したい人はどうぞというものです。
　

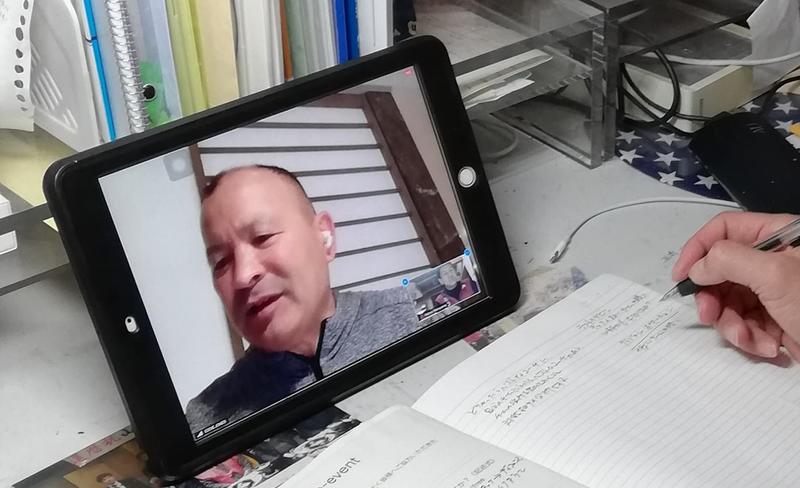
　昨夜は、【Ensemble Rugby Clinic 1 - ON ZOOM】というEddie Jones（元ラグビー日本代表監督、現イングランド代表監督）のオンラインセミナーに当選し、19：00～21：00までコーチングを学びました。

　今年はエディさんのClinicが開催されることはないだろうと諦めていましたが、こんなかたちでコーチングを学べるとは思ってもいなかったので、とても勉強になったし楽しかったです。また、このようなやり方で皆さんと繋がれたらいいなとも感じました。

 

　それでは、そろそろ今日の問題です。土日分で２問の出題です

第１問　論理クイズ「親友と消えた1ドル」

親友3人がホテルに泊まることになった。
宿泊料は1人10ドル。
親友たちは合計30ドルを受付係にわたした。
その後、キャンペーン中なので宿泊料は3人で25ドルだったことに気づいた受付係は、5ドルを返そうとした。
が、「5ドルは3人で割り切れない」と考えた受付係は2ドルを自分のポケットにしまい、残りの3ドルだけ親友たちに返金した。
さて、親友たちは1人9ドルで合計27ドル支払ったことになる。
そこに受付係がくすねた2ドルを足して29ドル。
残りの1ドルはどこに消えたのだろうか？

 

 

第２問論理クイズ「3人の生徒とダイヤル錠の部屋」

　劇場版名探偵コナン「ゼロの執行者」の公式ホームページで紹介された有名クイズ
ちょっと難しいですが、解けた時の爽快感は最上級。
　ぜひ時間をかけて取り組んでみてください。

「問題」
3人の生徒が豪（仮名）に閉じ込められた。
豪は生徒たちを別々の部屋に入れ、部屋の扉に3桁のダイヤル錠をかけた。
生徒たちは、30分以内にダイヤル錠を解除して部屋から脱出しなければならない。
豪は生徒たちに以下のことを告げた。

• すべてのダイヤル錠は、共通の数字で解除できる
• 正解となる数字は「000〜999」のいずれかである
• 3桁の数字を合計すると9になる
• すべての桁の数字が、左の桁の数字以上の数字である
• 一番左の桁を「1桁目」とした時、生徒Aには1桁目を、生徒Bには2桁目を、生徒Cには3桁目を教えた

生徒たちは、いかなるコミュニケーションも取ることもできない。
ただし、「いつ誰がダイヤル錠を解除したか」はリアルタイムで知ることができる。
当初、生徒たちは誰もダイヤル錠を解除できなかった。
ところが、しばらくして誰も解除できなかったのを知った生徒Bは、「正解の数字」が分かりダイヤル錠を解除した。

続いて、それを知った生徒Cがダイヤル錠を解除した。

最後に、2人の様子を知った生徒Aがダイヤル錠を解除した。

いったい、正解の数字は何だったのだろうか？
なお、3人の生徒はいずれも極めて論理的な思考を行うものとする。

＊一見すると難解ですが、意外と地道な方法で正解にたどり着けるかもしれません。

以下は「問題のポイント」
生徒たちの部屋にかけられたダイヤル錠の「正解の数字」は、いずれも同じです。
まず、「3桁の数字を合計すると9になる」というのが大きなポイントです。

名探偵コナンをBGMに解いてみましょう。

楽しんでください。

 

ブログアンケート“玉附Connection”

みなさまのご意見、ご感想をお待ちしています！